Урок-тренинг по геометрии в 9 классе «Решение планиметрических задач по теме «Окружность и круг» из открытого банка заданий ОГЭ »

Урок-тренинг по геометрии в 9 классе

«Решение планиметрических задач по теме «Окружность и круг» из открытого банка заданий ОГЭ »

Цели и задачи урока:

Образовательная: Систематизировать знания учащихся по ключевым разделам планиметрии. Создать содержательные и организационные условия для применения школьниками комплекса знаний для решения задач, включаемых в материалы ГИА.

Развивающая: Развивать личностно-смысловые отношения учащихся к изучаемому предмету. Способствовать формированию коллективной и самостоятельной работы, формировать умение четко и ясно излагать свои мысли.

Воспитательная: Развитие памяти, внимания, логического мышления, наблюдательности. Развитие способности обобщать, классифицировать. Развитие самоконтроля.

Тип урока: повторения, обобщения и систематизации знаний.

Технологии: ИКТ - технология, дифференцированного обучения.

Оборудование: проектор, экран, компьютер, презентация Power Point, карточки с заданиями.

Сценарий урока

1. Приветствие

Вхожу в класс и читаю:

Нет, не всегда смешон и узок

Мудрец, глухой к делам земли:

Уже на рейде в Сиракузах

Стояли римлян корабли.

Над математиком курчавым

Солдат занес короткий нож,

А он на отмели песчаной

Окружность вписывал в чертеж.

Ах, если б смерть — лихую гостью —

Мне так же встретить повезло,

Как Архимед, чертивший тростью

В минуту гибели — число!

Приветствую вас, дорогие друзья и уважаемые коллеги. Наверняка вы уже догадались, что говорить мы сегодня будем опять об окружности. Мы заканчиваем изучать главу «Правильные многоугольники», а именно в этой главе рассматриваются длина окружности и площадь круга. В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Неслучайно наверно и символом олимпиады являются пять колец, пять окружностей. Я не просто так вспомнила олимпийский символ, ведь сейчас проходят главные соревнования для спортсменов всего мира – олимпийские игры. А что нужно спортсмену для удачного выступления? Много тренироваться. И нам, чтобы успешно сдать экзамены нужно много тренироваться. А чтобы тренировки прошли более успешно начнем с разминки.

1. Актуализация знаний.

Задания на экзамене предлагаются каждый год разные. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. Кроме того, в экзаменационной работе есть задание № 20, проверяющее, как ученик ориентируется в теоретическом материале. В каждом варианте в задании №20 предлагается по три вопроса, и надо из них выбрать либо верные утверждения, либо неверные. Иногда из-за одного пропущенного слова меняется смысл сказанного. Поэтому мы начнём наш тренинг с проверки знания теории.

1. Решение задач 1 части модуля «Геометрия».

Что успешно сдать экзамен, нужно решить не менее 2 заданий из модуля «Геометрия». Рассмотрим несколько задач устно.

Работа по готовым чертежам. (Слайды, раздаточный материал)

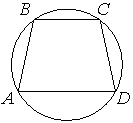
Задача 1. (слайд) Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах

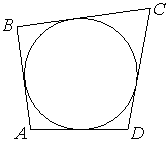
Задача 2. (слайд) Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD

Задача 3. (слайд) Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах

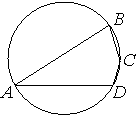
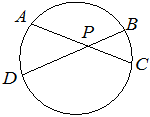
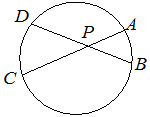
Задача 4. (слайд) Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP

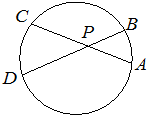
На ваших столах карточки с задачами. Разбираем, решение записываем у доски.

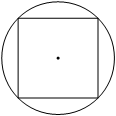
Задача 1 Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата
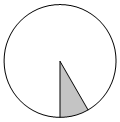
Задача 2. Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30
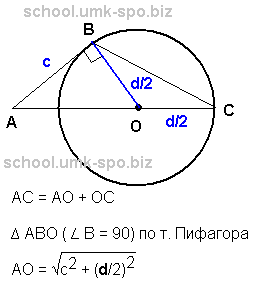
Задача 3. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Задача 4 . В треугольнике ABC угол C равен 30°, AB=16. Найдите радиус окружности, описанной около этого треугольника.
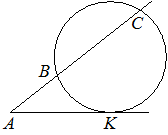
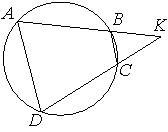
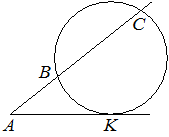
Задача 5.Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, AC=12. Найдите AK.
Задача 6. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=72, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.	Окружности радиусов 36 и 45 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

1. Пауза. Интересные сведения по теме урока

Круг и окружность в природе, повседневной жизни, в стихах

Одно из самых таинственных мест в Германии – Гозейский круг, памятник, сделанный из земли, гравия и деревянных палисадов, который считается самым ранним примером примитивной “солнечной обсерватории.” Круг состоит из ряда круглых канав, окруженных стенами палисада (которые были с тех пор восстановлены). Считается, что памятник был построен приблизительно в 4900 году до н.э. Неолитическими народами.

Световые явления в природе. Круговорот воды в природе

Фотография ночного неба

Зодиакальный круг

Волшебные круги

Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль 

1. Применение полученных знаний при решении задач. Дифференцированная работа (минут 15)

Класс делится на две группы.

Группа высокомотивированных: Двое сильных учащихся представляют решение задач из второй части модуля «Геометрия» на доске. Остальные слушают. Записывают.

На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=72, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.

Окружности радиусов 36 и 45 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Группа средних учащихся: решают задачи 1 части модуля «Геометрия» самостоятельно подобные тем, которые разбирались в классе, я прохожу, смотрю, подсказываю.

1 вариант	2 вариант
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.	Сторона квадрата равна 62. Найдите радиус окружности, вписанной в этот квадрат.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 53°. Найдите угол C этой трапеции. Ответ дайте в градусах.	Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 79°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, AC=8. Найдите AK.	Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, AC=12. Найдите AK.
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP	Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP

1. Итог урока.

Вот и подходит к концу наш урок и надеюсь, что он прошел не зря. Все задания, представленные сегодня на уроке из открытого банка заданий ОГЭ. Напоследок хотелось сказать, если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работ. Ведь, по словам Платона, способный к математике изощрен во всех науках в природе.

1. Домашнее задание. По группам (сильные решают задачи из второй части, остальные – карточки)