Пояснительная записка
Рабочая программа по геометрии составлена:
- на основе федерального компонента государственного стандарта среднего (полного) общего образования,
- примерной программы по математике основного общего образования,
- авторской программы «Геометрия, 10 – 11», авт. Л.С. Атанасян и др.,
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2013-2014 учебный год,
с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся 11 класса средствами данного учебного предмета.
Организационно-планирующая функция предусматривает структурирование учебного материала, определение его количественных и качественных характеристик.
Данная рабочая программа, тем самым содействует сохранению единого образовательного пространства, не сковывая творческой инициативы учителей, предоставляет широкие возможности для реализации различных подходов к построению учебного курса.
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжается и получает развитие содержательная линия: «Геометрия». В рамках указанной содержательной линии решаются следующие задачи:
-изучение свойств пространственных тел,
- формирование умения применять полученные знания для решения практических задач.
Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Обще учебные умения, навыки и способы деятельности
В ходе освоения содержания геометрического образования, учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
-построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
-выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале;
- выполнения расчетов практического характера;
-использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
-самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
-проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
-самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения геометрии на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
уметь
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
СОДЕРЖАНИЕ КУРСА
Координаты и векторы. Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Длина вектора в координатах, угол между векторами в координатах. Коллинеарные векторы, коллинеарность векторов в координатах.
Тела и поверхности вращения. Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей. Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Календарно- тематическое планирование
по геометрии 11 класса
2 часа в неделю, всего- 68 часов
| № урока | Содержание (тема урока) | Кол-во часов | Дата проведения | Контроль | Используемые ресурсы | Примечание | ||||||
| план | факт | |||||||||||
| Глава 4
|
|
|
|
|
| |||||||
| 1 | Понятие вектора пространстве | 1 |
|
|
|
| ||||||
| 2 | Сложение и вычитание векторов. Умножение вектора на число | 1 |
| диктант | тест |
| ||||||
| 3 | Сложение и вычитание векторов. Умножение вектора на число | 1 |
| с/р | карточки |
| ||||||
| 4 | Компланарные векторы | 1 |
|
|
|
| ||||||
| 5 | Компланарные векторы | 1 |
| диктант | тест |
| ||||||
| 6 | Решение задач | 1 |
| с/р | карточки |
| ||||||
| Глава 5 Метод координат в пространстве | 15 |
|
|
|
| |||||||
| 7 | Координаты точки и координаты вектора | 1 |
|
|
|
| ||||||
| 8 | Координаты точки и координаты вектора | 1 |
| диктант | тест |
| ||||||
| 9 | Координаты точки и координаты вектора | 1 |
| с/р | карточки |
| ||||||
| 10 | Координаты точки и координаты вектора | 1 |
|
|
|
| ||||||
| 11 | Координаты точки и координаты вектора | 1 |
| диктант | тест |
| ||||||
| 12 | Координаты точки и координаты вектора | 1 |
| с/р | карточки |
| ||||||
| 13 | Скалярное произведение векторов | 1 |
|
|
|
| ||||||
| 14 | Скалярное произведение векторов | 1 |
| диктант | тест |
| ||||||
| 15 | Скалярное произведение векторов | 1 |
| с/р | карточки |
| ||||||
| 16 | Скалярное произведение векторов | 1 |
|
|
|
| ||||||
| 17 | Скалярное произведение векторов | 1 |
|
|
|
| ||||||
| 18 | Скалярное произведение векторов | 1 |
| диктант | тест |
| ||||||
| 19 | Скалярное произведение векторов | 1 |
| с/р | карточки |
| ||||||
| 20 | Контрольная работа № 1 | 1 |
| к/р | карточки |
| ||||||
| 21 | Решение задач | 1 |
|
|
|
| ||||||
| Глава 6 Цилиндр. Конус, шар | 16 |
|
|
|
| |||||||
| 22 | Цилиндр | 1 |
|
|
|
| ||||||
| 23 | Цилиндр | 1 |
| диктант | тест |
| ||||||
| 24 | Цилиндр | 1 |
| с/р | карточки |
| ||||||
| 25 | Конус | 1 |
|
|
|
| ||||||
| 26 | Конус | 1 |
| диктант | тест |
| ||||||
| 27 | Конус | 1 |
| с/р | карточки |
| ||||||
| 28 | Конус | 1 |
|
|
|
| ||||||
| 29 | Сфера | 1 |
|
|
|
| ||||||
| 30 | Сфера | 1 |
| диктант | тест |
| ||||||
| 31 | Сфера | 1 |
| с/р | карточки |
| ||||||
| 32 | Сфера | 1 |
|
|
|
| ||||||
| 33 | Сфера | 1 |
| диктант | тест |
| ||||||
| 34 | Сфера | 1 |
| с/р | карточки |
| ||||||
| 35 | Сфера | 1 |
|
|
|
| ||||||
| 36 | Контрольная работа № 2 | 1 |
| к/р | карточки |
| ||||||
| 37 | Решение задач | 1 |
|
|
|
| ||||||
| Глава 7 Объемы тел | 17 |
|
|
|
| |||||||
| 38 | Объем прямоугольного параллелепипеда | 1 |
|
|
|
| ||||||
| 39 | Объем прямоугольного параллелепипеда | 1 |
| диктант | тест |
| ||||||
| 40 | Объем прямоугольного параллелепипеда | 1 |
| с/р | карточки |
| ||||||
| 41 | Объем прямой призмы и цилиндра | 1 |
|
|
|
| ||||||
| 42 | Объем прямой призмы и цилиндра | 1 |
| диктант | тест |
| ||||||
| 43 | Объем наклонной призмы, пирамиды, конуса | 1 |
| с/р | карточки |
| ||||||
| 44 | Объем наклонной призмы, пирамиды, конуса | 1 |
|
|
|
| ||||||
| 45 | Объем наклонной призмы, пирамиды, конуса | 1 |
| диктант | тест |
| ||||||
| 46 | Объем наклонной призмы, пирамиды, конуса | 1 |
| с/р | карточки |
| ||||||
| 47 | Объем наклонной призмы, пирамиды, конуса | 1 |
|
|
|
| ||||||
| 48 | Объем шара и площадь сферы | 1 |
|
|
|
| ||||||
| 49 | Объем шара и площадь сферы | 1 |
| диктант | тест |
| ||||||
| 50 | Объем шара и площадь сферы | 1 |
| с/р | карточки |
| ||||||
| 51 | Объем шара и площадь сферы | 1 |
|
|
|
| ||||||
| 52 | Объем шара и площадь сферы | 1 |
|
|
|
| ||||||
| 53 | Контрольная работа № 3 | 1 |
| к/р | карточки |
| ||||||
| 54 | Решение задач | 1 |
|
|
|
| ||||||
| Обобщающее повторение | 14 |
|
|
|
| |||||||
| 55 | Задачи по планиметрии | 1 |
| диктант | тест |
| ||||||
| 56 | Задачи по планиметрии | 1 |
| с/р | карточки |
| ||||||
| 57 | Задачи по планиметрии | 1 |
| диктант | тест |
| ||||||
| 58 | Задачи по планиметрии | 1 |
| с/р | карточки |
| ||||||
| 59 | Площади поверхности многогранников | 1 |
| диктант | тест |
| ||||||
| 60 | Площади поверхности многогранников | 1 |
| с/р | карточки |
| ||||||
| 61 | Площади поверхности тел вращения | 1 |
| диктант | тест |
| ||||||
| 62 | Площади поверхности тел вращения | 1 |
| с/р | карточки |
| ||||||
| 63 | Объемы | 1 |
| диктант | тест |
| ||||||
| 64 | Объемы | 1 |
| с/р | карточки |
| ||||||
| 65 | Векторы | 1 |
| диктант | тест |
| ||||||
| 66 | Векторы | 1 |
| с/р | карточки |
| ||||||
| 67 | Векторы | 1 |
|
|
|
| ||||||
| 68 | Заключительный урок | 1 |
|
|
|
| ||||||
Контрольные работы 11 класса
Контрольная работа № 1
по теме «Координаты точки и координаты вектора»
Вариант 1
Найдите координаты вектора
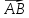 , если А (5; —1; 3), В (2; —2; 4).
, если А (5; —1; 3), В (2; —2; 4).Даны векторы
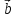 {3; 1; —2} и
{3; 1; —2} и 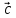 {1; 4; —3}. Найдите 2
{1; 4; —3}. Найдите 2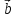 —
— 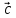 .
.Изобразите систему координат O xyz и постройте точку A (1; —2; -4).
Найдите расстояние от этой точки до координатных плоскостей.
Вариант 2
Найдите координаты вектора
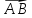 , если А (6; 3; —2), В (2; 4; —5)
, если А (6; 3; —2), В (2; 4; —5)Даны векторы
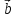 {5; -1; 2} и
{5; -1; 2} и 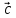 {3; 2; -4}. Найдите
{3; 2; -4}. Найдите 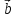 — 2
— 2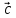 .
.Изобразите систему координат Oxyz и постройте точку А (—2; —3; 4).
Найдите расстояние от этой точки до координатных плоскостей.
Контрольная работа № 2
по теме «Метод координат в пространстве»
Вариант 1
Даны точки P (1; 0; 2), H (1;
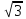 ; 3), К (-1; 0; 3), M (— 1; — 1; 3). Найдите угол между векторами
; 3), К (-1; 0; 3), M (— 1; — 1; 3). Найдите угол между векторами 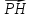 и
и 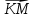
Найдите скалярное произведение
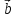 (
(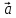 — 2
— 2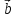 ), если |
), если | 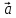 | =2, |
| =2, | 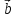 | = 4. а угол между векторами
| = 4. а угол между векторами 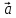 и
и 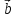 равен 135°
равен 135°Длина ребра куба ABCDA1B1C1D1 равна 2а, точка Р — середина отрезка ВС. Найдите:
а) расстояние между серединами отрезков B1D и АР;
б) угол между прямыми B1D и АР
4. Дан вектор 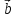 {0;-2; 0}. Найдите множество точек M, для которых
{0;-2; 0}. Найдите множество точек M, для которых 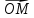 ∙
∙ 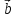 = 0, если О — начало координат.
= 0, если О — начало координат.
Вариант 2
Даны точки E (2; 0; 1), M (3;
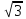 ; 1), F(3;0; -1), К(3; - 1; - 1). Найдите угол между векторами
; 1), F(3;0; -1), К(3; - 1; - 1). Найдите угол между векторами 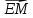 и
и 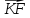 .
.Найдите скалярное произведение
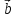 (
(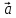 +
+ 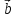 ), если |
), если | 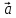 | =3, |
| =3, | 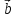 | = 2, а угол между векторами
| = 2, а угол между векторами 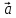 и
и 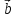 равен 150
равен 150Длина ребра куба ЛABCDA1B1C1D1равна 4а, точка P — середина отрезка DC. Найдите:
а) расстояние между серединами отрезков A1С и АР;
б) угол между прямыми A1С и АР.
4. Дан вектор 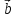 {0; 0; —5}. Найдите множество точек М, для которых
{0; 0; —5}. Найдите множество точек М, для которых 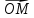 ∙
∙ 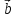 = 0, если О — начало координат
= 0, если О — начало координат
Контрольная работа № 3
по теме «Цилиндр, конус и шар»
Вариант 1
Осевое сечение цилиндра - квадрат, площадь основания цилиндра равна 16 см2. Найдите площадь полной поверхности цилиндра
Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30°;
б) площадь боковой поверхности конуса
3. Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы этой плоскостью.
Вариант 2
Осевое сечение цилиндра — квадрат, диагональ которого равна 4 см. Найдите площадь полной поверхности цилиндра
Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60е;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 4
по теме «Объемы тел»
Вариант 1
В правильной треугольной пирамиде боковые ребра наклонены к основанию под углом 60°, длина бокового ребра 8 см. Найдите объем пирамиды.
В конусе через его вершину под углом φ к плоскости основания проведена плоскость, отсекающая от окружности дугу в 2. Радиус основания конуса равен R. Найдите объем конуса.
В пирамиде из задачи 1 найдите расстояние между ребрами, лежащими на скрещивающихся прямых
Вариант 2
В правильной треугольной пирамиде плоский угол при вершине равен 60°, длина бокового ребра 4 см. Найдите объем пирамиды.
В конусе через его вершину под углом φ к плоскости основания проведена плоскость, отсекающая от окружности основания дугу в . Высота конуса равна h. Найдите объем конуса.
3. В пирамиде из задачи 1 найдите расстояние между скрещивающимися ребрами.
Контрольная работа № 5
по теме «Объем шара и площадь сферы»
Вариант 1
На расстоянии 8 см от центра шара проведено сечение, диаметр которого равен 12 см. Найдите площадь поверхности и объем шара.
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 60°. Найдите отношение объемов конуса и шара.
Объем цилиндра равен 96 см2, площадь его осевого сечения равна 48 см2. Найдите площадь сферы, описанной около цилиндра.
Вариант 2
Диаметр сечения шара, удаленного от центра шара на 12 см, равен 10 см. Найдите площадь поверхности и объем шара.
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 30°. Найдите отношение объемов конуса и шара.
Диаметр шара равен высоте цилиндра, осевое сечение которого квадрат. Найдите отношение объемов цилиндра и шара
Контрольная работа 6 (итоговая)
Вариант 1
В правильной четырехугольной пирамиде MABCD сторона основания равна 6, а боковое ребро — 5. Найдите:
а) площадь боковой поверхности пирамиды;
б) объем пирамиды;
в) угол наклона боковой грани к плоскости основания;
г) скалярное произведение векторов (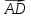 +
+ 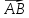 ) ∙
) ∙ 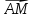 ;
;
д) площадь описанной около пирамиды сферы;
е) угол между BD и плоскостью DMC.
Вариант 2
В правильной четырехугольной пирамиде MABCD боковое ребро равно 5 и наклонено к плоскости основания под углом 60°. Найдите:
а) площадь боковой поверхности пирамиды;
б) объем пирамиды;
в) угол между противоположными боковыми гранями;
г) скалярное произведение векторов (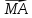 +
+ 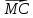 ) ∙
) ∙ 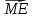 ;
;
д) площадь описанной около пирамиды сферы;
е) угол между боковым ребром AM и плоскостью DMC.

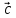 {1; 4; —3}. Найдите 2
{1; 4; —3}. Найдите 2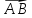 , если А (6; 3; —2), В (2; 4; —5)
, если А (6; 3; —2), В (2; 4; —5)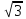 ; 3), К (-1; 0; 3),
; 3), К (-1; 0; 3), 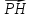 и
и 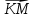
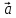 — 2
— 2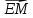 и
и 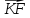 .
.



