Рабочая программа по математике 10 класс базовый уровень

Муниципальное бюджетное общеобразовательное учреждение

«СОШ п. Эгвекинот»

УТВЕРЖДАЮ

Директор МБОУ « СОШ п. Эгвекинот Приказ № от «30» августа 2017г. ___________ Н. С. Голохвастова

Рабочая программа

по математике 10 класс

базовый уровень

170 часов

на 2017-2018 учебный год

Составитель программы: Трушакова Светлана Алексеевна

П. Эгвекинот

2017г

2. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Настоящая программа по алгебре и началам математического анализа для 10 класса (базовый уровень) составлена на основе Федерального компонента государственного стандарта среднего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерной программы для общеобразовательных учреждений по алгебре и началам математического анализа к УМК «Алгебра - 10 класс. Базовый уровень - автор Алимов Ш. А.» [Программы для общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы. Авторы-составители И.И.Зубарева, А.Г.Мордкович – М.: Мнемозина, 2009.] Программа составлена на основе Программы для общеобразовательных учреждений по алгебре для 10 - 11 классов.

УМК «Алгебра - 10 класс. Базовый уровень» - автор Алимов Ш. А

УМК «Геометрия 10-11класс. Автор Л.С. Атанасян, В.Ф.Бутузов »

Планирование по геометрии составлено на основе программы по математике для общеобразовательных школ, лицеев, гимназий. Издательство «Дрофа» М- 2002 г., автор Кузнецова Г.М., с учетом тематического планирования по геометрии 10 класса, автор В.А.Яровенко. М.:ВАКО,2006 г. Рабочие программы по геометрии: 7-11 классы/Сост. Н.Ф.Гаврилова. –М .:ВАКО, 2011. Учебник: Л.С.Атанасян, В.Ф.Бутузов. Геометрия 10-11 класс. М.: Просвещение,2008 г

Общая характеристика курса

При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».

В рамках указанных содержательных линий решаются следующие задачи:

систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;

расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;

развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.

Цели и задачи обучения математике

Главной целью школьного образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: учеба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.

Целью прохождения настоящего курса является:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

В ходе ее достижения решаются задачи:

1) систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;

2) расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;

3) знакомство с основными идеями и методами математического анализа.

Рабочая программа учебного курса составлена на основе Примерной программы среднего (полного) общего образования по математике в соответствии с федеральным компонентом государственного стандарта и с учетом рекомендаций авторских программ А.Г.Модковича по алгебре и началам анализа и Л.С.Атанасяна по геометрии.

Согласно базисному учебному плану гимназии, рекомендациям Министерства образования Российской Федерации и в продолжение начатой в средней школе линии, выбрана данная учебная программа и учебно-методический комплект.

В соответствие с базисным учебным планом и с учетом направленности класса на изучение математики на базовом уровне в 10 классе отводится 5 часов в неделю.

Курс математики 10 класса состоит из следующих предметов: «Алгебра и начала анализа», «Геометрия», «Элементы логики, комбинаторики, статистики и теории вероятности», которые изучаются блоками. В соответствии с этим составлено тематическое планирование: алгебра и начала анализа из расчета 3 часа в неделю, геометрия – 2 часа в неделю. Тематическое планирование составлено на 170 часов.

Контрольных работ за год – 13, одна из них итоговая, по алгебре и началам анализа 8 работ, по геометрии 4 работ.

Используемые технологии, методы и формы работы.

Основная форма организации образовательного процесса – классно-урочная система.

Предусматривается применение следующих технологий обучения:

1. традиционная классно-урочная

2. игровые технологии

3. элементы проблемного обучения

4. технологии уровневой дифференциации

5. здоровьесберегающие технологии

6. ИКТ

Виды и формы контроля: промежуточный, предупредительный контроль; контрольные работы.

Методы обучения

1. Классификация по источнику знаний:

   • Словесные

   • Наглядные

   • Практические

2. Классификация по характеру УПД

   • Объяснительно-иллюстративный

   • Проблемное изложение знаний

   • Частично-поисковый (эвристический)

   • Исследовательский

   • Репродуктивный

3. Классификация по логике

   • Индуктивный

   • Дедуктивный

   • Аналогии

Для продуктивной работы по данной программе следует сочетать многообразие методов обучения.

Формы работы.

К наиболее приемлемым формам организации учебных занятий по математике можно отнести:

Урок-лекция. Предполагаются  совместные усилия учителя и учеников для решения общей проблемной познавательной задачи.

Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования,  решение различных задач, практическое применение различных методов решения задач. Комбинированный урок предполагает выполнение работ и заданий разного вида.

Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.

Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования.

Урок - самостоятельная работа.  Предлагаются разные виды самостоятельных работ.

Урок - контрольная работа. Контроль знаний по пройденной теме.

Урок-зачет. Проверка теоретического материала.

График контрольных работ

	Алгебра и начала анализа		Геометрия
№ К/р	Тема	Дата проведения	Тема	Дата проведения
1	«Числовые функции»		«Параллельность прямых и плоскостей»
2	«Определение тригонометрических функций»		«Параллельность плоскостей. Тетраэдр и параллелепипед»
3	«Свойства и графики тригонометрических функций»		«Перпендикулярность прямых и плоскостей».
4	«Тригонометрические уравнения»		«Многогранники»
5	«Преобразование тригонометрических выражений»
6	«Вычисление производных»
7	«Применение производной к исследованию функций»
8	«Применение производной»
	Итоговая контрольная работа.

3.МИНИМУМ СОДЕРЖАНИЯ ОБРАЗОВАНИЯ

Алгебра и начала анализа	Геометрия
Разделы программы
Глава 1. Числовые функции.	Аксиомы стереометрии и их следствия
Глава 2. Тригонометрические функции.	Глава 1. Параллельность прямых и плоскостей
Глава 3. Тригонометрические уравнения.	Глава 2. Перпендикулярность прямых и плоскостей
Глава 4. Преобразование тригонометрических выражений.	Глава 3. Многогранники
Глава 5. Производная.	Глава 4. Векторы в пространстве.

4. СОДЕРЖАНИЕ ПРЕДМЕТА

Алгебра и начала анализа

Разделы программы	Всего часов	Контрольная работа	Понятия
Глава 1. Числовые функции.	5	-	Понятие функции. Область определения и область значений функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, ограниченность функции, непрерывность. Четные и нечетные функции. Обратная функция.
Глава 2. Тригонометрические функции.	26	3	Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса углов. Основные тригонометрические формулы. Тригонометрические тождества. Тригонометрические функции
Глава 3. Тригонометрические уравнения.	11	1	Тригонометрические уравнения   sinx=a, cosx=a, tgx=a, сtgx=a. Решение тригонометрических уравнений. Простейшие тригонометрические неравенства.
Глава 4. Преобразование тригонометрических выражений.	15	1	Синус, косинус, тангенс и котангенс суммы и разности аргументов. Синус, косинус, тангенс и котангенс двойного угла. Сумма и разность синусов, косинусов, тангенсов и котангенсов.        Преобразования простейших тригонометрических выражений
Глава 5. Производная.	34	3	Понятие о пределе и непрерывности функции. Понятие производной. Производная степенной функции. Производная суммы, произведения и частного двух функций. Производные тригонометрических функций.
Повторение. Итоговая контрольная работа	11	1	Основные тригонометрические формулы. Тригонометрические функции Основные свойства функций. Решение тригонометрических уравнений. Простейшие тригонометрические неравенства. Понятие производной. Производная степенной функции. Правила дифференцирования. Производные тригонометрических функций. Понятие о пределе и непрерывности функции. Механический и геометрический смысл производной. Исследование функций, построение их графикой с помощью производной.
Итого:	102	9	Тригонометрические функции. Тригонометрические уравнения. Преобразование тригонометрических выражений Производная.

Геометрия

Разделы программы	Всего часов	Контрольная работа	Понятия
Аксиомы стереометрии и их следствия	5	-	Основные понятия стереометрии (точка, прямая, плоскость, пространство).
Глава 1. Параллельность прямых и плоскостей	19	2	Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве. Взаимное расположение прямых в пространстве. Параллельность плоскостей. Тетраэдр и параллелепипед.
Глава 2. Перпендикулярность прямых и плоскостей	20	1	Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Параллельное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур.
Глава 3. Многогранники	12	1	Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Глава 4. Векторы в пространстве.	6	-	Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение по трем некомпланарным векторам.
Повторение	6		Параллельность прямых и плоскостей. Перпендикулярность прямых и плоскостей. Многогранники.
Итого	68		Параллельность прямых и плоскостей. Перпендикулярность прямых и плоскостей. Многогранники.

5. КРИТЕРИИ ОЦЕНКИ

Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

- допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Оценка устных ответов обучающихся по математике.

Ответ оценивается отметкой «5», если ученик:

- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

-продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

-отвечал самостоятельно, без наводящих вопросов учителя;

- возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

- допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

- имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

обнаружено незнание учеником большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

- незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

- нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

6.ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ

Требования к уровню математической подготовки задаются на двух уровнях:

• уровень обязательной подготовки (УОП), который должны достичь все учащиеся;

• уровень, характеризующий результаты, к которым могут стремиться и которых при желании могут достичь школьники, изучающие общеобразовательный курс, т.е. уровень возможностей (УВ)

Алгебра и начала анализа

Числовые функции

УОП: Знать понятие функции и другие функциональные терминологии; понятия о возрастании и убывании функции, промежутках знакопостоянства; основные функции курса алгебры 7 – 9 классов и их свойства; понятия четной и нечетной функции.

УВ: правильно употреблять функциональную терминологию, понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком и решать; решать обратную задачу; находить по графику промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения

Тригонометрические функции

УОП: знать определение числового и углового аргумента; радианную меру угла; основные формулы, выражающие зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же аргумента; основное тригонометрическое тождество; знать и уметь применять формулы приведения, таблицу значений тригонометрических функций и справочный материал. Изображать графики основных тригонометрических функций и описывать свойства этих функций; определять значение функции по значению аргумента; знать основные преобразования графиков функций и .

УВ: знать формулы половинного аргумента; уметь строить графики сложных функций с помощью последовательных преобразований графиков элементарных функций и использовать их для описания реальных зависимостей.

Тригонометрические уравнения

УОП: знать определение арккосинуса, арксинуса, арктангенса, арккотангенса числа; выполнять вычислительные примеры с помощью таблицы значений тригонометрических функций; знать формулы для нахождения корней уравнений ,, и уметь решать простейшие тригонометрические уравнения; знать основные приемы решения тригонометрических уравнений.

УВ: уметь вычислять arcsin(sin α), tg(arcsin a), cos(arcsin a), sin(arccosa), arccos(tg α); владеть приемами решения тригонометрических уравнений (разложение на множители, подстановки; замены переменной, методом решения однородных тригонометрических уравнений); решать простейшие тригонометрические неравенства.

Преобразование тригонометрических выражений

УОП: знать формулы синуса, косинуса и тангенса суммы и разности двух углов; формулы синуса, косинуса двойного угла. Уметь выполнять несложные преобразования тригонометрических выражений. Использовать приобретенные знания для практических расчетов по формулам с применением справочных материалов и простейших вычислительных устройств.

УВ: знать формулы понижения степени, выполнять преобразования суммы тригонометрических функций в произведение и произведение в сумму; владеть развитой техникой выполнения тождественных преобразований тригонометрических выражений (упрощение выражений, доказательство тождеств, сокращение дробей при решении уравнений)

Производная

УОП: понимать смысл понятий: последовательность, числовой ряд, предел последовательности, предел функции; уметь находить значение членов последовательности и вычислять предел последовательности; понимать и физический геометрический смысл производной; находить производные элементарных функций, пользуясь таблицей производных и правилами дифференцирования; составлять уравнение касательной, пользуясь алгоритмом.

УВ: уметь вычислять производные, применяя правила вычисления производных; знать физический и геометрический смысл производной; знать алгоритмом составления уравнения касательной к графику функции у = f (x); решать задачи с применением уравнения касательной к графику функции; приобрести навыки вычисления пределов, суммы бесконечной геометрической прогрессии; уметь строить эскизы графиков.

Применение производной к построению графиков функций

УОП: уметь применять производные для исследования функции на монотонность в несложных случаях и при исследовании функции на экстремумы; находить наибольшее и наименьшее значения функции на отрезке.

УВ: уметь применять дифференциальное исчисление для исследования элементарных функций и построения графиков; использовать производные при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольшего и наименьшего значений.

Геометрия

Введение. Аксиомы стереометрии и их следствия.

УОП: уметь распознавать на чертежах и моделях указанные объекты; знать правила изображения пространственных фигур на плоскости; уметь пользоваться геометрическими инструментами (линейка, угольник, циркуль, транспортир).

УВ: знать основные понятия и аксиомы стереометрии и их связь с аксиомами планиметрии.

Параллельность прямых и плоскостей

УОП: знать определения: параллельных прямых и их свойство; скрещивающихся прямых; прямой, параллельной плоскости; параллельных плоскостей. Знать форму­лировки: признака параллельности прямой и плоскости; признака параллельности двух плоскостей; свойства параллельных плоскостей. Уметь формулировать опреде­ление: угла с сонаправленными сторонами; угла между скрещивающимися пря­мыми.

УВ: видеть общность и различие свойств аналогичных структур на плоскости и в пространстве; уметь решать задачи на доказательство и строить сечения тетраэдра и параллелепипеда, проводя логические рассуждения.

Перпендикулярность прямых и плоскостей.

УОП: знать определения: перпендикулярных прямых в пространстве; прямой, пер­пендикулярной к плоскости; перпендикулярных плоскостей. Уметь формулировать признак перпендикулярности прямой и плоскости; перпендикулярности двух плос­костей. Уметь определять в пространстве: угол между прямой и плоскостью; дву­гранный угол и его линейный угол; строить на чертеже линейный угол двугранного угла. Уметь находить расстояние: от точки до плоскости; между прямой и парал­лельной плоскостью; между параллельными плоскостями, проводя аргументацию в ходе решения задач; знать понятие перпендикуляра и наклонной к плоскости в про­странстве; уметь строить проекцию наклонной на плоскость.

УВ: видеть общность и различие свойств аналогичных структур на плоскости и в пространстве; уметь решать стереометрические задачи на основе систематизации знаний о перпендикулярности и параллельности прямых и плоскостей в простран­стве.

Многогранники.

УОП: уметь решать задачи: требующие распознавания различных видов многогран­ников (призм, пирамид) и форм их сечения; на вычисление элементов треугольной призмы и пирамиды с применением аппарата алгебры и тригонометрии; на вычис­ление элементов четырех угольных призм и пирамид; изображать соответствующий многогранник на чертеже; знать и уметь применять формулы для нахождения пло­щадей боковой и полной поверхности призмы и правильной пирамиды.

УВ: уметь решать задачи на вычисление элементов треугольной призмы и пирамиды с применением аппарата алгебры и тригонометрии; задачи, связанные с использова­нием изученных формул вычисления элементов правильных многоугольников; иметь представление о различных видах правильных многогранников; уметь приме­нять теоретический материал темы при вычислении элементов многогранников.

Векторы

УОП: уметь обобщать изученный в основной школе материал о векторах на плоско­сти, проводя аналогию при систематизации сведений о действиях с векторами в пространстве; уметь решать задачи векторным методом.

УВ: владеть понятием компланарных векторов и разложением вектора по трем не­компланарным векторам.

1. КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН

Алгебра и начала анализа

№ урока	Содержание учебного материала	часы	дата			примечание
			план	факт
	Глава 1. Числовые функции	5
1	Определение числовой функции и способы ее задания.	1
2	Определение числовой функции и способы ее задания.	1
3	Свойства функций.	1
4	Свойства функций.	1
5	Обратная функция.	1
	Глава 2. Тригонометрические функции	26
6	Числовая окружность.	1
7	Числовая окружность	1
8	Числовая окружность на координатной плоскости.	1
9	Числовая окружность на координатной плоскости	1
10	Повторительно-обобщающий урок по теме «Числовые функции».	1
11	Контрольная работа №1 по теме «Числовые функции».	1
12	Синус и косинус. Тангенс и котангенс.	1
13	Синус и косинус. Тангенс и котангенс.	1
14	Синус и косинус. Тангенс и котангенс.	1
15	Тригонометрические функции числового аргумента.	1
16	Тригонометрические функции числового аргумента.	1
17	Тригонометрические функции углового аргумента.	1
18	Формулы приведения.	1
19	Формулы приведения.	1
20	Повторительно-обобщающий урок по теме «Определение тригонометрических функций»	1
21	Контрольная работа №2 по теме «Определение тригонометрических функций»	1
22	Функция у = sin х, ее свойства и график.	1
23	Функция у = sin х, ее свойства и график.	1
24	Функция у = cos x, ее свойства и график.	1
25	Функция у = cos x, ее свойства и график.	1
26	Периодичность функций y = sin x, y = cos x.	1
27	Преобразование графиков тригонометрических функций.	1
28	Преобразование графиков тригонометрических функций.	1
29	Функции y = tg x, y = ctg x, их свойства и график.	1
30	Повторительно-обобщающий урок по теме «Свойства и графики тригонометрических функций».	1
31	Контрольная работа №3 по теме «Свойства и графики тригонометрических функций»	1
	Глава 3. Тригонометрические уравнения	11
32	Арккосинус. Решение уравнения cos t = а.	1
33	Арккосинус. Решение уравнения cos t = а.	1
34	Арксинус. Решение уравнения sin t =a.	1
35	Арксинус. Решение уравнения sin t =a.	1
36	Арктангенс и арккотангенс. Решение уравнений tg t = a, ctg t =a.	1
37	Тригонометрические уравнения.	1
38	Тригонометрические уравнения	1
39	Тригонометрические уравнения	1
40	Тригонометрические уравнения	1
41	Повторительно-обобщающий урок по теме «Тригонометрические уравнения	1
42	Контрольная работа №4 по теме «Тригонометрические уравнения».	1
	Глава 4. Преобразование тригонометрических выражений.	15
43	Синус и косинус суммы и разности аргументов.	1
44	Синус и косинус суммы и разности аргументов.	1
45	Синус и косинус суммы и разности аргументов.	1
46	Тангенс суммы и разности аргументов.	1
47	Тангенс суммы и разности аргументов.	1
48	Формулы двойного аргумента.	1
49	Формулы двойного аргумента.	1
50	Формулы двойного аргумента.	1
51	Преобразование сумм тригонометрических функций в произведение.	1
52	Преобразование сумм тригонометрических функций в произведение.	1
53	Преобразование сумм тригонометрических функций в произведение.	1
54	Преобразование произведений тригонометрических функций в суммы.	1
55	Преобразование произведений тригонометрических функций в суммы.	1
56	Повторительно-обобщающий урок по теме «Преобразование тригонометрических выражений».	1
57	Контрольная работа №5 по теме «Преобразование тригонометрических выражений».	1
58	Глава 5. Производная	34
59	Числовые последовательности и их свойства. Предел последовательности.	1
60	Сумма бесконечной геометрической прогрессии.	1
61	Предел функции.	1
62	Предел функции.	1
63	Предел функции.	1
64	Определение производной.	1
65	Определение производной.	1
66	Определение производной.	1
67	Вычисление производных.	1
68	Вычисление производных.	1
69	Вычисление производных.	1
70	Вычисление производных.	1
71	Повторительно-обобщающий урок по теме «Вычисление производных».	1
72	Контрольная работа №6 по теме «Вычисление производных».	1
73	Уравнение касательной к графику функции.	1
74	Уравнение касательной к графику функции.	1
75	Применение производной для исследований функций на монотонность и экстремумы.	1
76	Применение производной для исследований функций на монотонность и экстремумы.	1
77	Применение производной для исследований функций на монотонность и экстремумы.	1
78	Построение графиков функций.	1
79	Построение графиков функций	1
80	Построение графиков функций	1
81	Подготовка к контрольной работе по теме «Применение производной к исследованию функций».	1
82	Контрольная работа №7 по теме «Применение производной к исследованию функций».	1
83	Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке.	4
84	Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке.
85	Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке.
86	Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке.
87	Задачи на отыскание наибольших и наименьших значений величин.	4
88	Задачи на отыскание наибольших и наименьших значений величин.
89	Задачи на отыскание наибольших и наименьших значений величин.
90	Задачи на отыскание наибольших и наименьших значений величин.
91	Контрольная работа №8 по теме «Применение производной»	2
	Повторение.	11
92	Тригонометрические функции.	2
93	Тригонометрические функции.
94	Тригонометрические уравнения.	2
95	Тригонометрические уравнения.
96	Преобразование тригонометрических выражений.	2
97	Преобразование тригонометрических выражений
98	Производная.	2
99	Производная.
100-101	Итоговая контрольная работа.	2
	Резерв	1
	Итого	102

Геометрия

№ урока	Содержание учебного материала	часы	дата		примечание
			план	факт
	Введение ( аксиомы стереометрии и их свойства).	5
1	п.п.1,2.Предмет стереометрии. Аксиомы стереометрии.	1
2	п.3.Некоторые следствия из аксиом.	1
3	Решение задач на применение аксиом и следствий.	1
4	Решение задач на применение аксиом и следствий.	1
5	Решение задач на применение аксиом и следствий.	1
	Глава 1. Параллельность прямых и плоскостей.	19
6	п.п.4,5. Параллельные прямые в пространстве. Параллельность трех прямых.	1
7	п.6. Параллельность прямой и плоскости.	1
8	Решение задач по теме «Параллельность прямой и плоскости»	1
9	Решение задач по теме «Параллельность прямой и плоскости	1
10	п.7.Скрещивающиеся прямые.	1
11	п.п.8,9. Углы с сонаправленными сторонами. Угол между прямыми.	1
12	Решение задач по теме «Взаимное расположение прямых в пространстве»	1
13	Решение задач по теме «Угол между двумя прямыми»	1
14	Решение задач по теме «Параллельность прямых и плоскостей»	1
15	Контрольная работа №1 по теме «Параллельность прямых и плоскостей»	1
16	п.10. Параллельные плоскости. Признак параллельности двух плоскостей.	1
17	п.11. Свойства параллельных плоскостей.	1
18	п.п.12,13. Тетраэдр	1
19	п.п.12,13.Параллелепипед.	1
20	Задачи на построение сечений.	1
21	Задачи на построение сечений.	1
22	Решение задач по теме «Параллельность плоскостей. Тетраэдр и параллелепипед»	1
23	Решение задач по теме «Параллельность плоскостей. Тетраэдр и параллелепипед»	1
24	Контрольная работа №2 по теме «Параллельность плоскостей. Тетраэдр и параллелепипед»	1
	Глава 2. Перпендикулярность прямых и плоскостей.	20
25	п.п. 15,16. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.	1
26	п.17. Признак перпендикулярности прямой и плоскости.	1
27	п.18. Теорема о прямой, перпендикулярной к плоскости.	1
28	Решение задач на перпендикулярность прямой и плоскости.	1
29	Решение задач на перпендикулярность прямой и плоскости.	1
30	Решение задач на перпендикулярность прямой и плоскости.	1
31	п.п.19,20.Расстояние от точки до плоскости. Теорема о трех перпендикулярах.	1
32	п.20Угол между прямой и плоскостью.	1
33	Решение задач на применение теоремы о трех перпендикулярах.	1
34	Решение задач на применение теоремы о трех перпендикулярах.	1
35	Решение задач на угол между прямой и плоскостью	1
36	Решение задач на угол между прямой и плоскостью	1
37	п.22.Двугранный угол.	1
38	п.23.Признак перпендикулярности двух плоскостей.	1
39	п.24. Прямоугольный параллелепипед.	1
40	Решение задач на свойства прямоугольного параллелепипеда	1
41	Решение задач по теме «Перпендикулярность прямых и плоскостей».	1
42	Решение задач по теме «Перпендикулярность прямых и плоскостей».	1
43	Решение задач по теме «Перпендикулярность прямых и плоскостей».	1
44	Контрольная работа №3 по теме «Перпендикулярность прямых и плоскостей».	1
	Глава 3. Многогранники.	12
45	п.27. Понятие многогранника.	1
46	п.30. Призма. Площадь поверхности призмы.	1
47	Решение задач на вычисление площади поверхности призмы	1
48	Решение задач на вычисление площади поверхности призмы	1
49	п.32.Пирамида.	1
50	п.33. Правильная пирамида.	1
51	Решение задач по теме «Пирамида».	1
52	п.34.Усеченная пирамида. Площадь поверхности пирамиды.	1
53	Решение задач по теме «Усеченная пирамида. Площадь поверхности пирамиды.»	1
54	п.п. 35,36. Симметрия в пространстве. Понятие правильного многогранника.	1
55	п.37. Элементы симметрии правильных многогранников.	1
56	Контрольная работа №4 по теме «Многогранники».	1
	Глава 4. Векторы в пространстве	6
57	п.п. 38,39. Понятие вектора в пространстве. Равенство векторов.	1
58	п.п.40,41.Сложение и вычитание векторов. Сумма нескольких векторов.	1
59	п.42.Умножение вектора на число.	1
60	п.п.43,44. Компланарные векторы. Правило параллелепипеда.	1
61	п.45. Разложение вектора по трем некомпланарным векторам.	1
62	Решение задач по теме «Векторы в пространстве».	1
	Итоговое повторение курса геометрии 10-го класс.	6
63	Параллельность прямых и плоскостей.	1
64	Перпендикулярность прямых и плоскостей.	1
65	Перпендикулярность прямых и плоскостей.	1
66	Многогранники.	1
67	Многогранники.	1
	Резерв	1
	итого	68

1. КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ И ДИДАКТИЧЕСКИЕМАТЕРИАЛЫ

Алгебра и начала анализа

Контрольная работа № 1

Вариант 1

1. Задает ли указанное правило функцию

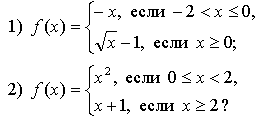
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 1, 3, –1;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки 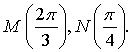Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция убывает на R. Решите неравенство

Вариант 2

1. Задает ли указанное правило функцию

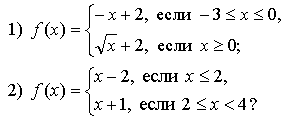
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках –4, –2, 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки 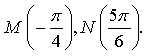Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция возрастает на R. Решите неравенство

Контрольная работа № 2

Вариант 1

1. Вычислите.

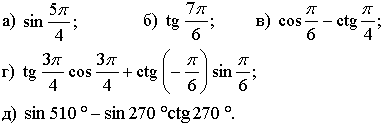
2. Упростите выражение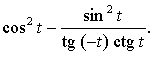

3. Решите уравнение.

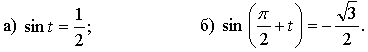
4. Известно, что Найдите:

5. Расположите в порядке возрастания следующие числа:

Вариант 2

1. Вычислите.

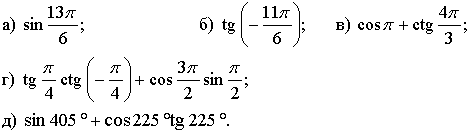
2. Упростите выражение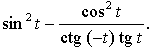

3. Решите уравнение.

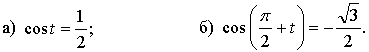
4. Известно, что 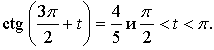Найдите:

5. Расположите в порядке убывания следующие числа:

Контрольная работа № 3

Вариант 1

1. Не выполняя построения, установите, принадлежит ли графику функции 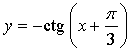точка:

2. Исследуйте функцию на четность.

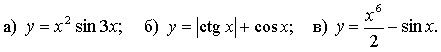
3. Исследуйте функцию на периодичность; укажите основной период, если он существует.

4. Решите графически уравнение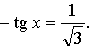

5. Постройте графики функций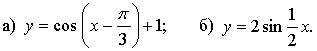

Вариант 2

1. Не выполняя построения, установите, принадлежит ли графику функции 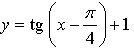точка:

2. Исследуйте функцию на четность.

3. Исследуйте функцию на периодичность; укажите основной период, если он существует.

4. Решите графически уравнение

5. Постройте графики функций

Контрольная работа № 4

Вариант 1

Решите уравнения:

1.

2.

3.

4.

5. Решите уравнение:

6. Найдите корни уравнения принадлежащие отрезку

Вариант 2

Решите уравнения:

1.

2.

3.

4.

5. Решите уравнение:

6. Найдите корни уравнения принадлежащие отрезку

Контрольная работа № 5

Вариант 1

1. Вычислите.

а)

б)

в)

2. Упростите выражение

3. Решите уравнение

4. Найдите корни уравнения принадлежащие полуинтервалу

5. Решите уравнение

6. Докажите, что для любого х справедливо неравенство

Вариант 2

1. Вычислите.

а)

б)

в)

2. Упростите выражение

3. Решите уравнение

4. Найдите корни уравнения принадлежащие промежутку

5. Решите уравнение

6. Докажите, что для любого х справедливо неравенство

Контрольная работа № 6

Вариант 1

1. Вычислите 1, 5 и 100-й члены последовательности, если ее п-й член задается формулой

2. Представьте бесконечную периодическую десятичную дробь 1,(18) в виде обыкновенной дроби.

3. Найдите производную функции.

а) б)

в) г)

4. Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

5. Докажите, что функция удовлетворяет соотношению

6. Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой каждый член в 6 раз больше суммы всех её последующих членов.

Вариант 2

1. Вычислите 1, 7 и 200-й члены последовательности, если ее п-й член задается формулой

2. Представьте бесконечную периодическую десятичную дробь 2,(27) в виде обыкновенной дроби.

3. Найдите производную функции.

а) б)

в) г)

4. Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

5. Докажите, что функция удовлетворяет соотношению

6. Сумма бесконечной убывающей геометрической прогрессии равна 4, а сумма квадратов её членов равна 48. Найдите первый член и знаменатель прогрессии.

Контрольная работа № 7

Вариант 1

1. Составьте уравнение касательной к графику функции в точке

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точку ппересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна биссектрисе первой координатной четверти.

Вариант 2

1. Составьте уравнение касательной к графику функции в точке

2. Составьте уравнения касательных к графику функции в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.

3. Исследуйте функцию на монотонность и экстремумы и постройте её график.

4. Найдите значение параметра а, при котором касательная к графику функции в точке с абсциссой параллельна прямой

Контрольная работа № 8

Вариант 1

1. Найдите наименьшее и наибольшее значения функции.

а) на отрезке [0; 1];

б) на отрезке [–; 0].

2. Найдите диагональ прямоугольника наибольшей площади, вписанного в прямоугольный треугольник с катетами 18 см и 24 см и имеющего с ним общий прямой угол.

3. Исследуйте функцию на монотонность и экстремумы.

4. При каких значениях параметра а уравнение имеет три корня?

Вариант 2

1. Найдите наименьшее и наибольшее значения функции.

а) на отрезке [–2; 1];

б) на отрезке

2. В прямоугольном треугольнике с катетами 36 и 48 на гипотенузе взята точка. Из неё проведены прямые, параллельные катетам. Получился прямоугольник, вписанный в данный треугольник. Где на гипотенузе надо взять точку, чтобы площадь такого прямоугольника была наибольшей?

3. Исследуйте функцию на монотонность и экстремумы.

4. При каких значениях параметра а уравнение имеет два корня?

Геометрия

Контрольная работа № 1

Вариант I

1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.

а) Каково взаимное положение прямых ЕF и АВ?

б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните.

2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.

а) Выполните рисунок к задаче.

б) Докажите, что полученный четырехугольник есть ромб.

Вариант II

1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.

а) Каково взаимное положение прямых РK и АВ?

б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните.

2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

а) Выполните рисунок к задаче.

б) Докажите, что четырехугольник MNEK есть трапеция.

Контрольная работа № 2

Вариант I

1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:

а) параллельными;

б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₂В₂, если А₁В₁ = 12 см, В₁О : ОВ₂ = 3 : 4.

3. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD₁.

Вариант II

1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:

а) параллельными;

б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₁В₁, если А₂В₂ = 15 см, ОВ₁ : ОВ₂ = 3 : 5.

3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.

Контрольная работа № 3

Вариант I

1. Диагональ куба равна 6 см. Найдите:

а) ребро куба;

б) косинус угла между диагональю куба и плоскостью одной из его граней.

2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла DABM,
М α.

в) Найдите синус угла между плоскостью ромба и плоскостью α.

Вариант II

1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла BADM,
М α.

в) Найдите синус угла между плоскостью квадрата и плоскостью α.

Контрольная работа № 4

Вариант I

1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD₁C₁ составляет с плоскостью основания угол в 60°. Найдите:

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

Вариант II

1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а) меньшую высоту параллелограмма;

б) угол между плоскостью АВС₁ и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

1. ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

1.Мордкович А.Г. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. М., «Мнемозина», 2009.

2.Мордкович А.Г., Мишустина Т.Н. Тульчинская Е.Е. Алгебра и начала анализа. 10 - 11 классы. Задачник для общеобразовательных учреждений. М., «Мнемозина», 2006.

3.А.Г. Мордкович Алгебра и начала анализа.10-11.Методическое пособие для учителя. – М.: Мнемозина, 2009.

4. Контрольные работы по алгебре и началам анализа для 10 – 11 классов, базовое обучение. / А.Г. Мордкович, Е.Е. Тульчинская. / М: Мнемозина, 2010.

5.Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119.

6.В. И. Глизбург Алгебра и начала анализа 10 класс. Контрольные работы. Базовый уровень - М.: Мнемозина 2009 г.;

7.Л. А. Александрова. Алгебра и начала анализа. Самостоятельные работы- М.: Мнемозина 2009 г.

8.Математика: Сборник заданий для подготовки проведения письменного экзамена курсу средней школы. 11кл, М.: Дрофа, 2000

9.Ершова А.П. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2002.

10. Контрольно-измерительные материалы. Алгебра и начала анализа: 10 класс/сос. А.Н. Рурукин.- М.: ВАКО, 2012.

11.Атанасян Л.С. и др. Геометрия. Учебник для 10-11 кл. М., Просвещение, 2009.

12.Поурочные разработки по геометрии: 10 класс/Сост. В.А. Яровенко.- М.: ВАКО,2009

13.Зив Б.Г. Дидактические материалы по геометрии для 10-11 кл. М., Просвещение, 2008

Интернет-ресурсы:

• Министерство образования РФ

1. http://www.informika.ru/

2. http://www.ed.gov.ru/

3. http://www.edu.ru/

• Тестирование online: 5 - 11 классы

1. http://www.kokch.kts.ru/cdo/

2. http://uztest.ru/

• Педагогическая мастерская, уроки в Интернет и многое другое

1. http://teacher.fio.ru

2. http://www.it-n.ru/

3. http://pedsovet.org/

4. http://www.uchportal.ru/

• Новые технологии в образовании

1. http://www.sumirea.ru/narticle702.html

2. http://www.int-edu.ru/

• Мегаэнциклопедия Кирилла и Мефодия

1. http://mega.km.ru

• сайты «Мир энциклопедий», например:

1. http://www.encyclopedia.ru/