Муниципальное бюджетное образовательное учреждение
г. Астрахань «Средняя общеобразовательная школа № 13»
Утверждаю Согласовано Рассмотрено на заседании
Директор Зам. директора по УВР МО учителей
МБОУ СОШ № 13 политехнического цикла
Протокол № _____
____ Л.В. Рахманова _______ И.А.Савчук от «_____» _________2016г.
«____» _________2016г. «_______»_______2016г. ________ Н.В. Бурмакина
Рабочая программа
по геометрии
для 10 класса
на 2016- 2017 учебный год
Разработчик программы
Учитель математики
Бурмакина Нина Владимировна
Высшая квалификационная категория
2016 год
Пояснительная записка.
Рабочая программа составлена на основе федерального компонента государственного стандарта среднего (полного)общего образования, примерной программы по математике основного общего образования, авторской программы «Геометрия, 10 – 11», авт. Л.С. Ананаса и др., федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2015-16 учебный год, с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования.
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательная линия: «Геометрия». В рамках указанной содержательной линии решаются следующие задачи:
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач.
Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Обще учебные умения, навыки и способы деятельности
В ходе освоения содержания геометрического образования, учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ десятиклассников по геометрии
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности.
уметь
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание курса
к учебнику Л.С. Атанасяна и др. «Геометрия, 10-11»,
10 класс (базовый уровень 2 ч в неделю, всего 68 часов).
Введение (5 час).
Предмет стереометрии. Основные понятия стереометрии (точка, прямая, плоскость, пространство) и аксиомы стереометрии. Первые следствия из аксиом.
Параллельность прямых и плоскостей (19 часов, из них 2 часа контрольные работы, 1 час зачет).
Пересекающиеся, параллельные и скрещивающиеся прямые. Параллельность прямой и плоскости, признак и свойства. Угол между прямыми в пространстве. Перпендикулярность прямых.
1Параллельность плоскостей, признаки и свойства. Параллельное проектирование. И1зображение пространственных фигур.
Тетраэдр и параллелепипед, куб. Сечения куба, призмы, пирамиды.
Перпендикулярность прямых и плоскостей (21 час, из них 1 час контрольная работа, 1 час зачет).
Перпендикулярность прямой и плоскости, признаки и свойства. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Площадь ортогональной проекции многоугольника.
Многогранники (12 часов, из них 1 час контрольная работа, 1 час зачет).
Понятие многогранника, вершины, ребра, грани многогранника. Развертка. Многогранные углы Выпуклые многогранники. Теорема Эйлера.
Призма, ее основание, боковые ребра, высота, боковая и полная поверхности.
Прямая и наклонная призма. Правильная призма.
Пирамида, ее основание, боковые ребра, высота, боковая и полная поверхности. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрия в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая и зеркальная). Примеры симметрий в окружающем мире.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Векторы в пространстве (6 часов, из них 1 час зачет).
Понятие вектора в пространстве. Модуль вектора. Равенство векторов. Сложение и вычитание векторов. Коллинеарные векторы. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным векторам.
Повторение курса геометрии 10 класса (6 часов)
Календарно- тематическое планирование
по геометрии 10 класса
2 часа в неделю, всего- 68 часов
| № урока | Содержание (тема урока) | Кол-во часов | Дата проведения | Контроль | Используемые ресурсы | Примечание | ||||||
| план | факт | |||||||||||
| Введение | 3 |
|
|
|
|
| ||||||
| 1 | Предмет стереометрии. Основные понятия и аксиомы стереометрии | 1 |
|
|
|
|
| |||||
| 2 | Предмет стереометрии. Основные понятия и аксиомы стереометрии | 1 |
|
| C/р | карточки |
| |||||
| 3 | Первые следствия из теорем | 1 |
|
|
|
|
| |||||
| Глава 1 Параллельность прямых и плоскостей | 16 |
|
|
|
|
| ||||||
| 4 | Параллельность прямых, прямой и плоскости | 1 |
|
| диктант | тест |
| |||||
| 5 | Параллельность прямых, прямой и плоскости | 1 |
|
|
|
|
| |||||
| 6 | Параллельность прямых, прямой и плоскости | 1 |
|
|
|
|
| |||||
| 7 | Параллельность прямых, прямой и плоскости | 1 |
|
| с/р | карточки |
| |||||
| 8 | Взаимное расположение прямых в пространстве | 1 |
|
|
|
|
| |||||
| 9 | Угол между прямыми | 1 |
|
| диктант | тест |
| |||||
| 10 | Угол между прямыми | 1 |
|
|
|
|
| |||||
| 11 | Контрольная работа № 1 | 1 |
|
| к/р | карточки |
| |||||
| 12 | Параллельность плоскостей | 1 |
|
|
|
|
| |||||
| 13 | Параллельность плоскостей | 1 |
|
| диктант | тест |
| |||||
| 14 | Тетраэдр и параллелепипед | 1 |
|
| с/р | карточки |
| |||||
| 15 | Тетраэдр и параллелепипед | 1 |
|
|
|
|
| |||||
| 16 | Тетраэдр и параллелепипед | 1 |
|
| диктант | тест |
| |||||
| 17 | Тетраэдр и параллелепипед | 1 |
|
| с/р | карточки |
| |||||
| 18 | Контрольная работа № 2 | 1 |
|
| к/р | карточки |
| |||||
| 19 | Решение задач | 1 |
|
| с/р | карточки |
| |||||
| Глава 2 Перпендикулярность прямых и плоскостей | 17 |
|
|
|
|
| ||||||
| 20 | Перпендикулярность прямой и плоскости | 1 |
|
| диктант | тест |
| |||||
| 21 | Перпендикулярность прямой и плоскости | 1 |
|
|
|
|
| |||||
| 22 | Перпендикулярность прямой и плоскости | 1 |
|
|
|
|
| |||||
| 23 | Перпендикулярность прямой и плоскости | 1 |
|
|
|
|
| |||||
| 24 | Перпендикулярность прямой и плоскости | 1 |
|
| с/р | карточки |
| |||||
| 25 | Перпендикуляр и наклонные | 1 |
|
| диктант | тест |
| |||||
| 26 | Перпендикуляр и наклонные | 1 |
|
|
|
|
| |||||
| 27 | Перпендикуляр и наклонные | 1 |
|
| с/р | карточки |
| |||||
| 28 | Угол между прямой и плоскостью | 1 |
|
|
|
|
| |||||
| 29 | Угол между прямой и плоскостью | 1 |
|
| диктант | тест |
| |||||
| 30 | Угол между прямой и плоскостью | 1 |
|
| с/р | карточки |
| |||||
| 31 | Двугранный угол | 1 |
|
| диктант | тест |
| |||||
| 32 | Двугранный угол | 1 |
|
| с/р | карточки |
| |||||
| 33 | Перпендикулярность плоскостей | 1 |
|
| диктант | тест |
| |||||
| 34 | Перпендикулярность плоскостей | 1 |
|
| с/р | карточки |
| |||||
| 35 | Контрольная работа № 3 | 1 |
|
| к/р | карточки |
| |||||
| 36 | Решение задач | 1 |
|
|
|
|
| |||||
| Глава 3 Многогранники | 14 |
|
|
|
|
| ||||||
| 37 | Понятие многогранника | 1 |
|
|
|
|
| |||||
| 38 | Призма | 1 |
|
| диктант | тест |
| |||||
| 39 | Призма | 1 |
|
| с/р | карточки |
| |||||
| 40 | Пирамида | 1 |
|
| диктант | тест |
| |||||
| 41 | Пирамида | 1 |
|
| с/р | карточки |
| |||||
| 42 | Пирамида | 1 |
|
|
|
|
| |||||
| 43 | Пирамида | 1 |
|
|
|
|
| |||||
| 44 | Правильные многогранники | 1 |
|
| диктант | тест |
| |||||
| 45 | Правильные многогранники | 1 |
|
|
|
|
| |||||
| 46 | Правильные многогранники | 1 |
|
| с/р | карточки |
| |||||
| 47 | Правильные многогранники | 1 |
|
| диктант | тест |
| |||||
| 48 | Правильные многогранники | 1 |
|
|
|
|
| |||||
| 49 | Контрольная работа № 4 | 1 |
|
| к/р | карточки |
| |||||
| 50 | Решение задач | 1 |
|
|
|
|
| |||||
| Заключительное повторение | 20 |
|
|
|
|
| ||||||
| 51 | Многогранники | 1 |
|
| диктант | тест |
| |||||
| 52 | Многогранники | 1 |
|
|
|
|
| |||||
| 53 | Многогранники | 1 |
|
|
|
|
| |||||
| 54 | Многогранники | 1 |
|
|
|
|
| |||||
| 55 | Многогранники | 1 |
|
|
|
|
| |||||
| 56 | Многогранники | 1 |
|
| с/р | карточки |
| |||||
| 57 | Параллельность плоскостей | 1 |
|
|
|
|
| |||||
| 58 | Параллельность плоскостей | 1 |
|
| диктант | тест |
| |||||
| 59 | Параллельность плоскостей | 1 |
|
|
|
|
| |||||
| 60 | Параллельность плоскостей | 1 |
|
| с/р | карточки |
| |||||
| 61 | Параллельность плоскостей | 1 |
|
|
|
|
| |||||
| 62 | Параллельность плоскостей | 1 |
|
|
|
|
| |||||
| 63 | Перпендикулярность плоскостей | 1 |
|
| с/р | карточки |
| |||||
| 64 | Перпендикулярность плоскостей | 1 |
|
| диктант | тест |
| |||||
| 65 | Перпендикулярность плоскостей | 1 |
|
|
|
|
| |||||
| 66 | Перпендикулярность плоскостей | 1 |
|
| с/р | карточки |
| |||||
| 67 | Перпендикулярность плоскостей | 1 |
|
| диктант | тест |
| |||||
| 68 | Заключительный урок | 1 |
|
| с/р | карточки |
| |||||
КОНТРОЛЬНЫЕ РАБОТЫ 10 КЛАССА
Контрольная работа №1
по теме «Аксиомы стереометрии. Параллельность прямой и плоскости»
Вариант 1
Каково взаимное расположение прямой b и точки А, если известно, что через них можно провести: а) единственную плоскость; б) несколько плоскостей? Ответ обоснуйте. Выполните соответствующие чертежи.
Треугольники ADC и BDC расположены так, что точка А не лежит в плоскости BCD. Точка М - середина отрезка AD, о — точка пересечения медиан треугольника BCD. Определите положение точки пересечения прямой МО с плоскостью ABC.
Параллелограмм ABCD и треугольник DAM расположены так, что точка М не принадлежит плоскости ABC. Точка о — точка пересечения диагоналей ABCD. Найдите линию пересечения плоскостей: а) ВМС и OMD; б) BMD и АСМ.
Точка М не лежит ни на одной из двух скрещивающихся прямых. Докажите, что через эту точку проходит плоскость, параллельная каждой из этих прямых, и притом только одна.
Вариант 2
Каково взаимное расположение прямых, а и b, если известно, что через них можно провести: а) единственную плоскость; б) несколько плоскостей? Ответ обоснуйте. Выполните соответствующие чертежи.
Треугольники ABC и ABD расположены так, что точка С не лежит в плоскости ABD. Точка Н — середина отрезка AD.O- точка пересечения медиан треугольника А ВС. Определите положение точки пересечения прямой, НО с плоскостью DBC.
Параллелограмм ABCD и треугольник ВСК расположены так, что точка K не принадлежит плоскости ABC. Точка о — точка пересечения диагоналей ABCD. Найдите линию пересечения плоскостей: a) ADK и ОСК; б) BDK и АС К.
Прямая, а и параллельная ей плоскость не проходят через точку М. Докажите, что через точку М проходит прямая, параллельная прямой, а и плоскости, и притом только одна.
Контрольная работа № 2
по теме «Параллельность прямых и плоскостей»
Вариант 1
Точки А, В, С и D не лежат в одной плоскости, а точки Р и М лежат на отрезках AD и АВ соответственно так, что АР = 3 PD и AM = MB
Постройте точку пересечения прямой РМ с прямой BD
Докажите, что прямые РМ и CD не пересекаются.
Постройте плоскость, проходящую через точки Р и М параллельно прямой АС, и определите, в каком отношении эта плоскость делит ребро CD
Постройте плоскость, проходящую через точку P параллельно плоскости BCD, и определите, в каком отношении эта плоскость делит площадь треугольника АВС.
Точка Р лежит на ребре АВ параллелепипеда ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точку Р и параллельной плоскости А1D1С.
Вариант 2
Точки А, В, С и D не лежат в одной плоскости, а точки Н и М лежат на отрезках CD и ВС соответственно так, что МС = 2 ВМ и DH = НС
Постройте точку пересечения прямой HМ с прямой BD
Докажите, что прямые НМ и АС не пересекаются
Постройте плоскость, проходящую через точки H и М параллельно прямой АС, и определите, в каком отношении эта плоскость делит отрезок АВ.
Постройте плоскость, проходящую через точку М параллельно плоскости ABD, и определите, в каком отношении эта плоскость делит площадь треугольника A DC.
Точка М лежит на ребре AA1, параллелепипеда ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точку М и параллельной плоскости B1C1D.
Контрольная работа № 3
по теме «Перпендикулярность прямых и плоскостей»
Вариант 1
Через вершину к треугольнику DKP проведена прямая КМ, перпендикулярная плоскости этого треугольника. Известно, что КМ= 15 см, DP = 12 см, DK = РК = 10 см. Найдите расстояние от точки М до прямой DP.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол B1ADB, если известно, что четырехугольник ABCD — квадрат, АС= 6
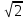 см, AB1 =4
см, AB1 =4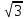 см.
см.Дан прямоугольный параллелепипед, угол между прямыми А1С и BD прямой. Определите вид четырехугольника ABCD.
Вариант 2
Через вершину к треугольнику КМР проведена прямая КЕ, перпендикулярная плоскости этого треугольника. Известно, что КЕ = 8 см, MP = = 2
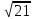 см. МК= РК. Найдите КМ, если расстояние от точки Е до прямой MP равно 2
см. МК= РК. Найдите КМ, если расстояние от точки Е до прямой MP равно 2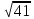 см.
см.Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол C1ADB, если BD= 6
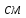 , AD = 6 см, АА1 = 2
, AD = 6 см, АА1 = 2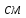
Дан прямоугольный параллелепипед ABCDA1B1C1D1.угол между прямыми В1С и DC1, равен 60°. Определите вид четырехугольника ВВ1С1С.
Контрольная работа № 4
по теме «Многогранники»
Вариант 1
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 4 и 8 см, угол BAD равен 60". Диагональ В1D образует с плоскостью основания угол, равный 30°. Найдите площадь боковой поверхности призмы.
Высота основания правильной треугольной пирамиды равна 5 см, а двугранный угол при стороне основания равен 45°. Найдите:
а) площадь поверхности пирамиды;
б) расстояние от вершины основания до противоположной боковой грани.
Вариант 2
1. Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 и 3 см и углом В, равным 60°. Диагональ АС1, образует с плоскостью основания угол, равный 60°. Найдите площадь боковой поверхности призмы.
2. Сторона основания правильной треугольной пирамиды равна 3 см, а двугранный угол при стороне основания равен 45°. Найдите:
а) площадь поверхности пирамиды;
б) расстояние от вершины основания до противоположной боковой грани.

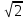 см,
см, 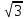 см.
см.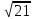 см. МК= РК. Найдите КМ, если расстояние от точки Е до прямой
см. МК= РК. Найдите КМ, если расстояние от точки Е до прямой 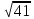 см.
см.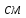 ,
, 



