
Тема урока:
«Перпендикулярные прямые в пространстве»
«Параллельные прямые, перпендикулярные к плоскости».
«Перпендикулярность прямой и плоскости»
Учитель МОУ СОШ №34
г. Комсомольска-на-Амуре
Есина Е.В.

Цели урока:
- Ввести понятие перпендикулярных прямых в пространстве;
- Доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой;
- Дать определение перпендикулярности прямой и плоскости;
- Доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярности к плоскости.

- Каково может быть взаимное расположение двух прямых на плоскости?
- Какие прямые в планиметрии называются перпендикулярными ?
а
в
а
а
в
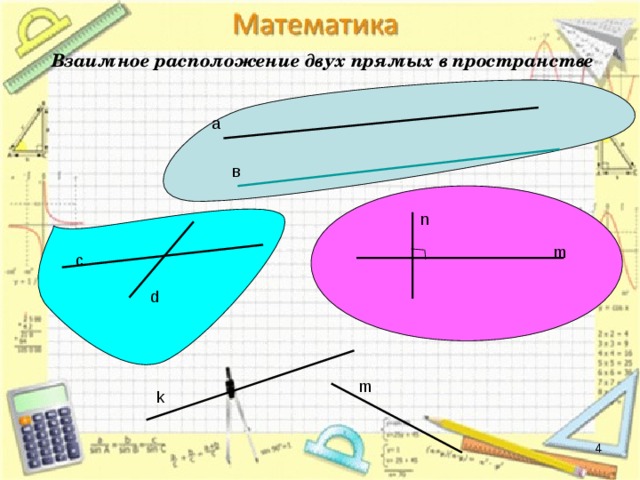
Взаимное расположение двух прямых в пространстве
а
в
n
m
с
d
m
k
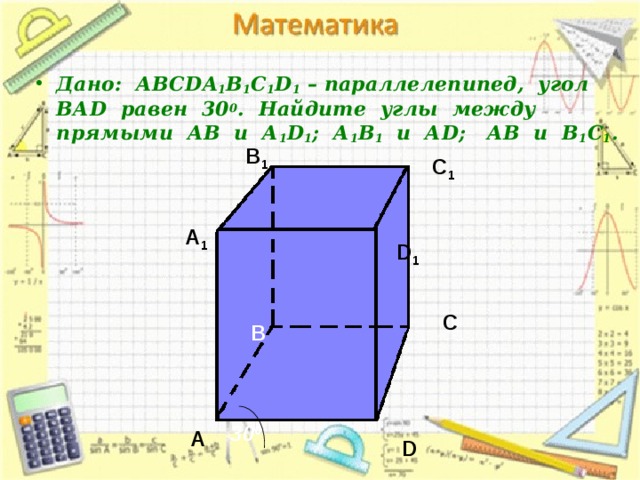
- Дано: АВС DA 1 B 1 C 1 D 1 – параллелепипед, угол ВА D равен 30 0 . Найдите углы между прямыми АВ и А 1 D 1 ; А 1 В 1 и А D ; АВ и В 1 С 1 .
В 1
С 1
А 1
D 1
С
В
30 0
А
D
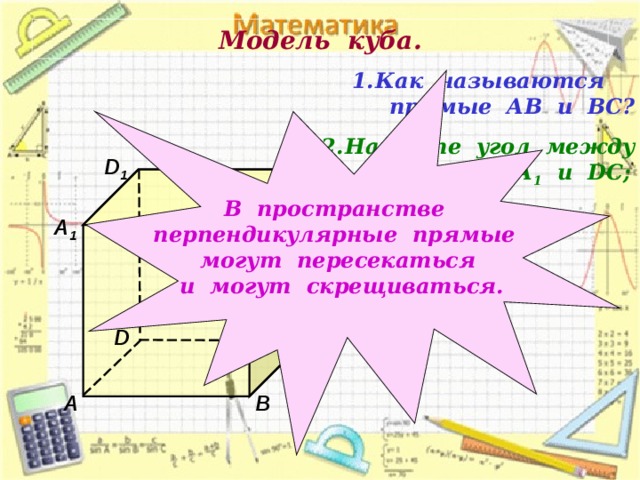
Модель куба.
- Как называются
прямые АВ и ВС?
В пространстве
перпендикулярные прямые
могут пересекаться
и могут скрещиваться.
- Найдите угол между
прямыми АА 1 и DC ;
ВВ 1 и А D .
D 1
С 1
В 1
А 1
D
С
А
В
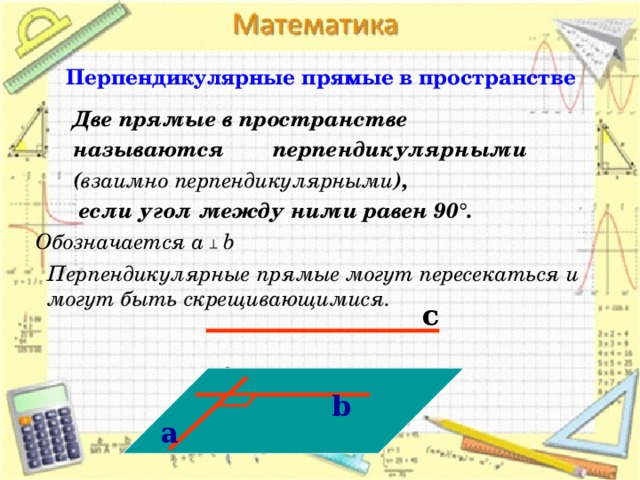
Перпендикулярные прямые в пространстве
Две прямые в пространстве
называются перпендикулярными
( взаимно перпендикулярными ),
если угол между ними равен 90 ° .
Обозначается a ┴ b
Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
c
b
а
7
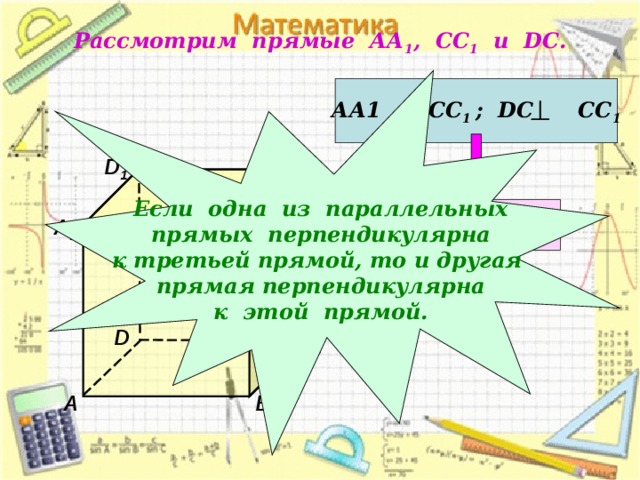
Рассмотрим прямые АА 1 , СС 1 и DC .
Если одна из параллельных
прямых перпендикулярна
к третьей прямой, то и другая
прямая перпендикулярна
к этой прямой.
АА1 ǁ СС 1 ; DC СС 1
D 1
С 1
АА 1 DC
А 1
В 1
D
С
А
В

Свойства :
1 . Если плоскость перпендикулярна одной
- из двух параллельных прямых,
- то она перпендикулярна другой
- прямой. ( a ⊥ α b и a II b = b ⊥ α )
- 2 . Если две прямые перпендикулярны
- одной и той же плоскости,
- то они параллельны. (a ⊥ α и b ⊥ α = a II b)
- 3 . Если прямая перпендикулярна
- одной из двух параллельных
- плоскостей, то она перпендикулярна
- и другой плоскости. ( α II β и a ⊥ α = a ⊥ β )
 a II β )" width="640"
a II β )" width="640"
Свойства :
- 4 . Если две различные плоскости
- перпендикулярны одной и той же прямой,
- то эти плоскости параллельны .
- (a ⊥ α и a ⊥ β = a II β )
- 5. Через любую точку пространства можно
- провести прямую, перпендикулярную
- данной плоскости, и притом только одну.
- 6. Через любую точку прямой можно
- провести плоскость, перпендикулярную ей
- и притом только одну.
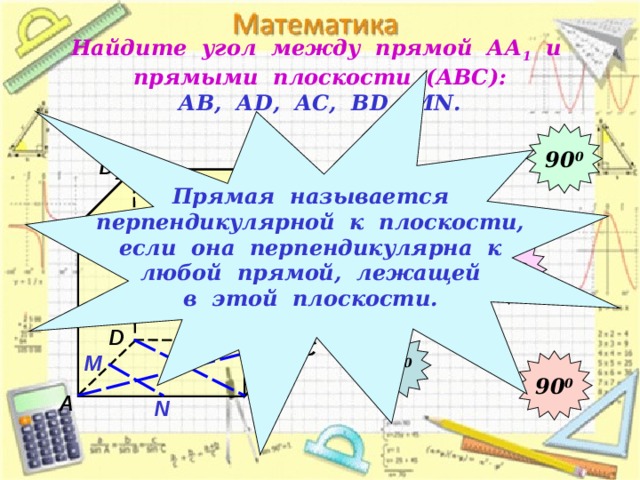
Найдите угол между прямой АА 1 и прямыми плоскости (АВС): АВ, А D , АС, В D , М N .
Прямая называется
перпендикулярной к плоскости,
если она перпендикулярна к
любой прямой, лежащей
в этой плоскости.
90 0
D 1
С 1
90 0
В 1
А 1
90 0
D
90 0
С
М
90 0
А
В
N
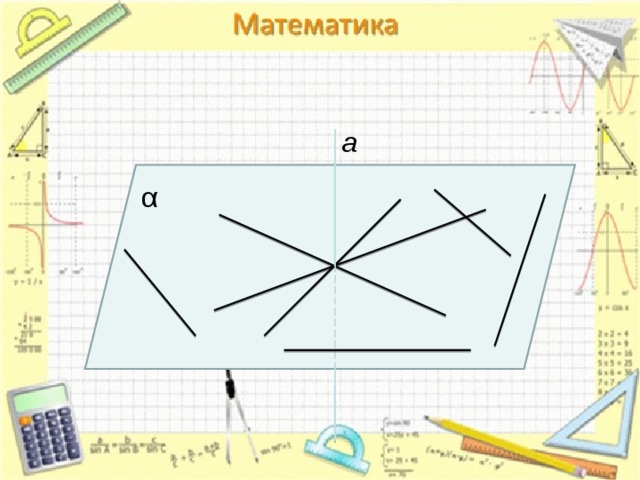
a
α
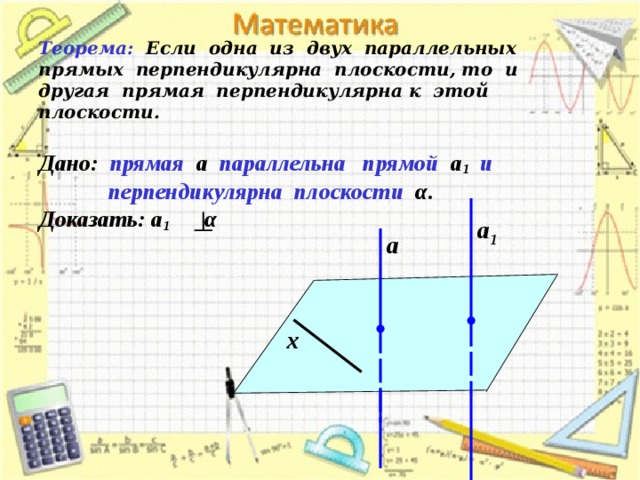
Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.
Дано: прямая а параллельна прямой а 1 и
перпендикулярна плоскости α .
Доказать: а 1 α
а 1
а
х

- Проведем прямую х в плоскости . Так как а , то а х. По лемме о перпендикулярности двух параллельных прямых к третьей а х. Т.о., прямая а1 перпендикулярна к любой прямой, лежащей в плоскости , т.е. а .
1
1
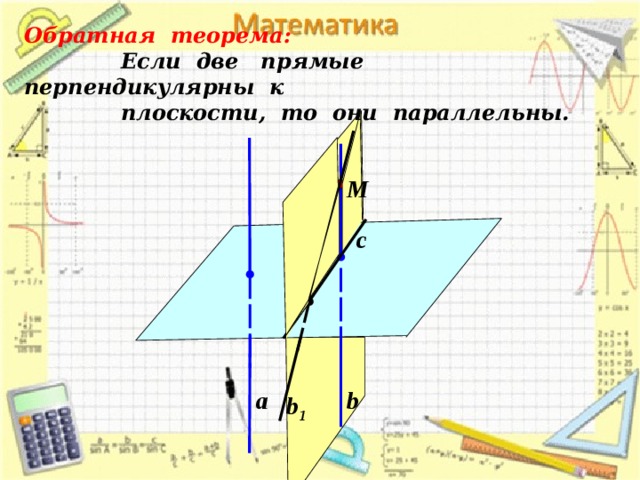
Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
M
c
b
а
b 1
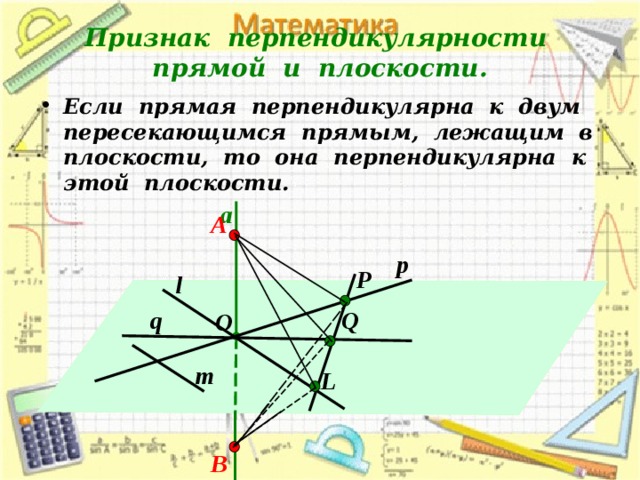
Признак перпендикулярности прямой и плоскости.
- Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
а
А
р
Р
l
q
Q
O
m
L
B
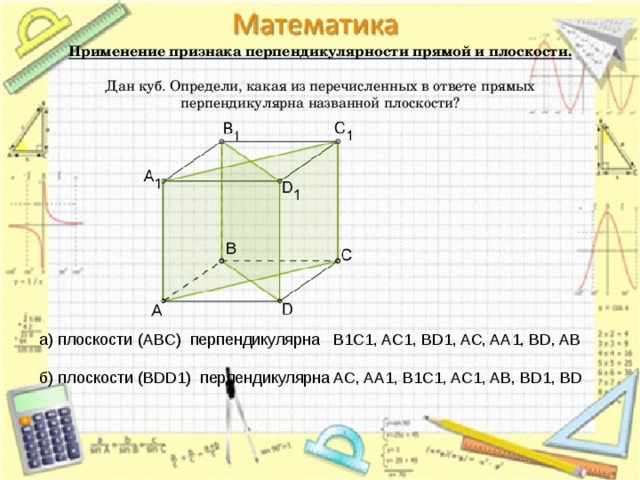
Применение признака перпендикулярности прямой и плоскости. Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?
а) плоскости (ABC) перпендикулярна B1C1, AC1, BD1, AC, AA1, BD, AB
б) плоскости (BDD1) перпендикулярна AC, AA1, B1C1, AC1, AB, BD1, BD
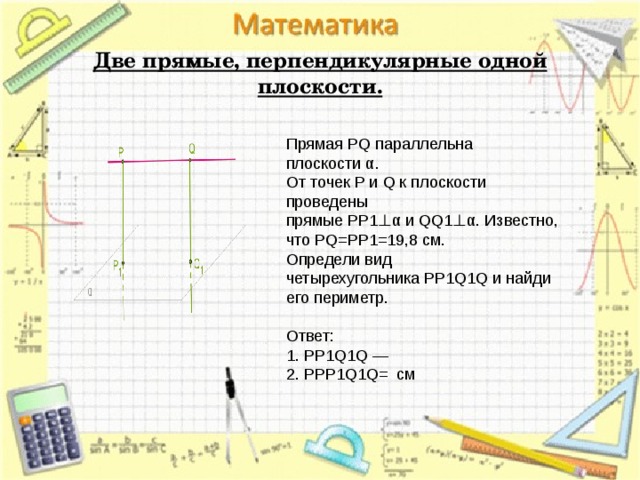
Две прямые, перпендикулярные одной плоскости.
Прямая PQ параллельна плоскости α.
От точек P и Q к плоскости проведены прямые PP1⊥α и QQ1⊥α. Известно, что PQ=PP1=19,8 см.
Определи вид четырехугольника PP1Q1Q и найди его периметр.
Ответ:
1. PP1Q1Q —
2. PPP1Q1Q= см
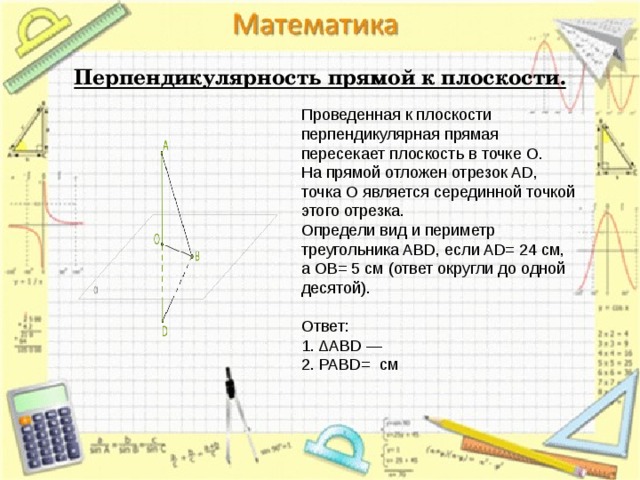
Перпендикулярность прямой к плоскости.
Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O.
На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка.
Определи вид и периметр треугольника ABD, если AD= 24 см, а OB= 5 см (ответ округли до одной десятой).
Ответ:
1. ΔABD —
2. PABD= см
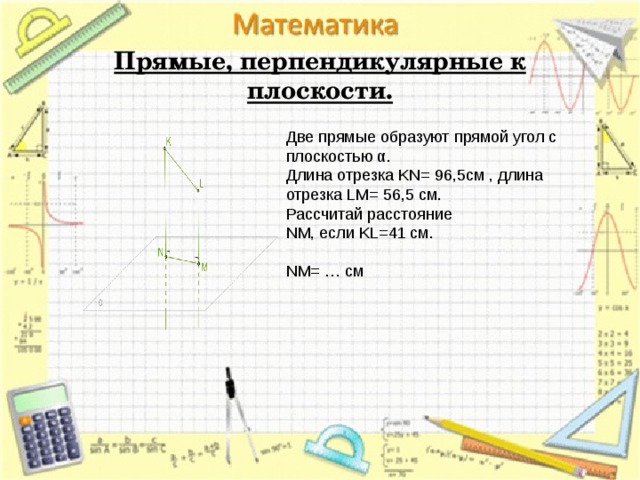
Прямые, перпендикулярные к плоскости.
Две прямые образуют прямой угол с плоскостью α.
Длина отрезка KN= 96,5cм , длина отрезка LM= 56,5 см.
Рассчитай расстояние NM, если KL=41 см.
NM= … см
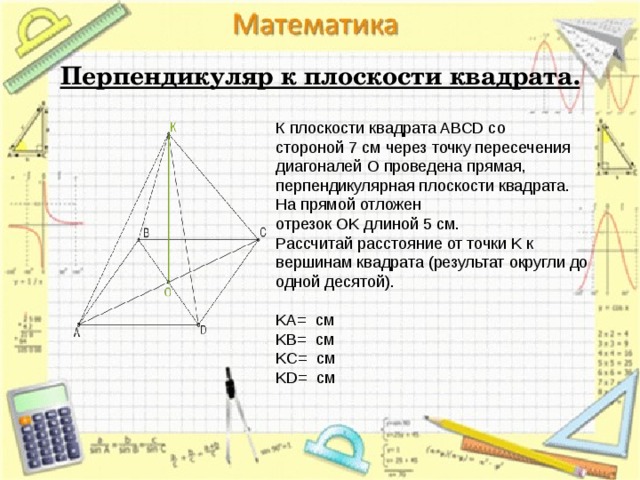
Перпендикуляр к плоскости квадрата.
К плоскости квадрата ABCD со стороной 7 см через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата.
На прямой отложен отрезок OK длиной 5 см.
Рассчитай расстояние от точки K к вершинам квадрата (результат округли до одной десятой).
KA= см
KB= см
KC= см
KD= см
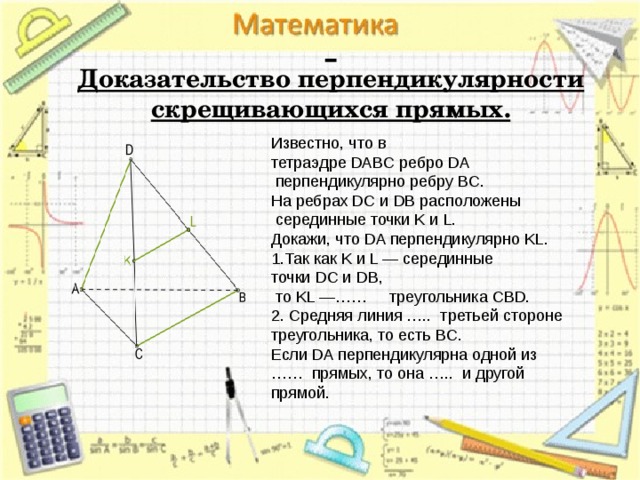
Доказательство перпендикулярности скрещивающихся прямых.
Известно, что в тетраэдре DABC ребро DA
перпендикулярно ребру BC.
На ребрах DC и DB расположены
серединные точки K и L.
Докажи, что DA перпендикулярно KL.
- Так как K и L — серединные точки DC и DB,
то KL —…… треугольника CBD.
2. Средняя линия ….. третьей стороне треугольника, то есть BC.
Если DA перпендикулярна одной из …… прямых, то она ….. и другой прямой.
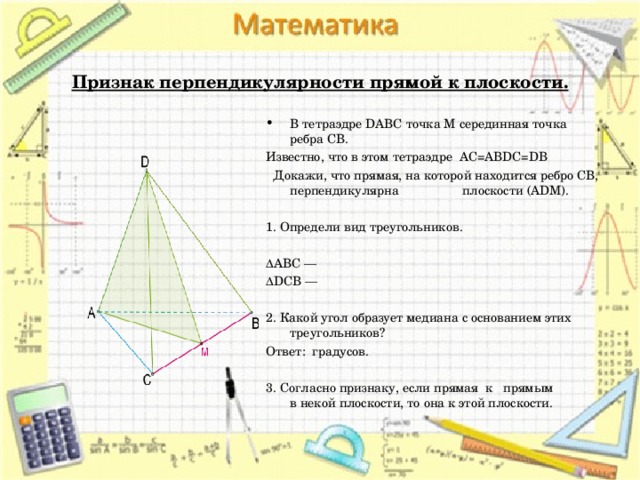
Признак перпендикулярности прямой к плоскости.
- В тетраэдре DABC точка M серединная точка ребра CB.
Известно, что в этом тетраэдре AC=ABDC=DB
Докажи, что прямая, на которой находится ребро CB, перпендикулярна плоскости (ADM).
1. Определи вид треугольников.
ΔABC —
ΔDCB —
2. Какой угол образует медиана с основанием этих треугольников?
Ответ: градусов.
3. Согласно признаку, если прямая к прямым в некой плоскости, то она к этой плоскости.
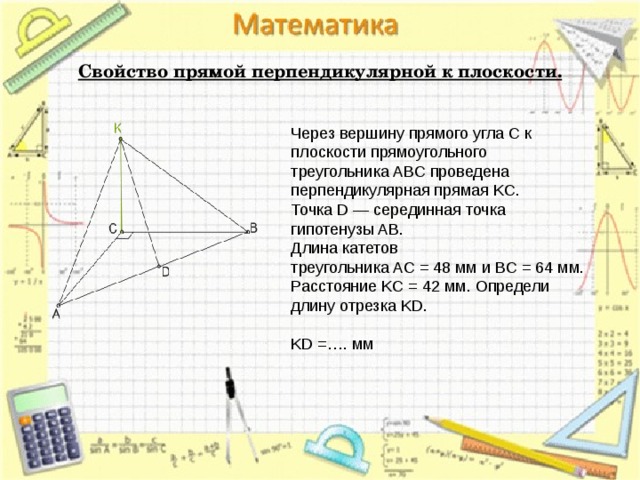
Свойство прямой перпендикулярной к плоскости.
Через вершину прямого угла C к плоскости прямоугольного треугольника ABC проведена перпендикулярная прямая KC.
Точка D — серединная точка гипотенузы AB.
Длина катетов треугольника AC = 48 мм и BC = 64 мм.
Расстояние KC = 42 мм. Определи длину отрезка KD.
KD =…. мм

(сложное) Доказательство от противного.
- Прямая d перпендикулярна плоскости α и прямой m, которая не лежит в плоскости α.
- Докажи, что прямая m параллельна плоскости α.
1. Согласно данной информации, если прямая не лежит в плоскости, она может или быть …плоскости, или … плоскость.
2. Допустим, что прямая m не ….., а …..плоскость α.
3. Если прямая d по данной информации перпендикулярна плоскости α, то она …… каждой прямой в этой плоскости, в том числе и прямой, которая проведена через точки, в которых плоскость пересекает прямые d и m.
4. Мы имеем ситуацию, когда через одну точку к прямой d проведены две …… прямые.
5. Это противоречие, из чего следует, что прямая m….. плоскости α, что и требовалось доказать.
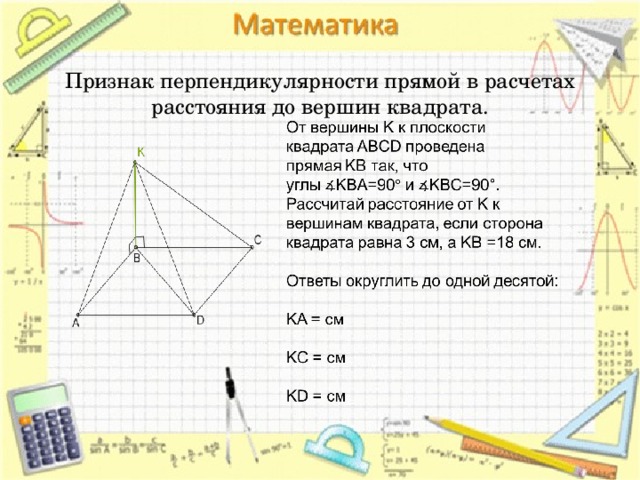
Признак перпендикулярности прямой в расчетах расстояния до вершин квадрата.
Домашнее задание
- П.15,16
Вопросы1,2 (стр.57)
№ 116,118





