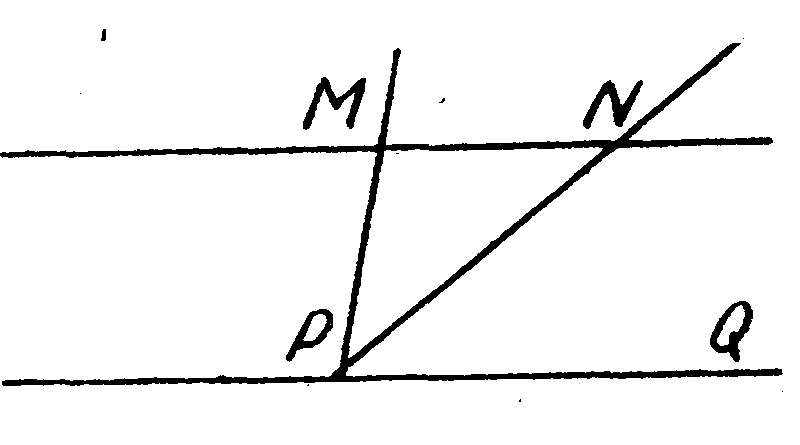Зачет по теме: "Параллельные прямые"

Фамилия Имя_________________________________________________7_____класс

ВАРИАНТ 1.

I.Заполните пропуски, чтобы получилось верное утверждение

1. Две прямые на плоскости называются параллельны­ми, если они _____________________________________.

2.1. Если при пересечении двух прямых секущей сумма _____________________________________углов равна 180°, то прямые параллельны.

2.2. Теорема обратная Теореме из 2.1______________________________________________________________ ________________________________________________________________________________________________

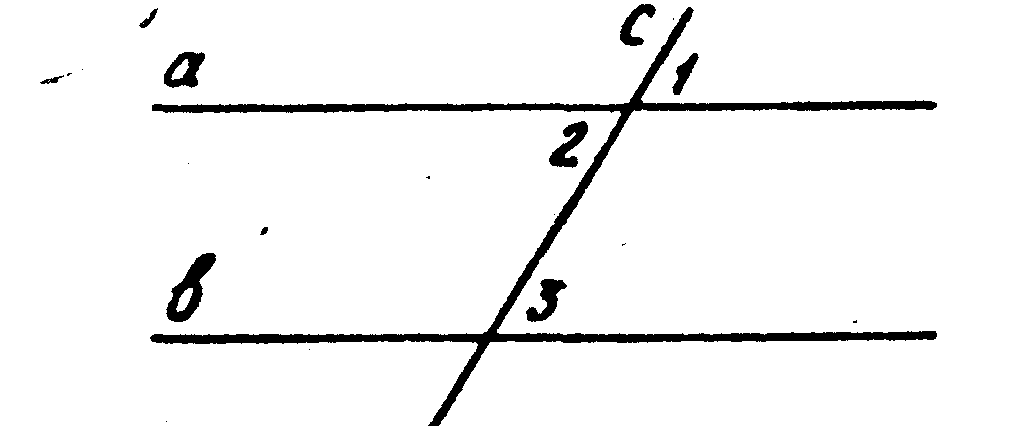
3. На рисунке а || b, с — секущая, тогда Ð1 ___Ð2, так как они _________________________________________.

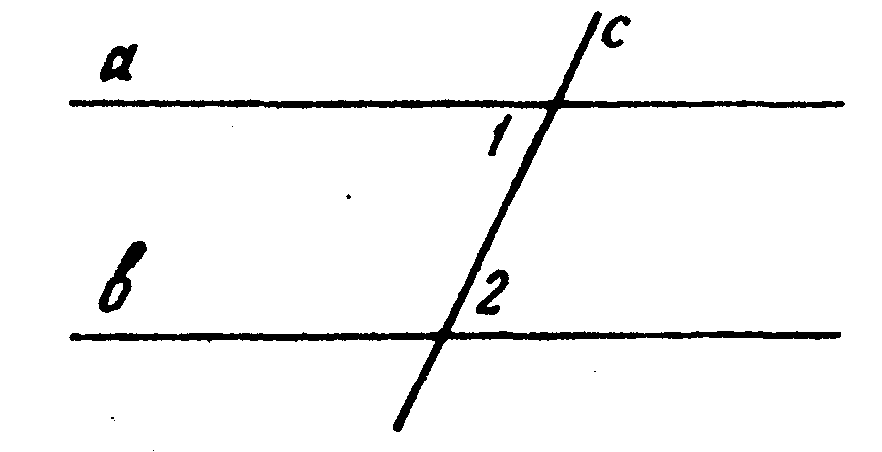
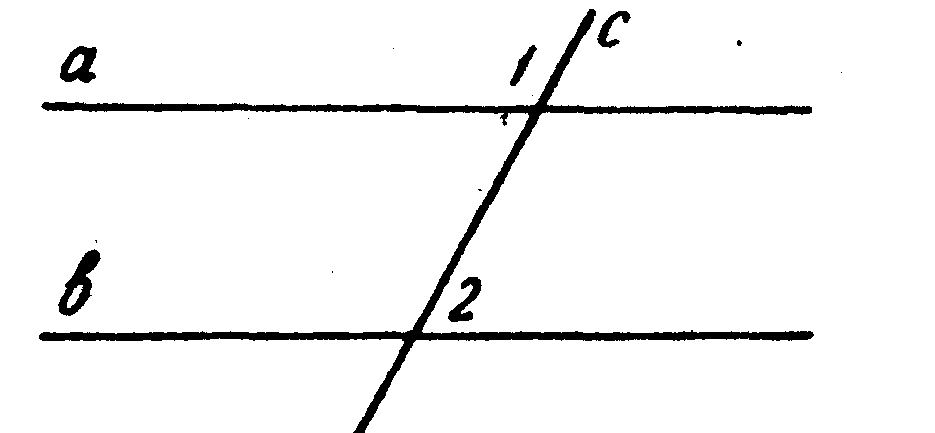
4. На рисунке Ð1=Ð 2, а это ________________________ при прямых _____и____ и секущей _____ _________

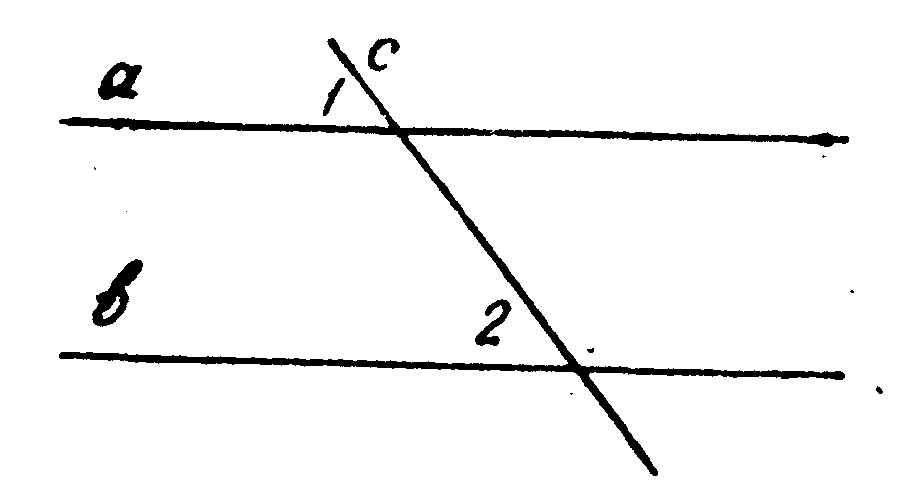
5. На рисунке m || n, р — секущая и Ðl + Ð2 = 240°, тогда Ð1= _______

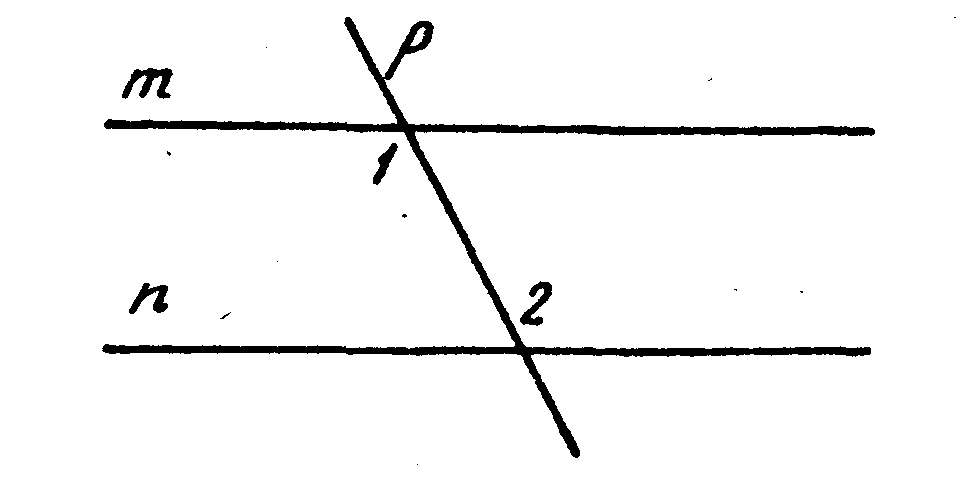
6. На рисунке а || b, Ð1 = 80°, тогда Ðl + Ð2 = _____, так как Ðl __Ð2 как ________________________________ углы при параллельных прямых _____и_____ и секущей ______

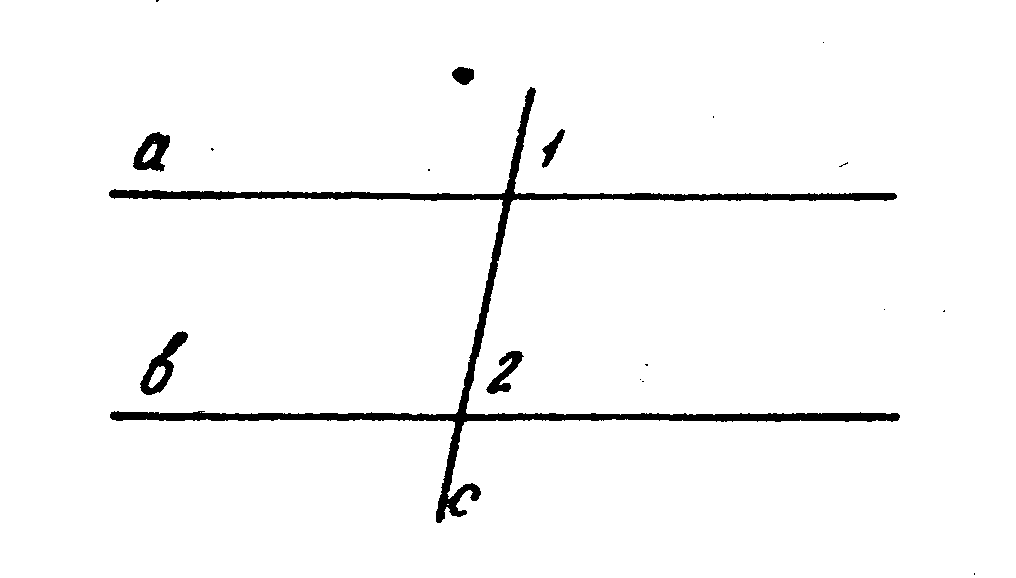
7. На рисунке а || b, с — секущая и Ð1 = 120°, тогда Ð2 =_____

II.Установите, истинны или ложны следующие утверждения (истинные обведите в кружок):

1. Две прямые на плоскости называются параллельными, если они не имеют общих точек.

2. Углы 4 и 6 накрест лежащие.

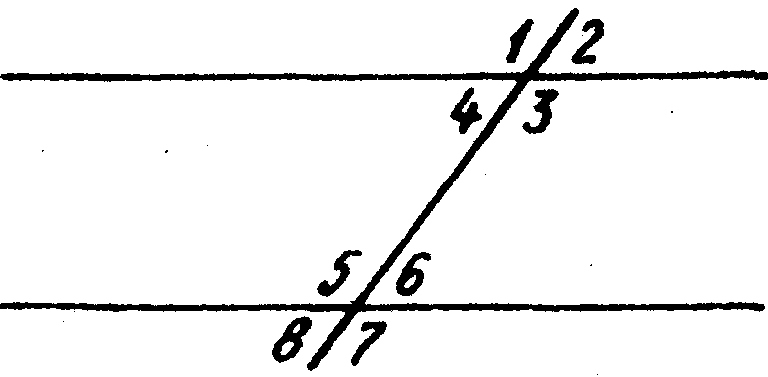
3. Если m || n, р -—секущая, тогда Ð1 + Ð2 =180°.

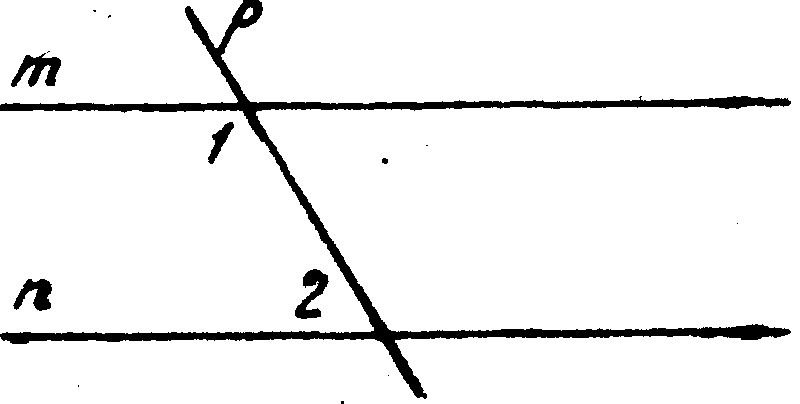
4. Если Ð1 =Ð2, тогда прямые а и b параллельны.

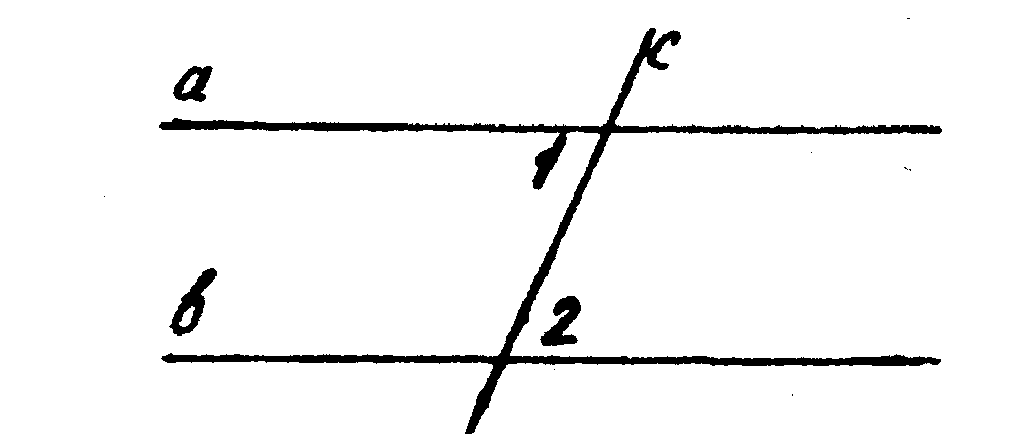
5. Если а || b, с — секущая и Ð1 + Ð2 = 190°, тогда Ð2 = 90⁰.

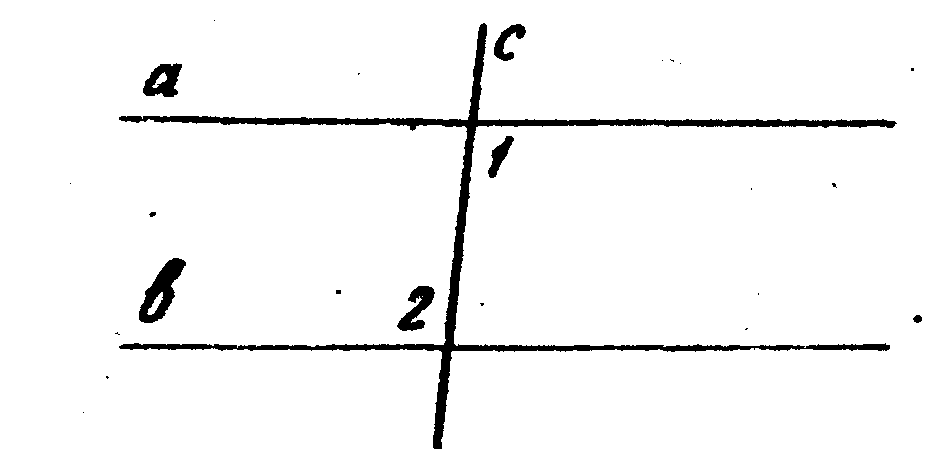
6. На рисунке m || n, р -— секущая, тогда Ðl = Ð2 (на чертеже покажи ход мыслей).

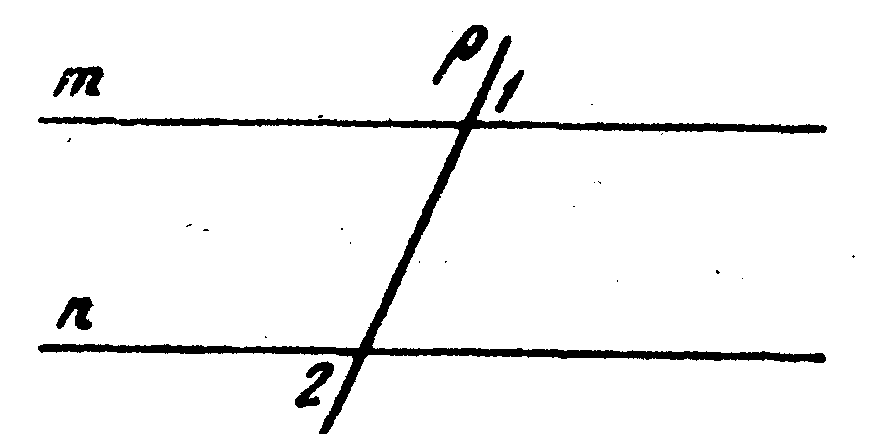
7. Два отрезка на плоскости называются параллельны­ми, если они не пересекаются.

8. На рисунке а || b, с — секущая и Ð1 + Ð2 = 120°, тогда Ð3 + Ð2 =120°.

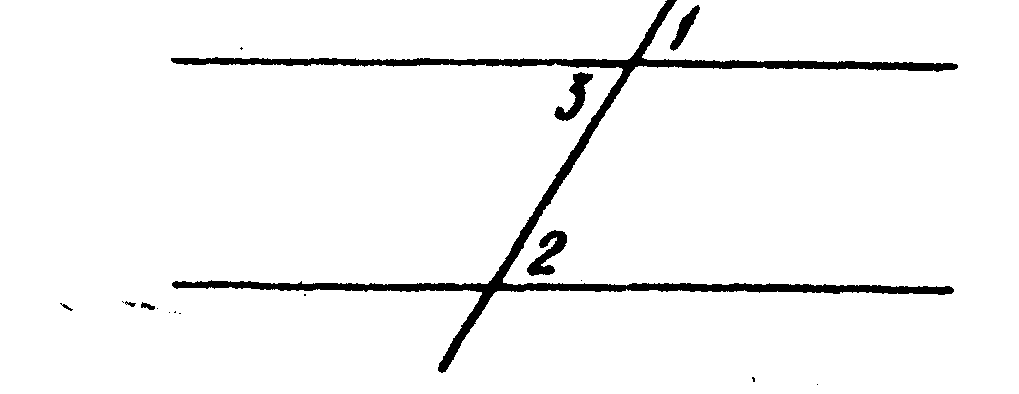
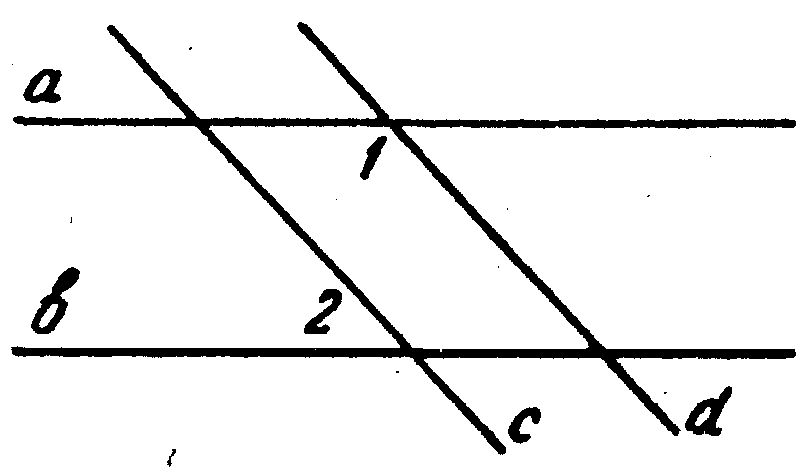
9. На рисунке а || b, с || d. Если Ð2 = 75°, то Ðl = 105° (Ответ обоснуй).

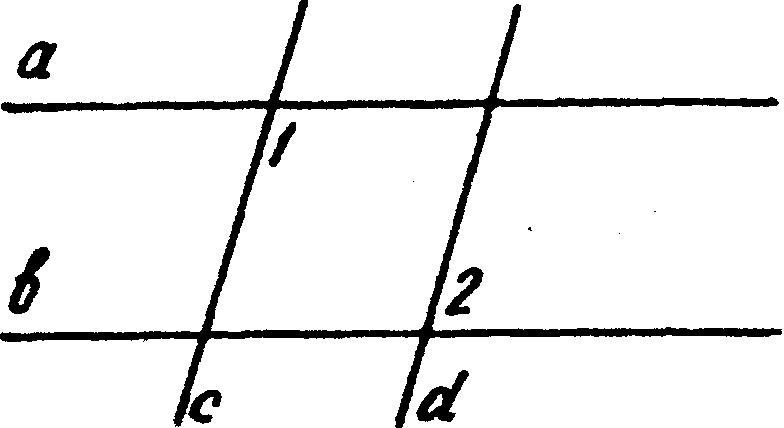
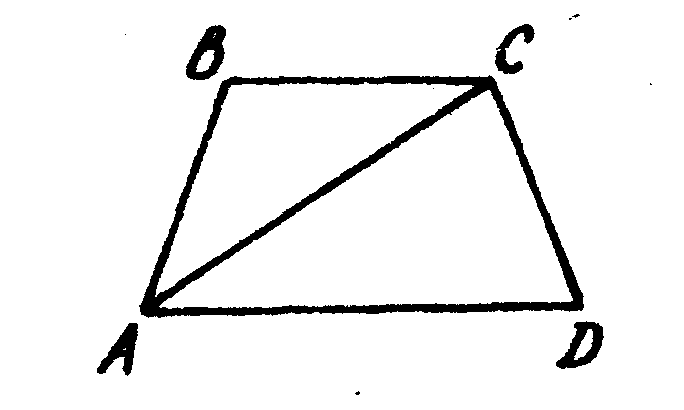
10. На рисунке AD || ВС. Если AВ = ВС, то ÐBAC = ÐCAD (на чертеже покажи ход мыслей)..

III.Решение задач:

1. При пересечении двух параллельных прямых третьей прямой сумма двух соответственных углов равна 100°. Найдите все образовавшиеся углы.

Дано:

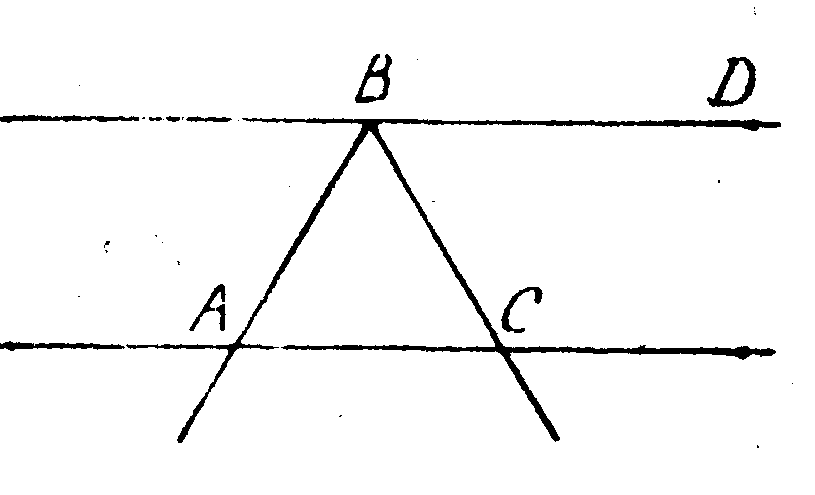
1. На рисунке BD || АС, луч ВС — биссектриса угла ABD, ÐCAB = 64°. Найдите угол ВСА.

Фамилия Имя_________________________________________________7_____класс

ВАРИАНТ 2

I.Заполните пропуски, чтобы получилось верное утверждение

1. Два отрезка называются параллельными, если они лежат на __________________________________ прямых.

2.1. Если две параллельные прямые пересечены секущей, то сумма ________________________________ углов равна 180°.

2.2. Теорема обратная Теореме из 2.1________________________________________________________________ _________________________________________________________________________________________________

3. На рисунке а || b, с — секущая, тогда Ð1 ___Ð2, так как они _________________________________________.

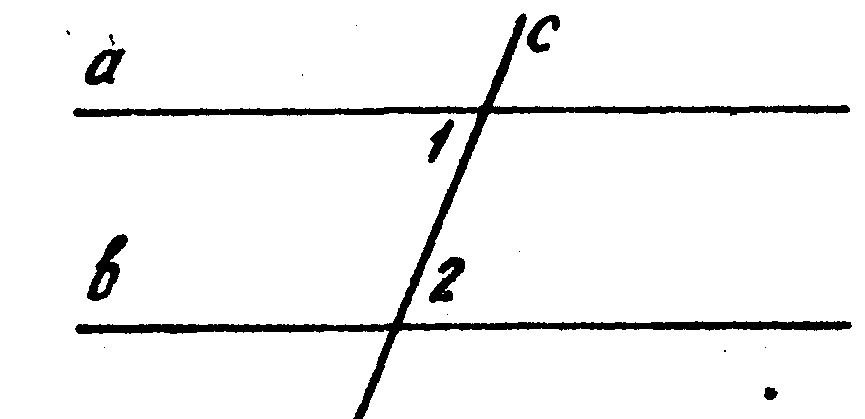
4. На рисунке Ðl = Ð2, а это _________________________ при прямых ____и____ и секущей _____ _________

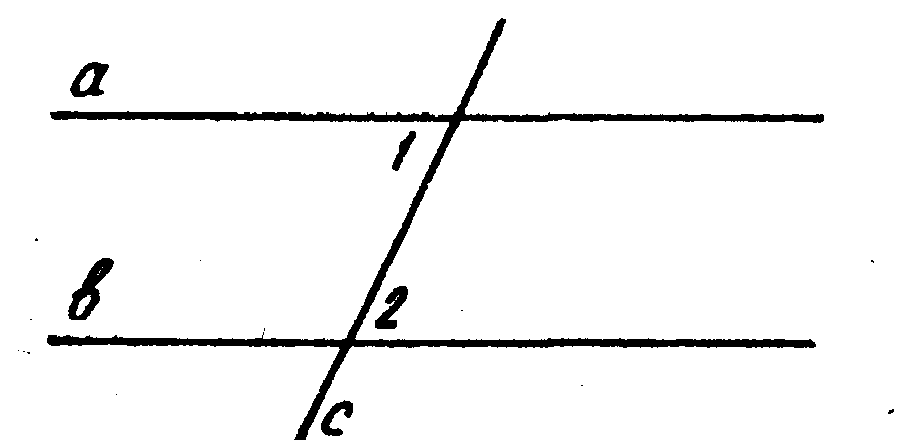
5. На рисунке а || b, с - секущая и Ðl + Ð2 = 240⁰, тогда Ð1= _______

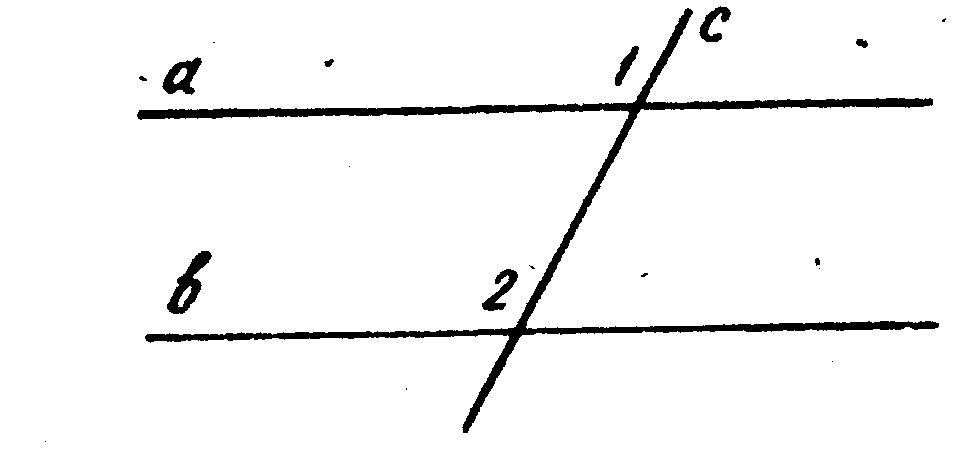
6. На рисунке а || b, с — секущая, Ð1 = 120°, тогда Ð1+Ð2= _____, так как Ðl __Ð2 , как ______________________ углы при параллельных прямых _____и_____ и секущей ____

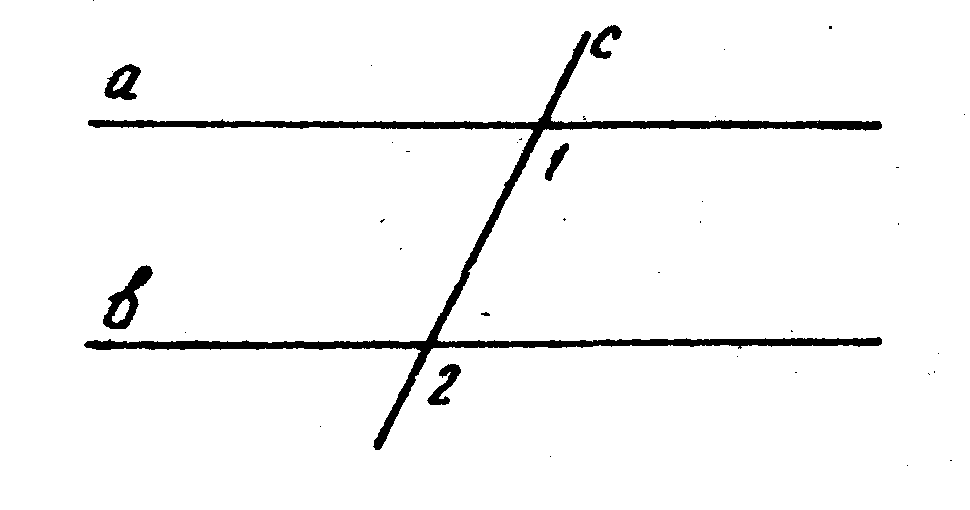
7. На рисунке m || n, р — секущая и Ð1= 80°, тогда Ð2 = ____

II.Установите, истинны или ложны следующие утверждения (истинные обведите в кружок):

1. Две прямые на плоскости называются параллельны­ми, если они не пересекаются.

2. На рисунке углы 3 и 6 односторонние.

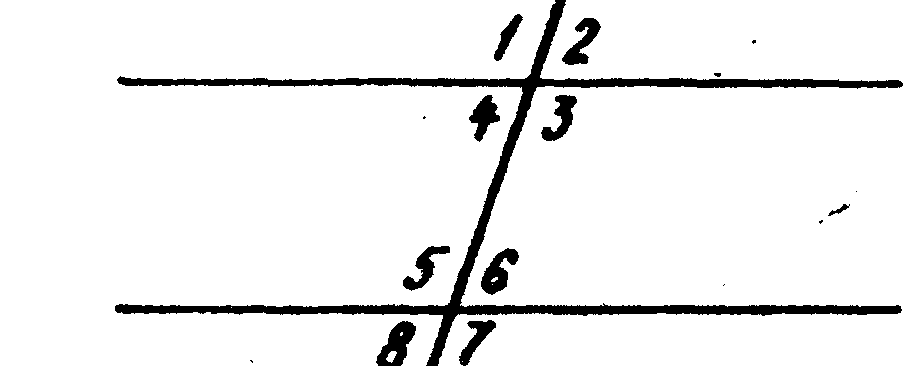
3. На рисунке а || b, с — секущая, тогда Ð1 = Ð2.

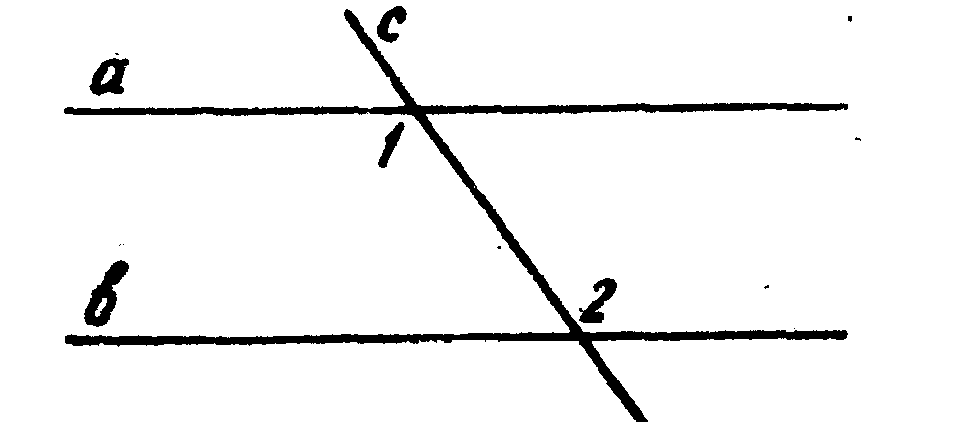
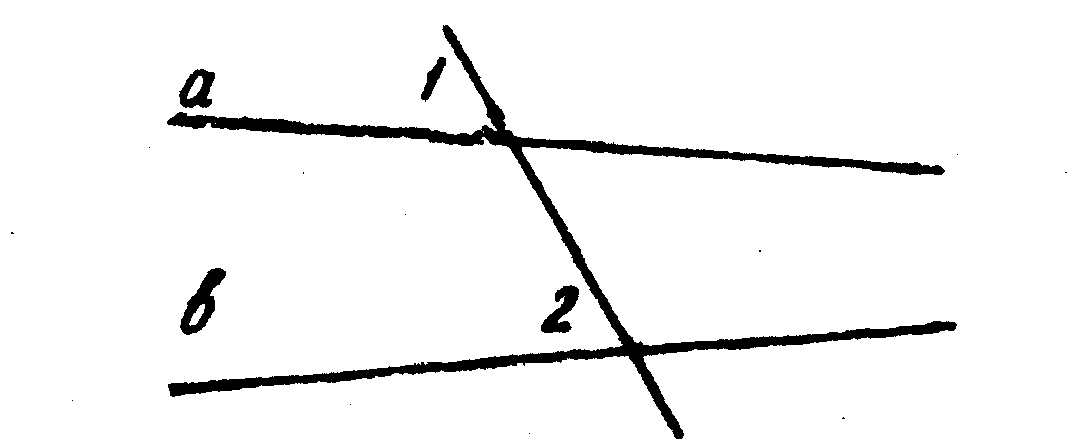
4. На рисунке Ðl =Ð2, тогда а || b.

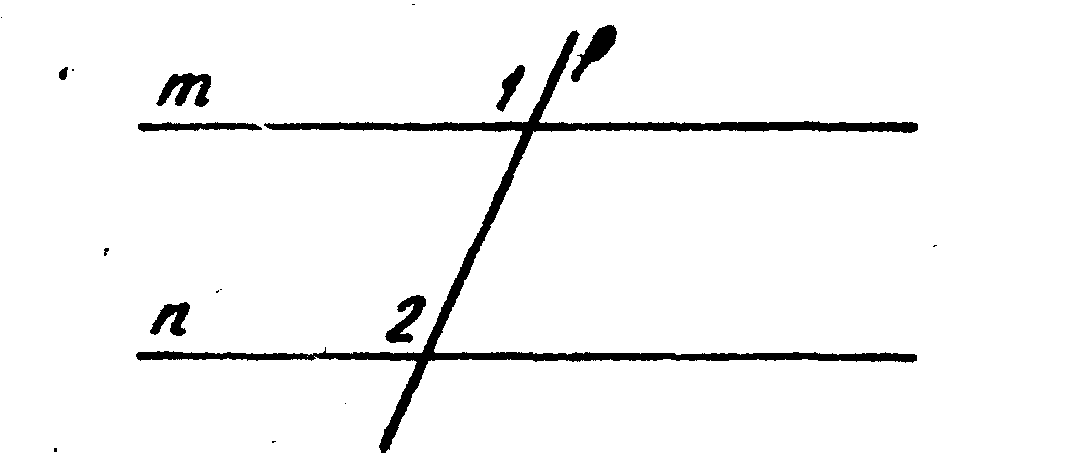
5. На рисунке m || n, р — секущая и Ðl + Ð2 =230°, тогда Ð1 = 115°.

6. На рисунке а || b, с — секущая, тогда Ðl = Ð2 (на чертеже покажи ход мыслей).

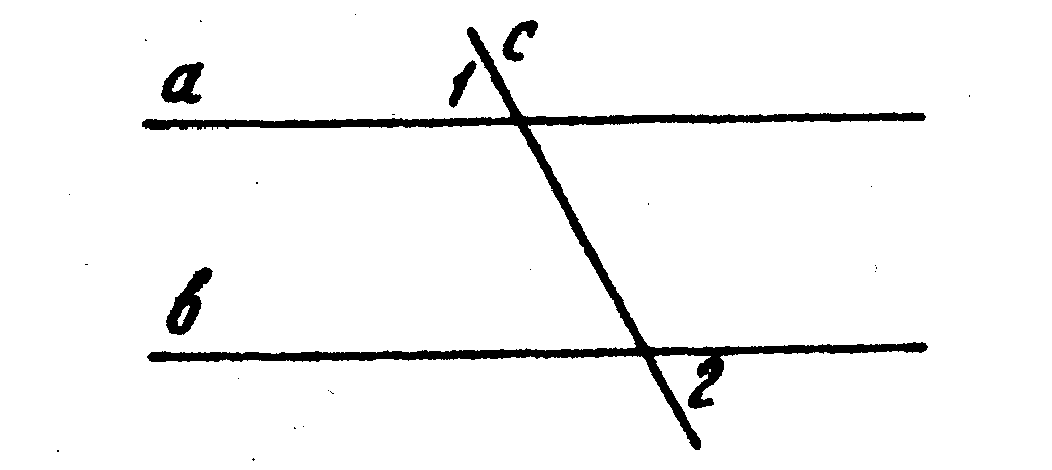
7. Если два отрезка не имеют общих точек, то они параллельны.

8. На рисунке а || b, с — секущая и Ð2 + Ð3 = 120°, тогда Ðl + Ð3 = 120°.

9. На рисунке а || b, с || d и Ðl = 135°, тогда Ð2 = 45°(Ответ обоснуй).

10. На рисунке MK || NP, NP =KP, тогда ÐPKN=ÐNKM (на чертеже покажи ход мыслей)..

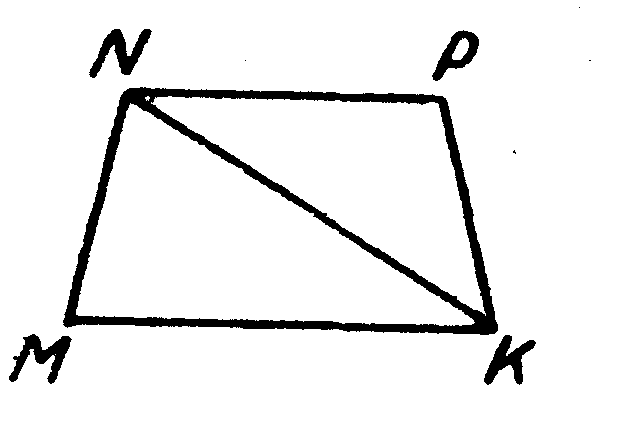
III.Решение задач:

1. При пересечении двух параллельных прямых третьей прямой сумма двух накрест лежащих углов равна 130°. Найдите все образовавшиеся углы.

Дано:

1. На рисунке MN || PQ, луч PN — биссектриса угла MPQ, ÐNPQ = 40°. Найдите угол PMN.