
Цилиндр

Цели урока:
- Ввести понятия цилиндрической поверхности, цилиндра и его элементов;
- Вывести формулы для вычисления площадей боковой и полной поверхностей цилиндра;
- Рассмотреть типовые задачи по теме.

Определение:
- Тело, ограниченное цилиндрической поверхностью и двумя кругами, называется цилиндром .
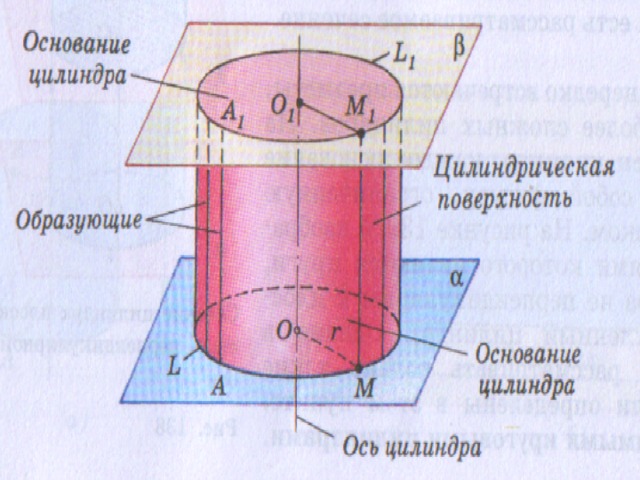

Общие понятия
- Цилиндрическая поверхность называется боковой поверхностью цилиндра , а круги – основаниями цилиндра.
- Образующие цилиндрической поверхности называются образующими цилиндра .
- Прямая проходящая через центры оснований называется осью цилиндра .
- Длина образующей называется высотой , а радиус основания – радиусом цилиндра .
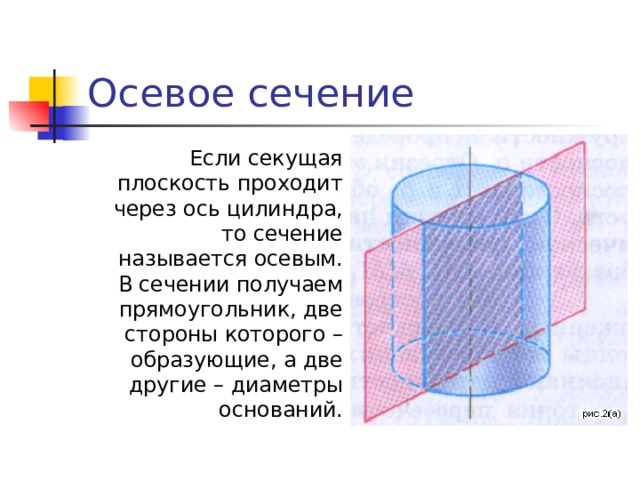
Осевое сечение
Если секущая плоскость проходит через ось цилиндра, то сечение называется осевым. В сечении получаем прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований.
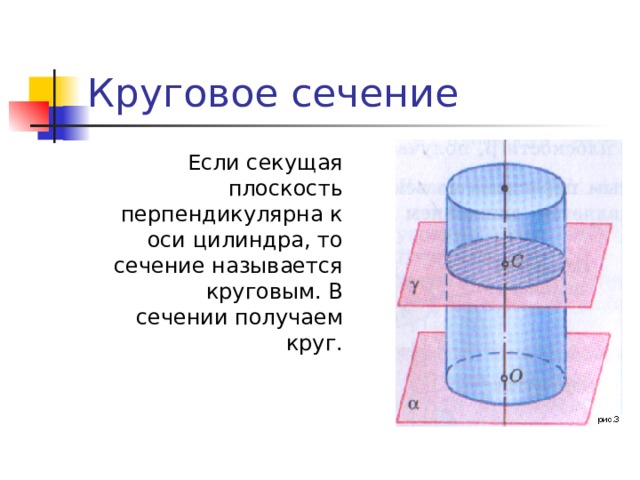
Круговое сечение
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение называется круговым. В сечении получаем круг.
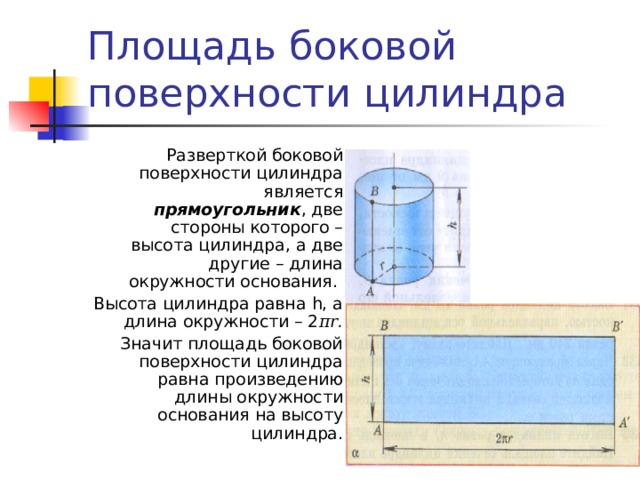
Площадь боковой поверхности цилиндра
Разверткой боковой поверхности цилиндра является прямоугольник , две стороны которого – высота цилиндра, а две другие – длина окружности основания.
Высота цилиндра равна h , а длина окружности – 2 π r .
Значит площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

Площадь полной поверхности цилиндра
Площадь полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна π r 2 , то для вычисления площади полной поверхности цилиндра получаем формулу:

Решение задач:
- Подведение итогов, домашнее задание:
- п.п. 53,54
- №№ 527, 531
№№ 530, 537





