

ОПРЕДЕЛЕНИЕ.
Геометрическое тело или многогранник, состоящий из трёх пар равных паралле- лограммов лежащих в парал-
лельных плоскостях, называ-
ется параллелепипедом
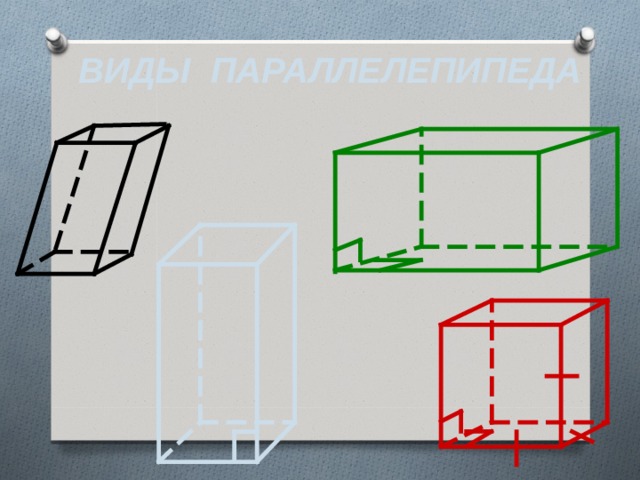
ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
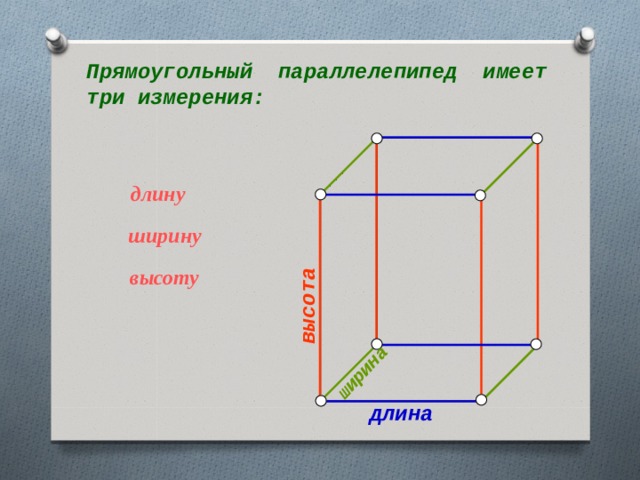
ширина
высота
Прямоугольный параллелепипед имеет три измерения:
длину
ширину
высоту
длина
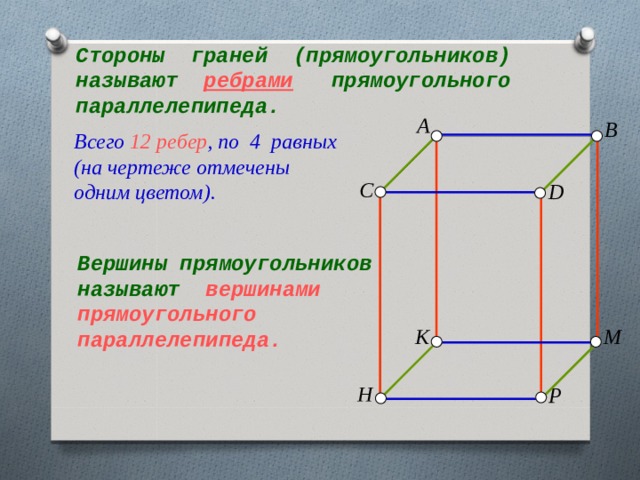
Стороны граней (прямоугольников) называют ребрами прямоугольного параллелепипеда.
A
B
Всего 12 ребер , по 4 равных (на чертеже отмечены одним цветом).
C
D
Вершины прямоугольников называют вершинами прямоугольного параллелепипеда.
M
K
H
P

ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямо-
угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
C 1
D 1
B 1
A 1
D
С
В
А
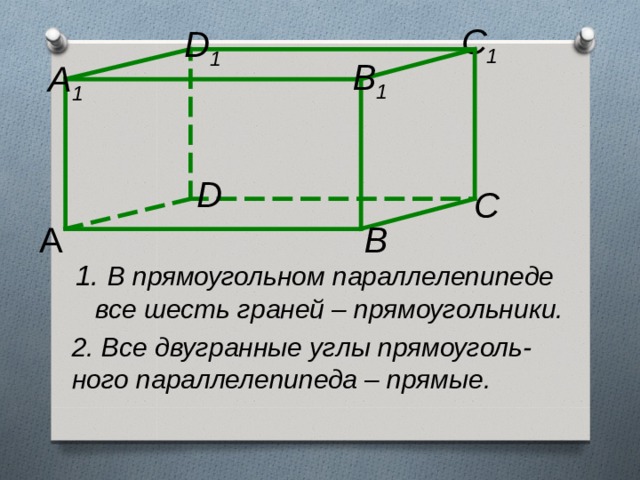
- В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2. Все двугранные углы прямоуголь- ного параллелепипеда – прямые.

C 1
D 1
Доказать:
AC 1 2 =AB 2 +AD 2 +AA 1 2
B 1
A 1
Доказательство:
1 . ABD – прямоугольный
По т. Пифагора
DB 2 =AB 2 +AD 2
D
2. BDD 1 –
прямоугольный
По т. Пифагора
BD 1 2 =BD 2 +DD 1 2
С
В
А
3 . Из 1 и 2 следует: AC 1 2 =AB 2 +AD 2 +AA 1 2
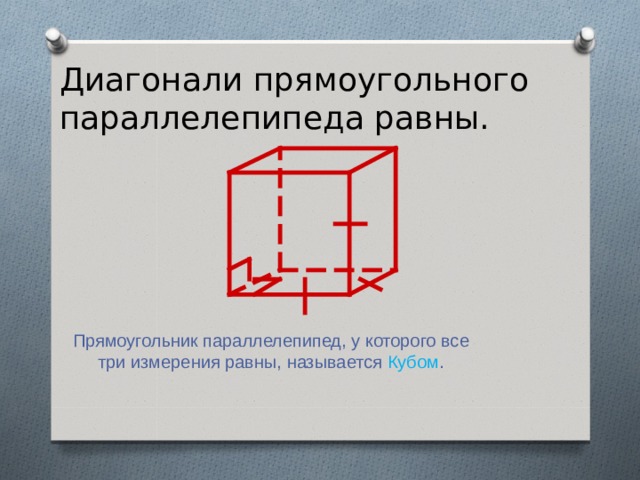
Диагонали прямоугольного параллелепипеда равны.
Прямоугольник параллелепипед, у которого все три измерения равны, называется Кубом .
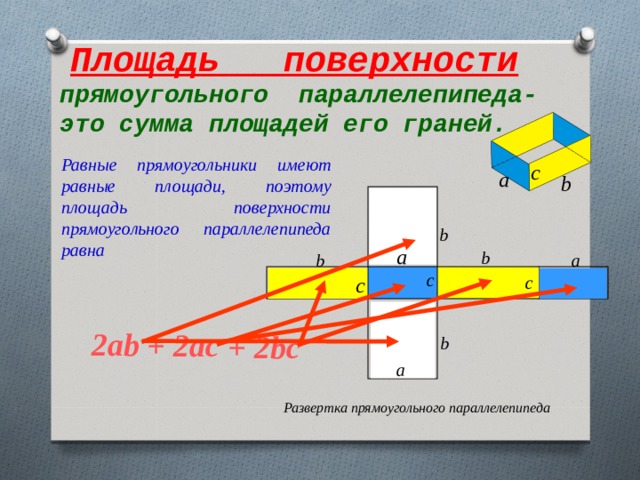
Площадь поверхности
прямоугольного параллелепипеда-это сумма площадей его граней.
Равные прямоугольники имеют равные площади, поэтому площадь поверхности прямоугольного параллелепипеда равна
c
a
b
b
a
b
а
b
c
с
c
2ab
+ 2ac
+ 2bc
b
а
Развертка прямоугольного параллелепипеда
10
Примеры предметов, имеющих форму прямоугольного параллелепипеда
11





