Урок по геометрии "Теорема Пифагора"

УМК	Атанасян Л. С, Бутузов В. Ф., Кадомцев СБ., Юдина И. И. Геометрия. 8, Москва, Просвещение, 2008.
Класс	8
Тема урока	«Теорема Пифагора»
Тип урока	Открытие нового знания
Цели урока для учителя:	· формирование понятий: «прямоугольный треугольник», «свойства прямоугольного треугольника», «площадь фигур», «свойства площадей», «Теорема Пифагора» - формирование логического мышления путём применения приёмов сравнения, анализа, выделения главного · формирование умения воспринимать и применять информацию, самостоятельно определять задачи учебной деятельности · формирование смыслов учебной деятельности на основе развития познавательного интереса
Цели урока для обучающихся:	· вспомнить понятия: «прямоугольный треугольник», «свойства прямоугольного треугольника», «площадь фигур», «свойства площадей», · открыть понятие «Теорема Пифагора» · работать в группе и паре · формулировать и аргументировать свою точку зрения · решать задачи по теме по алгоритму.
Методическая цель:	Проектирование современного урока математики с учётом ФГОС ООО
Средства реализации методической цели:	Совместное целеполагание, планирование деятельности на уроке; самостоятельная оценочная деятельность; проблемная ситуация; индивидуальные и парные задания; рефлексия.
Формируемые универсальные учебные действия
Познавательные УУД	· формулирование проблемы; · самостоятельное создание способов решения проблем; · осознанное построение речевого высказывания; · умение осуществлять сравнение, устанавливать причинно-следственные связи; · алгоритмизация способа действия.
Регулятивные УУД	· целеполагание; · планирование; · контроль и оценка деятельности на учебном занятии.
Личностные УУД	· развитие адекватной самооценки; · развитие познавательных интересов, учебных мотивов; · взаимопомощь.
Коммуникативные УУД	· формулирование и аргументация собственного мнения; · умение договариваться и приходить к общему решению; · умение строить монологическое высказывание.

Ход учебного занятия

Этапы урока	Виды деятельности	Формируемые УУД
Мотивационно-установочный этап	· целеполагание · самоопределение · постановка проблемного вопроса · планирование работы на уроке	· личностные ·коммуникативные · познавательные
Операционно – познавательный этап	· диалог, подводящий к новому знанию · работа в парах, взаимопомощь · взаимооценивание и самооценивание результата	· познавательные ·коммуникативные · регулятивные · личностные
Контрольно-регулировочный этап.	· ответ на проблемный вопрос · анализ, сравнение, обобщение - взаимопроерка по эталону · фронтально-индивидуальная работа · самоконтроль и самооценка индивидуальных и парных заданий · выполнение действий по алгоритму	· познавательные · регулятивные ·коммуникативные
Рефлексивно-оценочный этап	· понимание причин успеха/неуспеха · самооценка	· личностные · регулятивные ·коммуникативные

Ход урока

I. Мотивационно – установочный этап.

Цель этапа:

1. Включить учащихся в учебную деятельность;

2. Определить содержательные рамки урока;

3. Организовать коммуникативное взаимодействие,

1) Организационный момент.

Слайд №1.

- Здравствуйте, ребята! Улыбнитесь друг другу, пожелайте успехов.

- Ответьте, пожалуйста, на вопрос: где и когда мы используем знания, полученные на уроках геометрии? А можно обойтись без этих знаний в жизни?

- На партах перед каждым из вас стоят две коробочки и прямоугольники, вырезанные из бумаги. На одной коробочке написано ЗНАЮ, на другой НОВЫЕ ЗНАНИЯ. Договоримся с вами, что когда вы услышите вопрос, на который знаете ответ, будете опускать в коробочку «ЗНАЮ» прямоугольник, а если узнаете что-то впервые, опустите прямоугольник в коробочку с «НОВЫМИ ЗНАНИЯМИ». Также у каждого из вас есть лист самооценки, не забывайте ставить себе оценку на каждом этапе урока.

2) Формулировка темы урока темы.

Слайд №2.

Разгадывание кроссворда. Работа в парах. Самопроверка по эталону.

Угадав все слова и записав их в клеточки по гори­зонтали, в выделенном вертикальном столбце вы про­чтете фамилию известного ученого-математика Древ­ней Греции.

По горизонтали: 1. Отрезок прямой, образующий прямой угол с данной прямой и имеющий одним из своих концов их точку пересечения, есть … к данной прямой. 2. Элемент прямоугольного треугольника. 3. Треугольник есть геометрическая … . 4. Отрезок, соединяющий вершину треугольника с серединой про­тивоположной стороны. 5. Два луча, исходящие из одной точки. 6. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 7. Замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки О. (Пифагор) Самопроверка. Оценки выставить в оценочный лист.

- Как вы думаете, какая же тема нашего урока?

- Тема нашего урока «Теорема Пифагора». Запишите её в свои тетради.

Слайд №3.

- Скажите, глядя на эту тему, что – нибудь вам знакомо? Что бы вы хотели узнать по этой теме?

3) Составление плана урока.

• Формулировка теоремы и её доказательство.

• Применение теоремы.

• Биография Пифагора.

• Применение теоремы к решению задач.

Но прежде чем мы приступим к изучению нового материала, покажите мне знания, которые нам необходимы для этого.

4) Актуализация опорных знаний.

Слайд 4.

- Какая геометрическая фигура изображена на экране?

НЕЗАБЫВАЙТЕ ПРО КОРОБОЧКИ СО ЗНАНИЯМИ!

- Как определили что это прямоугольный треугольник?

- Кто может дать полное определение прямоугольного треугольника?

Слайд 5.

- Какой треугольник изображен сейчас?

Продолжите предложение:

Слайд 6.

- Сторона, лежащая против угла 90^о называется ...

- Стороны образующие прямой угол называются….

Вспомним некоторые свойства прямоугольного треугольника:

Слайд 7.

- Сумма острых углов …..

Слайд 8.

- Катет, лежащий против угла в 30⁰ равен …

Посмотрим, что вы помните о свойствах площадей:

Слайд 9.

- Равные многоугольники имеют ...

- Если многоугольник составлен из нескольких многоугольников, то его площадь равна ...

- Площадь квадрата равна ...

Слайд 10.

- Площадь прямоугольного треугольника равна….

Открытие новых знаний.

1)Создание проблемной ситуации.

Слайд 11.

- А теперь давайте решим небольшую задачу.

Задача 1. Велосипедист и пешеход отправились одновременно из одного населенного пункта в разных направлениях. Пешеход пошел на восток со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч. Какое расстояние будет между ними через час?

Задача 2. Велосипедист и пешеход отправились одновременно из одного населенного пункта в разных направлениях. Пешеход пошел на юг со скоростью 5 км/ч, а велосипедист поехал на запад со скоростью 12 км/ч. Какое расстояние будет между ними через час?

- Начертите в тетрадях схему движения пешехода и велосипедиста.

- Какая фигура получилась?

- Какие стороны известны?

- Что нужно найти?

Тех знаний о прямоугольном треугольнике, которые мы имеем, не хватает. Последнюю задачу решить не можем.

2) Постановка учебной задачи урока.

- Сформулируйте то, что мы должны знать, чтоб решить эту задачу?

- Это и будет цель нашего урока.

3) Сообщение главной цели урока.

- Цель нашего урока как раз и заключается в том, чтобы выяснить, как связаны между собой стороны прямоугольного треугольника.

II. Операционно – познавательный этап.

1) Открытие теоремы Пифагора. Исследовательская деятельность.

Работа в парах

Слайд 12.

- Чтобы это выяснить, мы займемся исследовательской деятельностью.

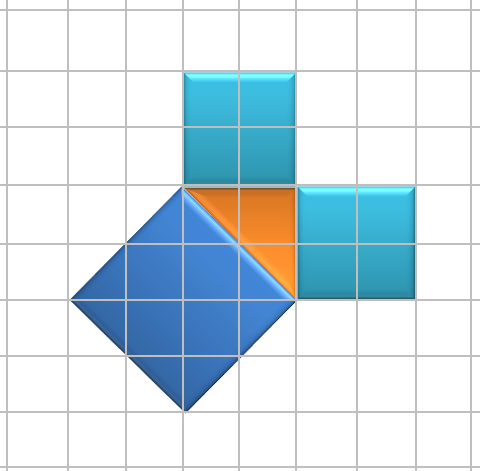
- Я вам раздам лист, на котором оранжевым цветом закрашен равнобедренный прямоугольный треугольник, на сторонах которого построены квадраты. Ответьте на два вопроса и сделайте вывод.

с a b

Найдите площади квадратов построенных на сторонах данного равнобедренного прямоугольного треугольника. Сравните площадь квадрата построенного на стороне с и площади двух остальных квадратов Сделайте вывод

Слайд 13.

Вывод: Площадь квадрата построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

Так изначально формулировалась теорема Пифагора.

Слайд 14.

- Сейчас теорема звучит так: Квадрат гипотенузы равен сумме квадратов катетов.

- Ребята! Утверждение, которое вы только что сформулировали, является одной из важнейших теорем геометрии и имеет своё имя – теорема Пифагора

2) Историческая справка.

Слайд 15.

1. Работа в группе.

- Найдите в справочной литературе или интернете ответы на следующие вопросы:

1 группе нужно подготовить материал о биографии Пифагора.

2 группе - о школе Пифагора.

2. Проверка домашнего задания. Заранее подготовленный ученик рассказывает об истории теоремы Пифагор.

3) Доказательство теоремы Пифагора

Видео

- А сейчас посмотрим на доказательство теоремы. Видео ресурс из ЦОР (1 мин.)

- Формулировку теоремы давайте запишем в тетрадь. (Квадрат гипотенузы равен сумме квадратов катетов.)

Динамическая пауза для глаз. Слайд 16,17,18

- Напоминаю, чтобы вы не забывали о «коробочках со знаниями»!

4) Применение теоремы Пифагора.

- А сейчас давайте посмотрим видеоролик о применении теоремы Пифагора.

Видео Видеоролик мультяшной формы из интернета (1,5 мин)

III. Контрольно – регулировочный этап.

1)Первичное закрепление изученного материала.

Решение задач по готовым чертежам.

- Мы доказали с вами одну из важнейших теорем геометрии. Давайте попробуем решить с её помощью несколько задач по готовым чертежам устно.

Слайд 19.

1.Найдите гипотенузу с прямоугольного треугольника по данным катетам а и в если: а = 6, в = 8

2. В прямоугольном треугольнике а и в катеты, с – гипотенуза. Найдите в, если с = 13, а = 12.

Слайд 20.

- Вернёмся теперь к задаче, которую мы не смогли решить в начале урока.

- Запишите решение в своих тетрадях.

Слайд 21.

- Решим древнюю индийскую задачу о тополе.

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Слайд 22.

- Рассмотрим условие еще одной древней задачи:

Случится некому человеку к стене лестницу прибрати , стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстоятиимать.

Самостоятельная работа с взаимопроверкой по эталону.

Слайд 23.

Разноуровненвая самостоятельная работа.

- Выберите ту ступеньку с задачей, которую вы сможете решить.

Слайд 24.

Проверка по эталону.

- Поменяйтесь тетрадями.

- Посмотрите на слайд и проверьте решение, поставьте оценки соответствующие вашей ступеньки.

Итог урока.

Слайд 25.

- Всё ли мы рассмотрели что хотели?

- Кто уже запомнил формулировку теоремы Пифагора?

- Пригодятся вам эти знания?

Домашнее задание.

Слайд 26.

п. 54

- Кто считает, что полностью разобрался и понял новый материал, решает дома задачи под номерами 484(а, б), 498(а, б).

- У кого возникли вопросы на некоторых этапах нашего урока, решает дома задачи под номерами 483(а, б), 484(а, б).

Почему теорему Пифагора называли «Теоремой Невесты»?

IV. Рефлексивно – оценочный этап.

- Понравился вам урок?

- Давайте заглянем в наши коробочки.

- В какой коробочке листочков больше? (знаю) Так и должно быть. Это правильно

- Теперь добавим новые знания в те, что мы имели.

- Старайтесь с каждого урока выносить новые знания.

- Всё состоит из мелочей! Знание это сила!

- Посчитайте средне – арифметический бал и поставьте себе оценку.

Слайд 27.

- Посмотрите на высказывание Пифагора:

«Из двух человек одинаковой силы сильнее тот, кто прав»

- А кто прав? Как вы думаете?

- Тот, кто мудрее!

- Спасибо за урок!

Литература.

1. Учебник «Геометрия 7-9» Атанасян Л. С, Бутузов В. Ф., Кадомцев СБ., Юдина И. И. Геометрия. 8, Москва, Просвещение, 2008.

2. Гаврилова Н.Ф. Методическое пособие по геометрии: 8 класс. – М.: ВАКО, 2008.

2. http://fcior.edu.ru/card/10969/teorema-pifagora-i3.html

3. http://ru.wikipedia.org
4. http://moypifagor.narod.ru/use.htm

5.  http://moypifagor.narod.ru/literature.htm

Оценочный лист

Ф.И. учащегося
№ п/п	Этап урока	Оценка
1	Определение темы. Составление плана урока.
2	Актуализация опорных знаний.
3	Открытие нового знания. Исследовательская деятельность. Работа в парах.
4	Исторический материал. Работа в группах.
5	Решение задач по готовым чертежам.
6	Разноуровневая самостоятельная работа.
Средне арифметический балл