
Откроем дверь в мир стереометрии, чтобы освоить основной материал по теме:
«Тела вращения»


Слово "цилиндр" происходит от греческого kylindros , что означает "валик", "каток".
Определение . Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
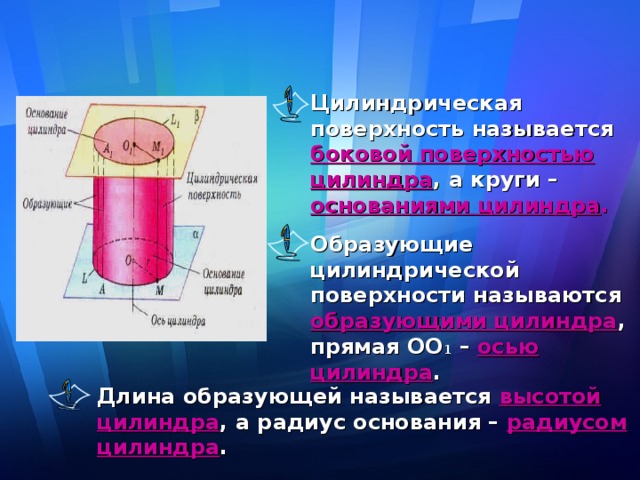
Цилиндрическая поверхность называется боковой поверхностью цилиндра , а круги – основаниями цилиндра .
Образующие цилиндрической поверхности называются образующими цилиндра , прямая ОО 1 – осью цилиндра .
Длина образующей называется высотой цилиндра , а радиус основания – радиусом цилиндра .

Основание цилиндра – круги с центрами О и О 1 , тогда ОО 1 – ось цилиндра и ОО 1 = Н, Н – высота цилиндра, ОО 1 – перпендикуляр к плоскости оснований цилиндра.
Точки А и А 1 , В и В 1 , Х и Х 1 – соответствующие точки.
АА 1 и ВВ 1 – образующие цилиндра, отрезки, соединяющие соответствующие точки на окружностях оснований.
Н

Если образующие перпендикулярны плоскостям оснований, то цилиндр называется прямым . Рассмотрим круговой цилиндр. ОА=О 1 А 1 = R - радиус цилиндра.
Свойства прямого кругового цилиндра:
плоскости оснований цилиндра параллельны, т.е. пл. АОВ II пл. А 1 О 1 В 1 ;
образующие цилиндра параллельны и равны (АА 1 =ВВ 1 , АА II 1 ВВ 1 );
высота цилиндра равна образующей: Н=ОО 1 =АА 1 ;
цилиндр – тело вращения полученное при вращении прямоугольник вокруг одной стороны.

Осевое сечение цилиндра
Сечение цилиндра плоскостью, перпендикулярной к оси.
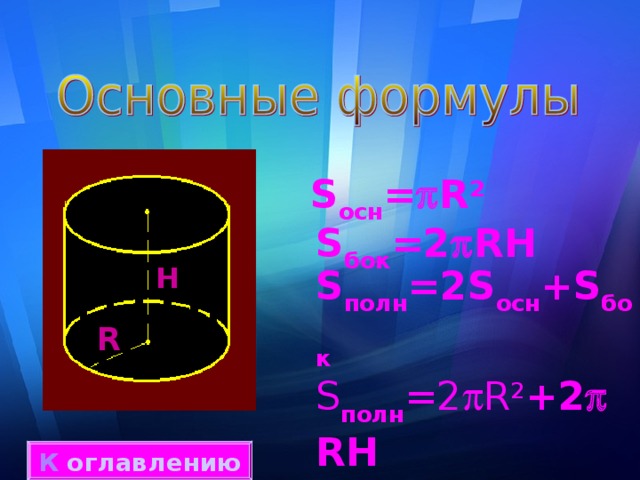
S осн = R 2
S бок =2 RH
S полн =2S осн +S бок
S полн =2 R 2 +2 RH
V=S осн H
V= R 2 H
Н
R
К оглавлению

Латинское слово conus заимствовано из греческого языка (konos - затычка, втулка, сосновая шишка). В XI книге "Начал" даётся следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник снова вернётся в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом . Евклид рассматривает только прямые конусы, лишь Аполлоний различает прямые и косые конусы .

S
S – вершина конуса, О – центр круга, лежащего в основание конуса. Отрезки S А и S В, которые соединяют вершину S с точками окружности основания, называются образующими конуса .
Конус называется прямым , если S О пл. АОВ, ОА=ОВ – радиус конуса. S О – высота конуса .
X
O
B
A

S
Свойства прямого конуса:
Образующие конуса равны SA = SB =,,,(из равенства треугольников SOA , SOB , ,,,по двум катетам);
Так как SO пл. AOB , то S О=Н кон ;
Н
l
О
R
А
Конус – тело вращения, полученное в результате вращения прямоугольного треугольника около его катета как оси.
S ОА вращается около прямой а, содержащей катет S О, тогда S ОА=90 0 и прямая S О – ось конуса. R =АО, Н= S О, А S = l - образующая конуса.
S
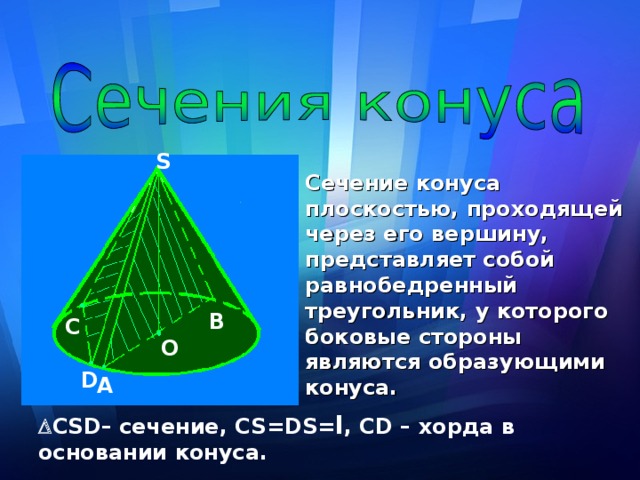
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.
B
C
O
D
A
С SD – сечение, CS = DS= l , CD – хорда в основании конуса.
S
B
C
O
D
A
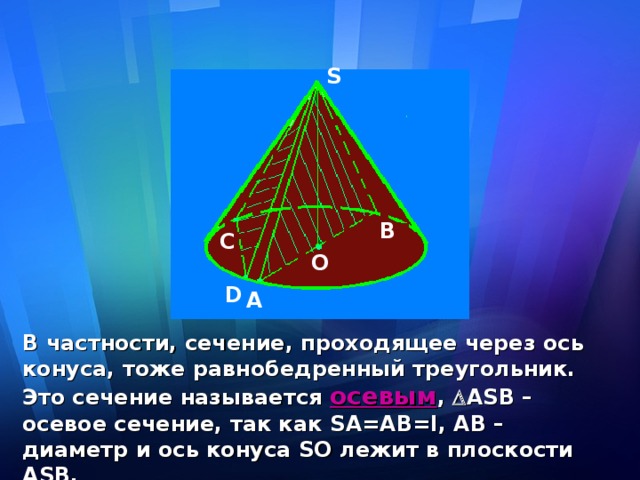
В частности, сечение, проходящее через ось конуса, тоже равнобедренный треугольник. Это сечение называется осевым , А S В – осевое сечение, так как S А=АВ= l , АВ – диаметр и ось конуса S О лежит в плоскости А S В.

S осн = R 2
S бок = RL
S полн =S осн +S бок
S полн = R 2 + RL
V=1/3 . S осн . H
V=1/3 . R 2 H
H
l
R
К оглавлению

Однако оба слова "шар" и "сфера" происходят от одного и того же греческого слова "сфайра" - мяч.
При этом слово "шар" образовалось от перехода согласных сф в ш.

В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Луне, Солнцу, Земле и всем мировым телам.
Развивая взгляды Евдокса, он полагал, что Земля окружена рядом концентрических сфер. Сфера всегда широко применялась в различных областях науки и техники.

Шаром принято называть тело, ограниченное сферой (поверхностью, определяемой как геометрическое место точек пространства, удалённых на данное расстояние от одной точки). В XI книге "Начал" Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом.

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
B
O
A
О – центр шара, ОА=ОВ= R - радиус шара (сферы), АВ – диаметр. А и В – диаметрально противоположные точки.
S c ф = 4 R 2

Х
О 1
О
Теорема . Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость .

Доказательство.
Пусть - секущая плоскость и О – центр шара. Проведем перпендикуляр ОО 1 на плоскость , О 1 , тогда О 1 – основание этого перпендикуляра.
x
o 1
O
Пусть x , где Х– произвольная точка шара, тогда отрезок О 1 Х лежит в плоскости и ОО 1 О 1 Х, т.е. ОО 1 Х=90 0 в ОО 1 Х. По теореме Пифагора ОХ 2 =ОО 1 2 +О 1 Х 2. Так как ОХ R , то О 1 Х= ОХ 2 - ОО 1 2 R 2 - ОО 1 2 , т.е. любая точка Х сечения шара плоскостью находится от точки О 1 на расстоянии, не большем R 2 - ОО 1 2 ,т.е. эта точка принадлежит кругу с центром О 1 и радиусом R 2 - ОО 1 2 .

Верно и обратное утверждение : любая точка Х этого круга принадлежит шару, значит, сечением шара плоскостью является круг с центром в точке О 1 . Теорема доказана.

O
Сечение шара диаметральной плоскостью называется большим кругом.
Плоскость, проходя-щая через центр шара, называется диаметральной плоскостью.
Сечение сферы называется большой окружностью.
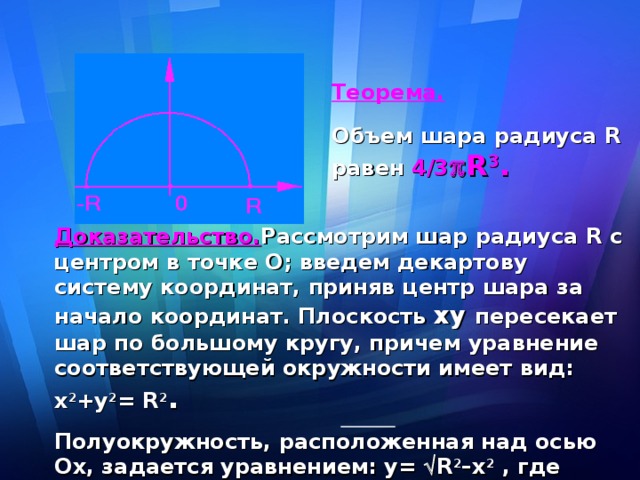
Теорема.
Объем шара радиуса R равен 4/3 R 3 .
Доказательство. Рассмотрим шар радиуса R с центром в точке О; введем декартову систему координат, приняв центр шара за начало координат. Плоскость ху пересекает шар по большому кругу, причем уравнение соответствующей окружности имеет вид: х 2 +у 2 = R 2 .
Полуокружность, расположенная над осью Ох, задается уравнением: у= R 2 –x 2 , где - R х R.

Для нахождения объема шара воспользуемся общей формулой для вычисления объемов тел вращения криволинейной трапеции вокруг оси Ох.
V = ∫ f 2 (x) dx , где f(x) - непрерывная функция, причем f(x) 0 при x a ; b .
Таким образом, объем шара равен:
V = ∫ (R 2 - x 2 ) dx , = (R 2 x – x 3 /3) = ((R 3 – R 3 /3) - (-R 3 + R 3 /3)) =
= 4 /3 R 3 .
Теорема доказана.
Исследование объема шара.xls
b
a
R
R
-R
-R

Пример. Найдите объем шара, радиус которого равен 3см.
Решение. Воспользуемся формулой для нахождения объема шара:
V= 4 /3 . 3 3 = 4 . 9=36 (c м 3 )
Ответ. 36 c м 3 .






