
Галкин Владимир
Работа на конкурс ученических презентаций

Угадай что это?
Треугольник
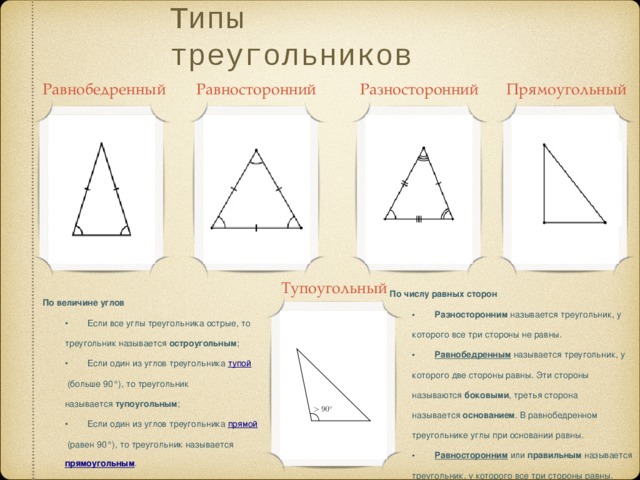
Типы треугольников
Равнобедренный
Прямоугольный
Разносторонний
Равносторонний
Тупоугольный
По числу равных сторон
• Разносторонним называется треугольник, у которого все три стороны не равны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием . В равнобедренном треугольнике углы при основании равны.
• Равносторонним или правильным называется треугольник, у которого все три стороны равны.
По величине углов
• Если все углы треугольника острые, то треугольник называется остроугольным ;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным ;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным .
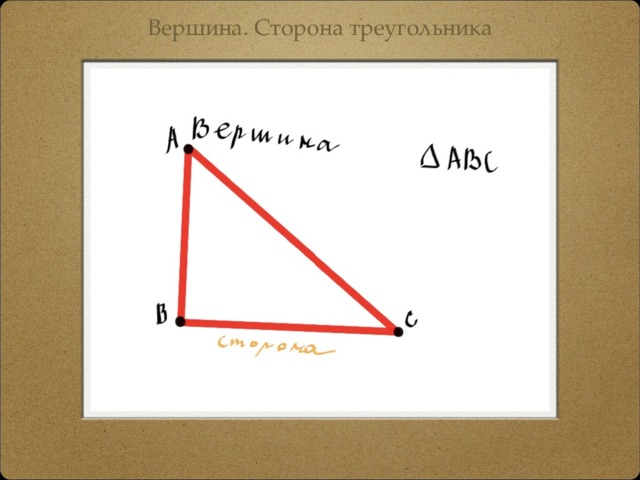
Вершина. Сторона треугольника
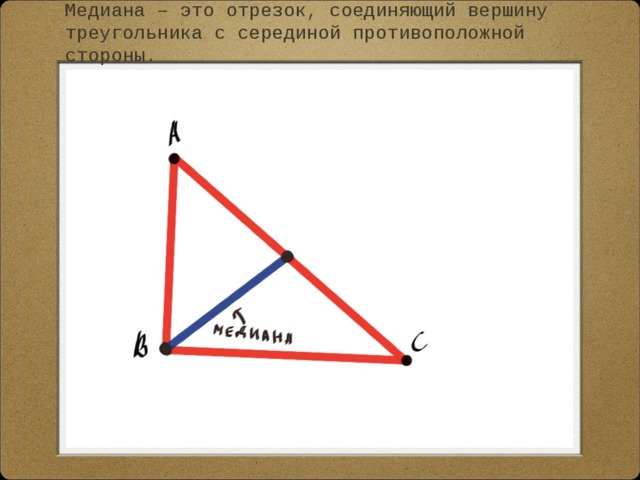
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
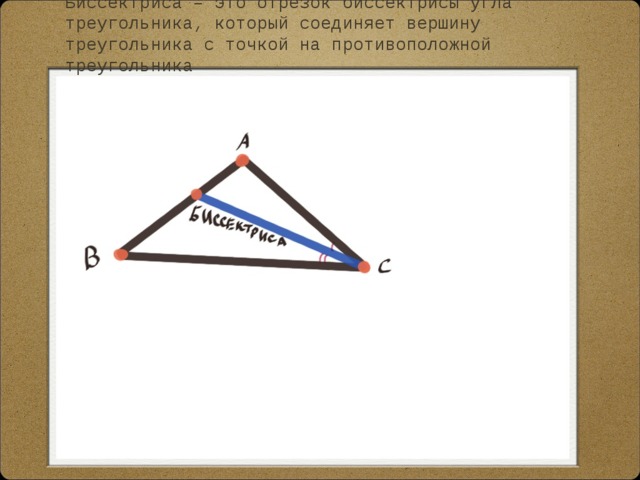
Биссектриса – это отрезок биссектрисы угла треугольника, который соединяет вершину треугольника с точкой на противоположной треугольника
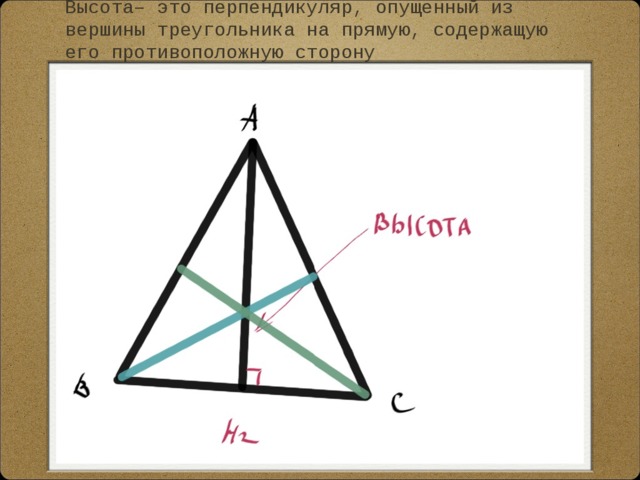
Высота– это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую его противоположную сторону

3 признака равенства треугольника
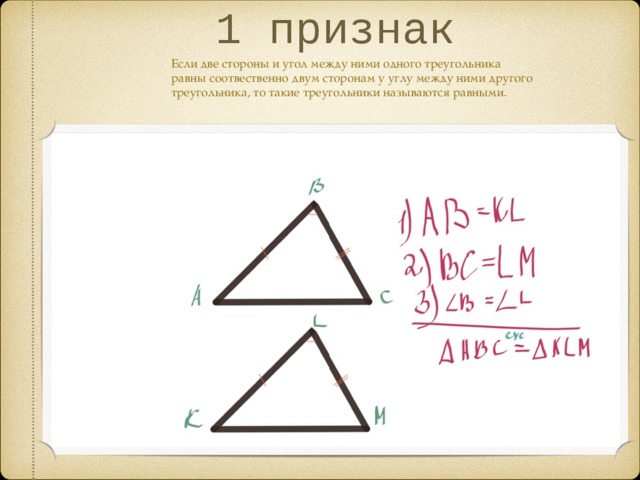
1 признак
Если две стороны и угол между ними одного треугольника равны соотвественно двум сторонам у углу между ними другого треугольника, то такие треугольники называются равными.
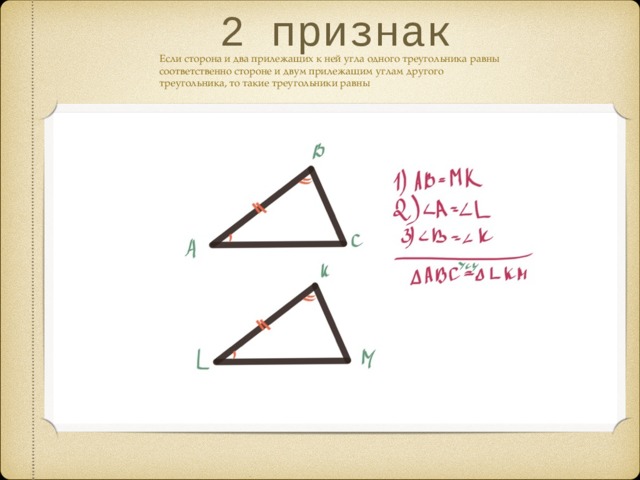
2 признак
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим углам другого треугольника, то такие треугольники равны
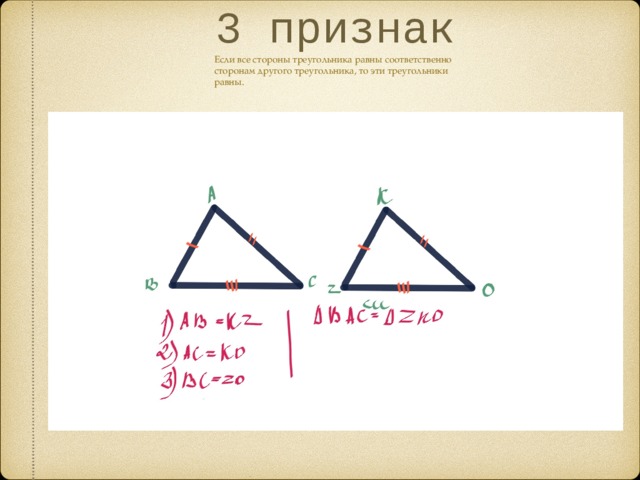
3 признак
Если все стороны треугольника равны соответственно сторонам другого треугольника, то эти треугольники равны.





