
Геометрия
Геометрия - это раздел математики, изучающий пространственные структуры и отношения, а также их обобщения .
Презентацию подготовила Хомякова Александра

История геометрии
- Возникновение геометрии восходит к глубокой древности и было обусловлено практическими потребностями человеческой деятельности (необходимостью измерения земельных участков, измерения объемов различных тел и т. д.).
- Простейшие геометрические сведения и понятия были известны еще в Древнем Египте . В этот период геометрические утверждения формулировались в виде правил, даваемых без доказательств.
- С VII века до н. э. по I век н. э. геометрия как наука бурно развивалась в Древней Греции . В этот период происходило не только накопление различных геометрических сведений, но и отрабатывалась методика доказательств геометрических утверждений, а также делались первые попытки сформулировать основные первичные положения (аксиомы) геометрии , из которых чисто логическими рассуждениями выводится множество различных геометрических утверждений. Уровень развития геометрии в Древней Греции отражен в сочинении Евклида «Начала» .
История геометрии
- В этой книге впервые была сделана попытка дать систематическое построение планиметрии на базе основных неопределяемых геометрических понятий и аксиом (постулатов).
- Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н. И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная.
- «Начала» Евклида оказали огромное влияние на развитие математики. Эта книга на протяжении более чем двух тысяч лет была не только учебником по геометрии, но и служила отправным пунктом для очень многих математических исследований, в результате которых возникли новые самостоятельные разделы математики.
- Систематическое построение геометрии обычно производится по следующему плану:
- I. Перечисляются основные геометрические понятия, которые вводятся без определений.
- II. Дается формулировка аксиом геометрии.
- III. На основе аксиом и основных геометрических понятий формулируются остальные геометрические понятия и теоремы.
- Источник: А.Г. Цыпкин. Справочник по математике, 1983, Москва «Наука».

Что изучает геометрия?
Геометрия изучает форму предметов, определяет их размеры и взаимное расположение.
- Многие предметы имеют прямоугольную форму, другие круглую, третьи - треугольную. Бывают и более сложные формы.
- Если посмотреть более внимательно, то можно заметить, что тот же прямоугольник состоит из четырех отрезков, которые образуют его стороны. Т. е. можно сказать, что большинство фигур состоит из более простых фигур. Все фигуры состоят из точек. Поэтому точку можно считать простейшим элементом.
- При описании фигур важно ни только указать геометрические примитивы, из которых она состоит, но и "отношения" между ними. Например, прямоугольник не просто состоит из четырех отрезков, но они должны быть соединены между собой; углы, образуемые соединенными отрезками, должны быть прямыми; кроме того отрезки должны быть попарно равны, и отрезки с одинаковой длинной располагаться на противоположных сторонах.
- В то же время прямоугольники бывают разными. Один более вытянутый по одной стороне и больше похожий на брусок, у другого ширина и длина не сильно отличаются, и такой прямоугольник похож на квадрат. Ну и понятно, прямоугольники могут различаться по своим размерам. Все это говорит о том, что под термином "прямоугольник" мы понимаем множество фигур, удовлетворяющих определенным требованиям.
- Геометрия - древняя наука. Она возникла около 4-5 тыс. лет назад. Людям с древних времен требовалось измерять земельные участки, расстояния, различные предметы, делать замеры при постройке зданий. Слово «геометрия» в переводе с греческого означает «землемерие».
- Сначала в истории накапливались правила различных геометрических построений. Потом в Древней Греции появились ученые, которые привнесли в геометрию много нового. В частности начали уделять большую роль рассуждениям, на основе которых можно было открыть новые факты и закономерности. Можно сказать, что геометрия как наука сформировалась к началу нашей эры.
- Практическое значение геометрии велико. Кроме того, она учит человека рассуждать, видеть мир форм в их взаимосвязи и взаимодействии.
- Наука геометрия делится на два больших раздела - планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.
- Наука геометрия делится на два больших раздела - планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.

Геометрия в нашей жизни
Многие думают, что математика – сложная, абстрактная, скучная, бесполезная и далекая от реальной жизни наука. Поэтому вы будете удивлены, узнав, что геометрия – важный раздел математики – появилась из-за необходимости решать определенные практические задачи.
- Считается, что ее придумали египтяне , которым нужно было периодически размечать землю , потому что река Нил во время наводнений постоянно стирала границы. В самом деле с точки зрения этимологии слово геометрия означает «измерение земли» .
- Математика настолько практична, что немногое из окружающего нас может без нее функционировать. От банков и магазинов, бирж и страховых компаний до штрих-кодов, прослушивания дисков и разговоров по мобильному телефону – все это и многое другое работает благодаря процессорам и математическим моделям, задача которых – постоянное выполнение математических операций.
- Резкий скачок в развитии технологий и науки произошел в сравнительно сжатые сроки. Физика, медицина, химия, гражданское строительство, архитектура, электроника и освоение космоса, а также многие другие области знаний, которые упрощают нам жизнь, оказались бы нежизнеспособными без изобретенных математикой методов, с помощью которых развивались теоретические модели, на которых основываются их исследования.
- Студенты обычно думают, что математика не имеет практического применения. Однако каждый раз, когда в наших руках оказываются деньги , мы выполняем математические операции. А геометрия, один из основных разделов математики, тесно связана с нашей повседневной жизнью. Наши дома полны объектов, созданных с использованием точных геометрических форм, хотя мы можем этого и не осознавать.
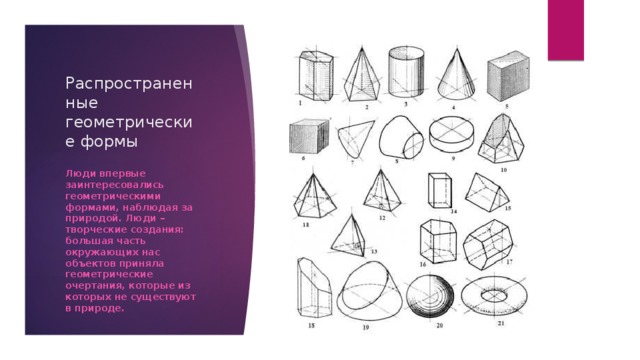
Распространенные геометрические формы
Люди впервые заинтересовались геометрическими формами, наблюдая за природой. Люди – творческие создания: большая часть окружающих нас объектов приняла геометрические очертания, которые из которых не существуют в природе.
- Люди впервые заинтересовались геометрическими формами, наблюдая за природой. Люди – творческие создания: большая часть окружающих нас объектов приняла геометрические очертания, которые из которых не существуют в природе.
- Геометрия присутствует практически во всех сферах нашей жизни: нас окружают круглые, квадратные, прямоугольные, треугольные, сферические, кубические, цилиндрические, конические и другие объекты.
- Обычно мы не задумываемся о том, почему объекты имеют ту или иную форму, а ее выбор далеко не случаен.
- Одна из самых распространенных форм – это окружность и то, что ею ограничено, то есть круг. Вы, наверное, не задумывались, почему трубы – круглые в сечении.
- Одна из причин в том, что окружность – это замкнутая дуга с постоянной шириной. По этой причине, например, люки не проваливаются вниз, что приводило бы к несчастным случаям, а будь они квадратными и прямоугольными, это стало бы неизбежным.
- Еще одно свойство окружности: из всех замкнутых кривых заданной длины круг покрывает наибольшую площадь. Это объясняет тот факт, что природа часто использует круг и его объемный эквивалент – сферу. Природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию.
- Сфера полностью отвечает требованиям, поскольку она обладает максимальным внутренним объемом на единицу поверхности. Это одна из причин, по которой большая часть резервуаров имеет сферическую форму, а консервные банки, термосы и бутылки напоминают цилиндры. Человек попытался совместить минимальную внешнюю поверхность и материалозатраты с максимальным внутренним объемом.
- Небесные тела большой массы, такие как звезды, планеты и спутники тоже сферической формы. Сила притяжения толкает каждый атом к центру тела. Со временем оно приобретает сферическую форму, потому что именно в ней достигается максимальная концентрация массы при минимальной площади внешней поверхности.

Геометрия в искусстве
Использование геометрических форм в искусстве свойственно всем цивилизациям, особенно – исламскому миру.

- Один из самых выдающихся примеров геометрического искусства – это мозаики Альгамбры в испанской Гранаде. Вообще, исламские мозаики – это видоизмененные правильные многоугольники. Еще один из методов создания мозаики – это вращение и наложение правильных многоугольников.
- В 1891 году математик Федоров выдвинул теорию, которую назовут в его честь. Она говорит о том, что такой тип мозаик составляется из 17 основных структур, называемых плоскими кристаллографическими группами.
- Альгамбра – единственный памятник, украшенный 17 основными плоскими декоративными геометрическими рисунками, появившийся до Федорова. Таким образом, средневековые арабские математики эмпирически установили то, что будет доказано лишь через несколько столетий.

Другие практические применения геометрии
Помимо использования в искусстве, геометрия имеет бесчисленное множество практических применений.
- Топография – это геометрия, применяемая для описания местности, на которой нужно что-то построить. Она используется для определений и вычислений расстояний, углов и других параметров, чтобы иметь возможность проводить работы с максимальной точностью.
- Гражданское строительство и архитектура постоянно используют геометрические формы для проектирования разного типа сооружений, таких как мосты, здания, водохранилища, тоннели и автострады.
- Изобретение, которое сегодня используют во многих странах – система глобального позиционирования, которая работает по тому же принципу, что и другие подобные системы — европейская Галилео и российская ГЛОНАСС, и базируется на законах геометрии и тригонометрии. Она используется в таких важных областях, как телефония, телевидение, сети связи, сельское хозяйство, поиск нефти и газа, морской, сухопутный и воздушный транспорт, и даже заменила в наших машинах привычные карты.
- Система GPS использует сеть из 24 спутников, вращающихся вокруг Земли на высоте 20 километров. Навигатор GPS автоматически находит минимум 4 спутника: три – чтобы определить местоположение и четвертый – чтобы компенсировать возможные отклонения. Он получает информацию о времени положении каждого из них. На основании этих сигналов аппарат синхронизирует часы GPS и вычисляет задержку сигнала, т.е. расстояние до спутника. Используя триангуляцию, он определяет точное положение, используя данные об удаленности каждого спутника от точки, в которой проводится измерение.
- Математика развивалась в течение тысячелетий, в основе ее лежала необходимость считать объекты и измерять формы. Это в свою очередь способствовало развитию других наук, которые позволили нам увидеть окружающий мир с совершенно другой стороны.
- Математика – один из мощнейших инструментов, изобретенных человеком для познания окружающего мира. Она позволяет описать эллиптические орбиты планет, измерить площади участков и даже размер телевизионного экрана. Мы не видим субатомный мир и не можем ощутить, что такое миллион лет, но благодаря математике вся реальность — и видимая, и невидимая – стала нам доступна.

А теперь картинки!


Головокружительная
геометрия
Головокружительная
геометрия





