
«ПРИЗМА И ПИРАМИДА»
МБУ ДО ЦДО «Хоста» г. Сочи
Педагог до Жданова Татьяна Владимировна
2020г.

Содержание
- От древности к современности.
- Пирамида.
- Элементы пирамиды.
- Пирамида. Классификация.
- Правильная пирамида.
- Пирамида. Формулы.
- Призма.
- Элементы призмы.
- Призма. Классификация.
- Параллелепипед.
- Параллелепипед. Теоремы.
- Призма. Формулы.
- Задачи.
- Тест.
- Литература

ОТ ДРЕВНОСТИ К СОВРЕМЕННОСТИ
Веками люди смотрели на пирамиды с гробницами фараонов как на памятники ушедшей цивилизации. И только в середине ХХ века ученые обратили внимание на загадочные явления, связанные с ними. Есть гипотеза, что в пирамиде закодирована информация о строении Вселенной, о человеке
и его духовных возможностях. Еще эта геометрическая фигура обладает уникальными лечебными свойствами. Египетские мумии так хорошо сохранились, не только благодаря бальзамированию, но и потому, что находились они внутри пирамиды.

ОТ ДРЕВНОСТИ К СОВРЕМЕННОСТИ
В Древнем Египте гробницы фараонов имели форму пирамид. В III тысячелетии до н.э. египтяне сооружали ступенчатые пирамиды, сложенные из каменных блоков; позже пирамиды приобрели геометрически правильную форму, например пирамида Хеопса, высота которой достигает почти 147 м, и др. Внутри пирамид находились погребальные склепы и коридоры .

ОТ ДРЕВНОСТИ К СОВРЕМЕННОСТИ
При изучении гробниц исследователи обнаружили странный эффект: в пирамидах происходила самоочистка драгоценных камней и металлов, самозаточка режущих инструментов, мумификация продуктов и т.д. Эти эффекты стали широко использовать и в технике, и в магии .
Во многих городах, в том
числе и в Париже, пирамиды стали неотъемлемой частью архитектурных сооружений. При этом мало кто реально понимает, какие последствия могут со временем проявиться .

ОТ ДРЕВНОСТИ К СОВРЕМЕННОСТИ
Многочисленные исследования позволяют утверждать, что на свойства пирамид влияет форма. Материал, из которых они сделаны, никакой роли не играет. В жарких странах, например, для скотоводов-кочевников изготавливают "холодильники" для мяса в виде пирамиды из проволочного, легко собираемого каркаса. Достаточно поставить такой холодильник в тень, и мясо в нем не пропадет в любую жару.
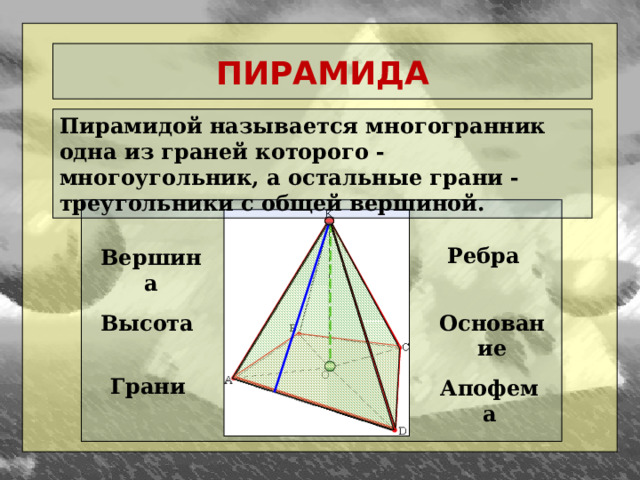
ПИРАМИДА
Пирамидой называется многогранник одна из граней которого - многоугольник, а остальные грани - треугольники с общей вершиной.
Ребра
Вершина
Высота
Основание
Грани
Апофема

ЭЛЕМЕНТЫ ПИРАМИДЫ
Боковые грани пирамиды - треугольники, имеющие общую вершину;
Основание пирамиды - многоугольник, которому не принадлежит вершина пирамиды;
Боковые ребра пирамиды - ребра пирамиды, сходящиеся в ее вершине;
Высота пирамиды - это отрезок перпендикуляра, проведенного через ее вершину к плоскости основания, с концами в вершине и на плоскости основания пирамиды;
Апофема пирамиды - высота боковой грани пирамиды, проведенная из вершины на ребро основания;
Вершина пирамиды - общая вершина боковых граней;
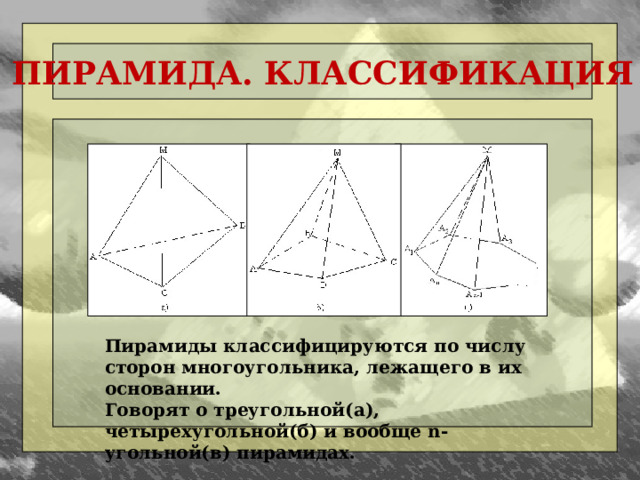
ПИРАМИДА. КЛАССИФИКАЦИЯ
Пирамиды классифицируются по числу сторон многоугольника, лежащего в их основании.
Говорят о треугольной(а), четырехугольной(б) и вообще n-угольной(в) пирамидах.

ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если в её основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).

ПРАВИЛЬНАЯ ПИРАМИДА
Свойства правильной n - угольной пирамиды:
Свойство 1. В правильной n-угольной пирамиде все боковые ребра равны между собой.
Свойство 2. Все боковые грани правильной n-угольной пирамиды суть равные равнобедренные треугольники, поэтому все плоские углы при вершине равны, все плоские углы при основании равны.
Свойство 3. В правильной n-угольной пирамиде
все двугранные углы при основании равны.
Свойство 4. Все плоские при основании равны.
Свойство 5. Апофемы боковых граней
одинаковы по длине.
Свойство 6. В любую правильную пирамиду
можно вписать сферу.

ПИРАМИДА. ФОРМУЛЫ
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
( V=1/3*S ОСН *h )
Площадь боковой грани пирамиды
Площадь боковой поверхности произвольной пирамиды равна сумме площадей её боковых граней или произведению апофемы на половину периметра основания
( S=1/ 2 *P*a )
Площадь полной поверхности пирамиды
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания
( S ПОЛ = S БОК + S ОСН )
Где k – коэффициент подобия, а S 1 и S 2 площади основания малой и большой пирамид
Площадь усеченной пирамиды
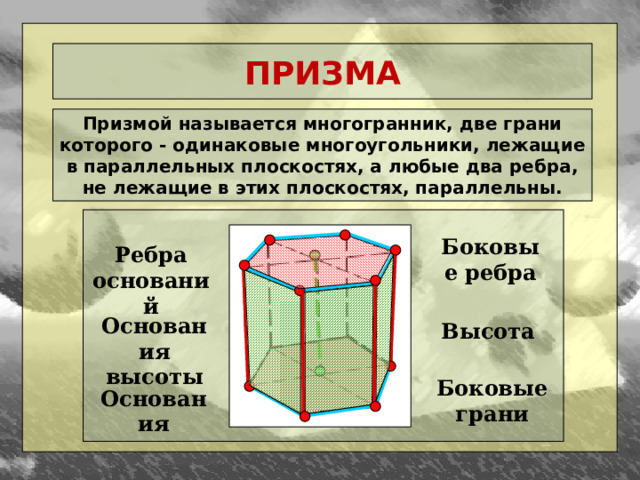
ПРИЗМА
Призмой называется многогранник, две грани которого - одинаковые многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны.
Боковые ребра
Ребра оснований
Основания высоты
Высота
Боковые грани
Основания

ЭЛЕМЕНТЫ ПРИЗМЫ
Основания призмы – два одинаковых многоугольника, лежащие в параллельных плоскостях;
Боковые грани призмы – параллелограммы, являющиеся остальными грани (не основания) призмы;
Боковые ребра призмы - ребра призмы, не лежащие в основание;
Высота призмы – это перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания ;
Диагональная плоскость – это плоскость, проходящая через диагональ основания и боковое ребро призмы.

ПРИЗМА.КЛАССИФИКАЦИЯ
Существуют два вида призм: прямая и наклонная.
Если все боковые ребра призмы перпендикулярны плоскостям ее оснований, то такую призму называют прямой; в противном случае призма называется наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Определение
Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой

ПАРАЛЛЕЛЕПИПЕД
Параллелепипед – это частный случай призмы.
Определение:
Призма, основание которой - параллелограмм, называется параллелепипедом.
Следовательно, параллелепипед - это четырехугольная призма, все грани которой - параллелограммы. Параллелепипеды, имеют все свойства касательные к призме.

ПАРАЛЛЕЛЕПИПЕД. ТЕОРЕМЫ
1. Параллелепипед симметричен относительно середины его диагонали.
2. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадрата трех его измерений.
3. Диагонали параллелепипеда пересекаются в одной точке, совпадающей с серединой каждой из них.
4. Диагонали прямоугольного параллелепипеда равны между собой. Квадрат диагонали равен сумме квадратов трёх измерений.
5. Параллелепипеды с одинаковыми высотами и равновеликими основаниями равновелики.
7. В равновеликих параллелепипедах площади оснований обратно пропорциональны высотам.

ПРИЗМА.ФОРМУЛЫ
Объем призмы - произведение площади основания и высоту
( V=S ОСН *h )
Площадь боковой поверхности призмы - произведение периметра ее перпендикулярного сечения и длины бокового ребра
(S БОК = Р ОСН * l )
Площадь боковой поверхности прямой призмы - произведение периметра ее основания и высоты (S БОК = Р ОСН * h )
Площадь поверхности призмы (S ПР ) равна сумме площадей ее боковых граней (площади боковой поверхности S БОК ) и площадей двух оснований (2S ОСН ) - равных многоугольников: ( S ПР =S БОК +2S ОСН )

ЗАДАЧИ:
Основание пирамиды - равнобедренный треугольник с основанием 6 и высотой 9. Каждое боковое ребро равно 13.
Найдите объём пирамиды.

ЗАДАЧИ
Решение
Пусть ABCD - треугольная пирамида с основанием ABC , DA = DB = DC = 13 , BC = 6 , AK = 9 ( K - середина BC ). Из прямоугольного треугольника AKC находим, что
Поскольку боковые рёбра пирамиды равны, её высота проходит через центр O окружности, описанной около основания. Пусть R - радиус этой окружности. Тогда
Из прямоугольного треугольника AOD находим, что

ЗАДАЧИ
Решение(продолжение)
Следовательно ,
V ABCD = 1/3 S ABC * DO = 1/3 * 1/2BC * AK * DO =
= 1/3 * 1/2 * 6 * 9 * 12 = 108 .
Ответ: 108 .

ЗАДАЧИ
Найдите объём правильной четырёхугольной призмы, если её диагональ образует с плоскостью боковой грани угол 30 o , а сторона основания равна a .

ЗАДАЧИ
Решение
Пусть ABCDA 1 B 1 C 1 D 1 - правильная призма с основанием ABCD и боковыми рёбрами AA 1 , BB 1 , CC 1 и DD 1 , причём AB = a . Поскольку прямая AD перпендикулярна плоскости грани CDD 1 C 1 , DC 1 - ортогональная проекция диагонали AC 1 на эту плоскость, а AC 1 D - угол прямой AC 1 с плоскостью грани CDD 1 C 1 . По условию задачи AC 1 D = 30 o . Из прямоугольных треугольников AC 1 D и DCC 1 находим, что
Ответ :
a 3 √ 2 .
а т.к. CC 1 - высота призмы, то
V ABCDA 1 B 1 C 1 D 1 = S ABCD * CC 1 = a 2 * a√2 = a 3 √ 2 .

ТЕСТ
1. Тетраэдр – это:
а) правильная треугольная призма
б) правильная четырехугольная пирамида
в) треугольная пирамида
2. Апофема – это:
а) высота боковой грани пирамиды
б) высота пирамиды
в) высота призмы
3. Формула площади боковой поверхности призмы:
а) S бок = ½* P*h
б) S бок = Р осн * l
в) S бок = 1/3S*h

Литература
1. Глейзер Г.Д. Геометрия. Методическое пособие для 10-11 классов. -М., Бином, 2012.
2. Атанасян Л. С. Геометрия. Учебное пособие для 7-11 классов. - М., Просвещение, 2019.
3. В помощь учителю. Задания на готовых чертежах по стереометрии 10-11 класс. – Волгоград, Учитель, 2020.
4. Справочник школьника. Универсальное учебное пособие для 5-11 классов. - СПб., ИД «Весь», 2003.
5. J . E. Brown . О древних пирамидах. Энциклопедия. - М., ИД «Красный», 2001.





