

Планиметрия
Стереометрия
Изучает свойства геометрических фигур на плоскости
Изучает свойства фигур в пространстве
В переводе с греческого слово «геометрия» означает «землемерие»
«гео» – по-гречески земля, «метрео» – мерить
Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео» – мерить
Л.С. Атанасян. Геометрия 10-11. п. 1.

Планиметрия
Стереометрия
Основные фигуры: точка, прямая, плоскость
Основные фигуры: точка, прямая
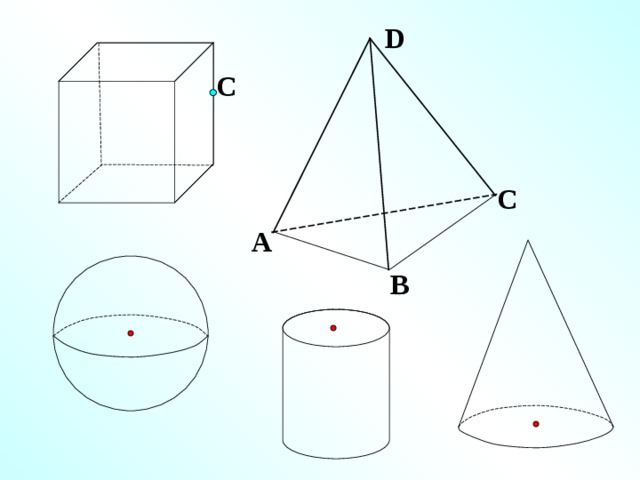
Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности.
Например, многогранники. Куб, параллелепипед, призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр, конус.
Другие фигуры: отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n- угольники, круг, окружность, дуга и др.
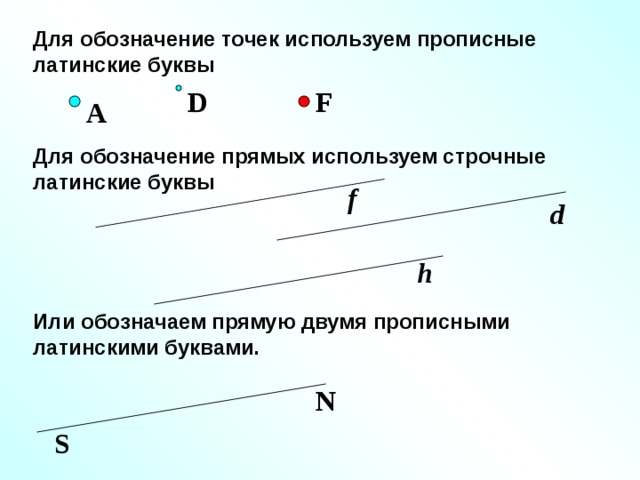
Для обозначение точек используем прописные латинские буквы
D
F
A
Для обозначение прямых используем строчные латинские буквы
f
d
h
Или обозначаем прямую двумя прописными латинскими буквами.
N
S
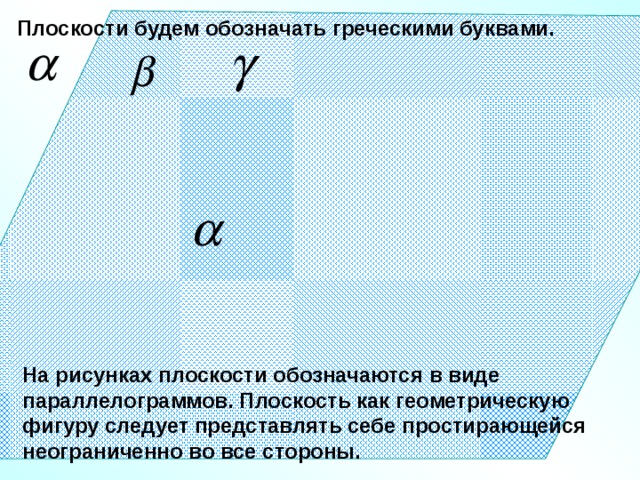
Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде параллелограммов. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
D
C
C
A
B
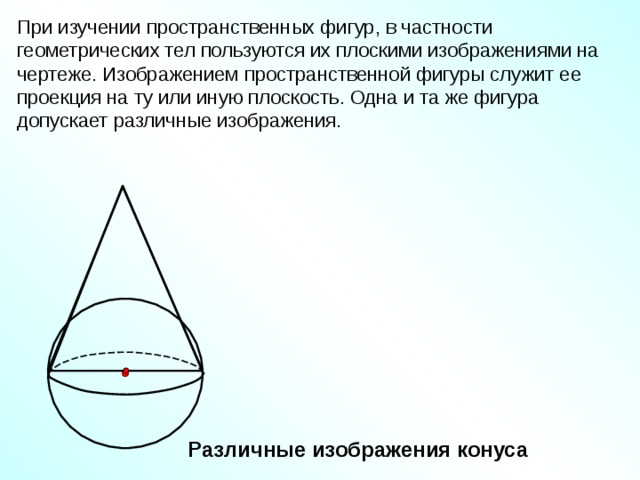
При изучении пространственных фигур, в частности геометрических тел пользуются их плоскими изображениями на чертеже. Изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения.
Различные изображения конуса

Стереометрия широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
При
проектировании
этой машины важно было получить такую форму, чтобы при движении сопротивление воздуха было минимально.

Оперный театр в Сиднее
Датский архитектор Йорн Утцон был вдохновлён видом парусов.

Эйфелева башня
Париж, Марсово поле
Инженер Гюстав Эйфель нашел необычную форму для своего проекта.
Эйфелева башня весьма устройчива: сильный ветер отклоняет ее вершину всего лишь на 10-12 см. В жару от неравномерного нагревания солнечными лучами она может отклониться на 18 см.

Обратите внимание, что при конструировании используется «жесткая» фигура планиметрии – треугольник.
18000 железных деталей скрепляются 2500000 заклёпками
7
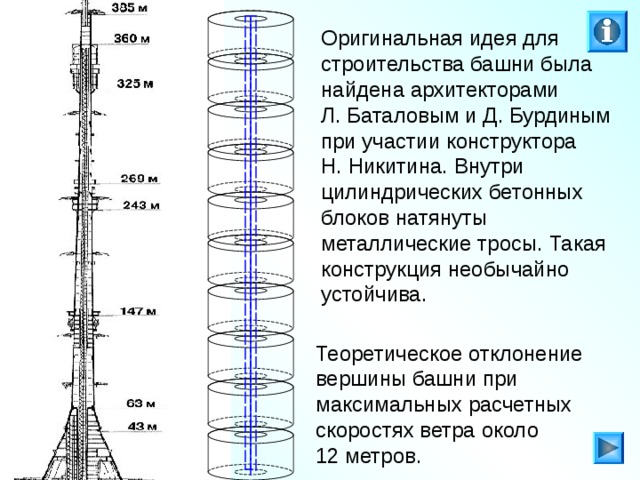
Оригинальная идея для строительства башни была найдена архитекторами
Л. Баталовым и Д. Бурдиным при участии конструктора
Н. Никитина. Внутри цилиндрических бетонных блоков натянуты металлические тросы. Такая конструкция необычайно устойчива.
Теоретическое отклонение
вершины башни при
максимальных расчетных
скоростях ветра около
12 метров.
12
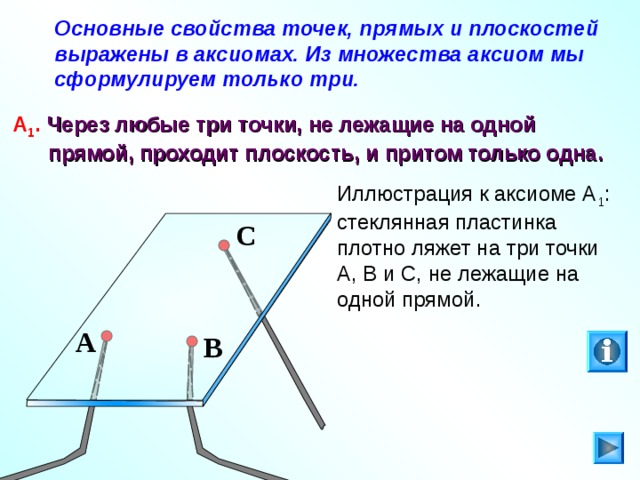
Основные свойства точек, прямых и плоскостей выражены в аксиомах. Из множества аксиом мы сформулируем только три.
А 1 . Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
Иллюстрация к аксиоме А 1 : стеклянная пластинка плотно ляжет на три точки А, В и С, не лежащие на одной прямой.
C
На кнопку « i » можно нажать несколько раз.
A
B
13

Иллюстрации к аксиоме А 1 из жизни.
Для видеокамеры, фотосъемки и для других приборов часто используют штатив – треногу. Три ножки штатива устойчиво расположатся на любом полу в помещениях, на асфальте или прямо на газоне на улице, на песке на пляже или в траве в лесу. Три ножки штатива всегда найдут плоскость.
Табурет с тремя ножками всегда идеально встанет на пол и не будет качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине. Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.
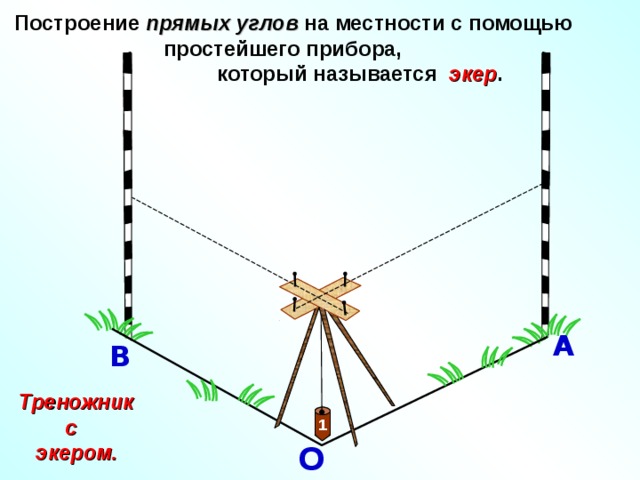
Построение прямых углов на местности с помощью
простейшего прибора,
который называется экер .
Геометрия 7-9. Л. С. Атанасян. Перпендикулярные прямые. Этот слайд вам еще пригодится при изучении темы «Перпендикулярность прямых и плоскостей». Отвес перпендикулярен плоскости земли.
А
В
Треножник
с
экером.
1
О
15
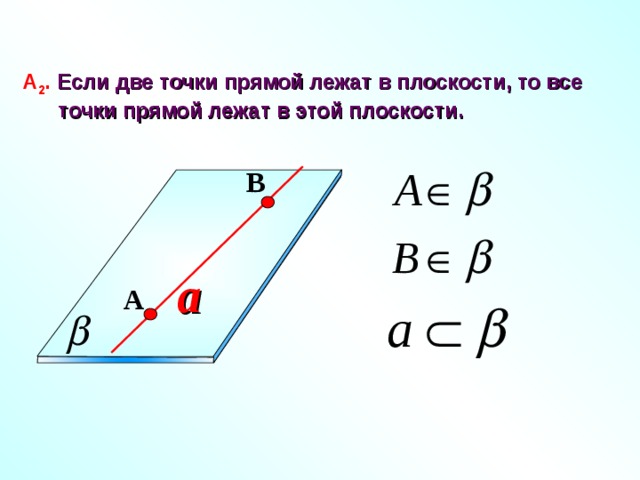
А 2 . Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
B
a
A
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
16
I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
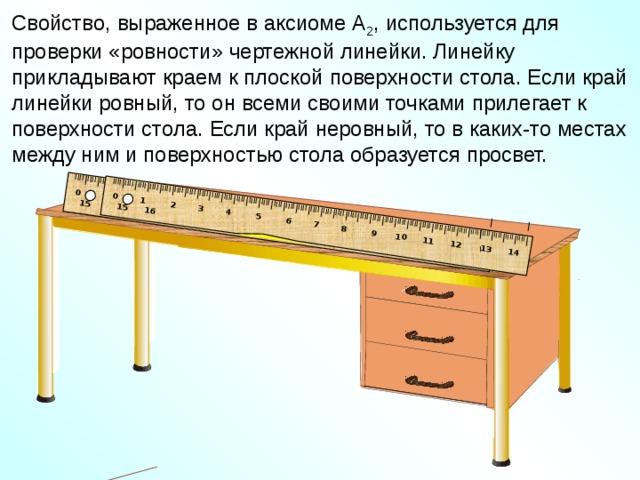
Свойство, выраженное в аксиоме А 2 , используется для проверки «ровности» чертежной линейки. Линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
17
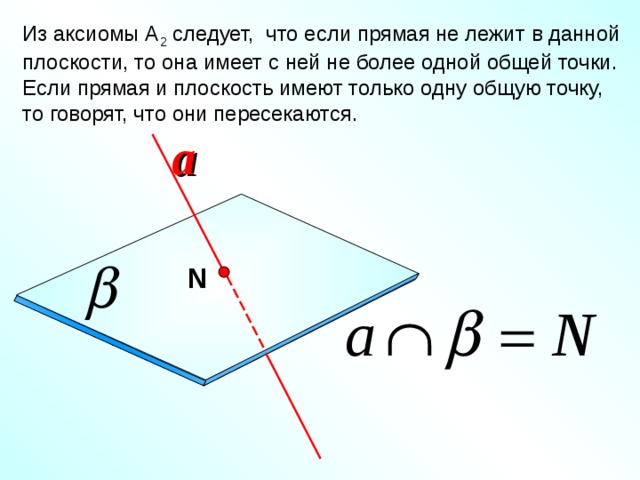
Из аксиомы А 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
a
N
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
18
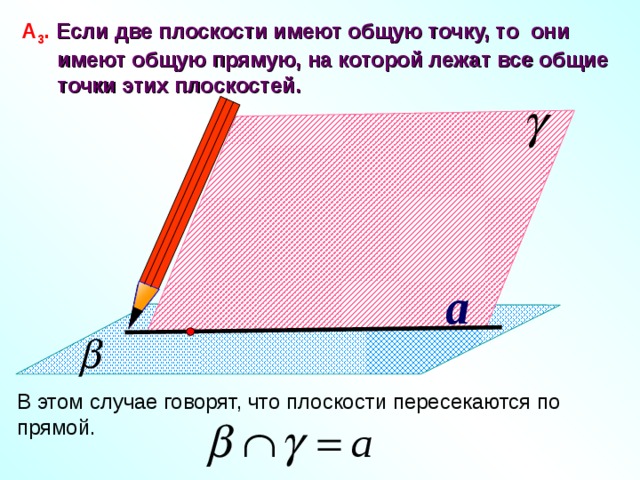
А 3 . Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.
В этом случае говорят, что плоскости пересекаются по прямой.
19
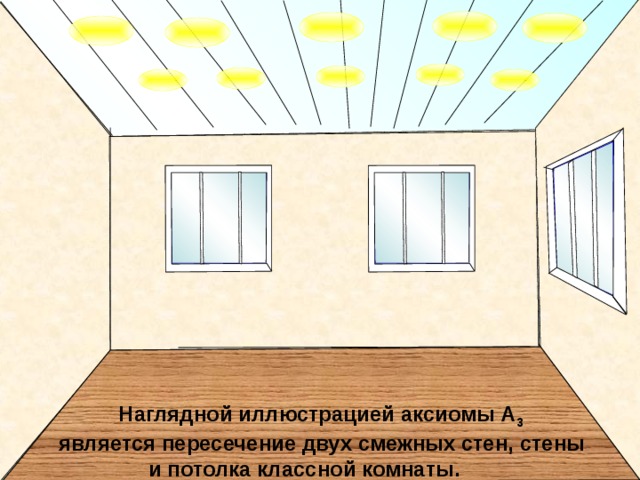
Наглядной иллюстрацией аксиомы А 3
является пересечение двух смежных стен, стены
и потолка классной комнаты.
20
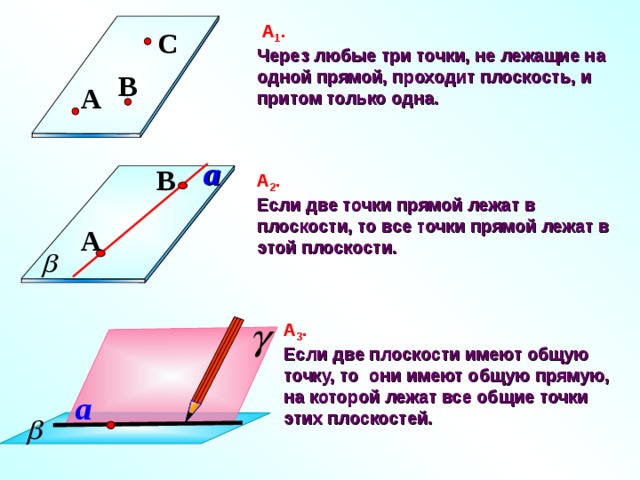
А 1 .
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
C
B
A
a
B
А 2 .
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
A
А 3 .
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
a
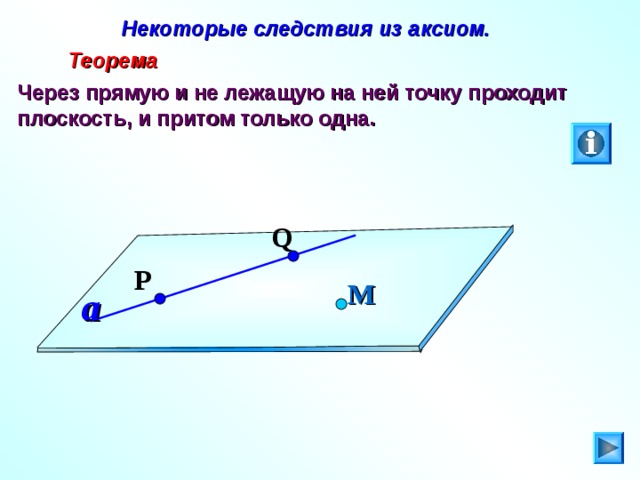
Некоторые следствия из аксиом.
Теорема
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Q
P
М
a
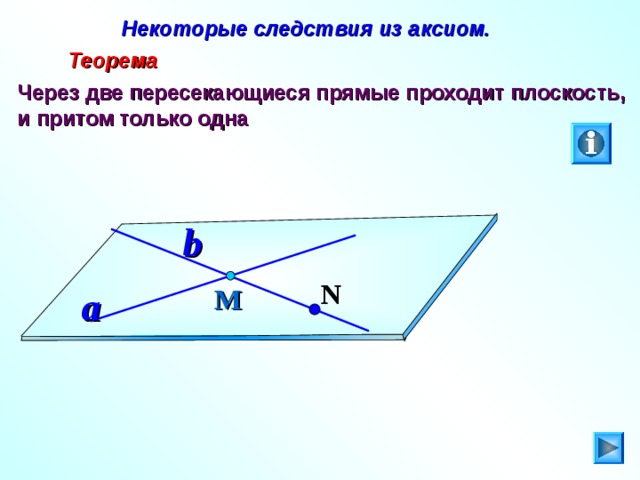
Некоторые следствия из аксиом.
Теорема
Через две пересекающиеся прямые проходит плоскость, и притом только одна
b
N
М
a
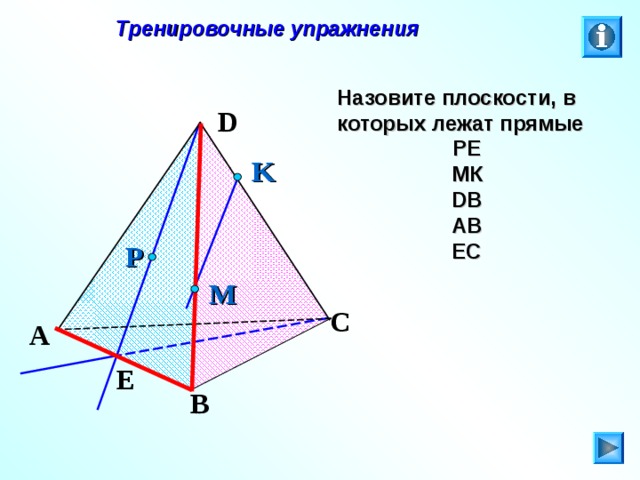
Тренировочные упражнения
Назовите плоскости, в которых лежат прямые
РЕ
МК
DB
AB
EC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8. На кнопку « i » нажмите несколько раз.
A
E
B
24
Тренировочные упражнения
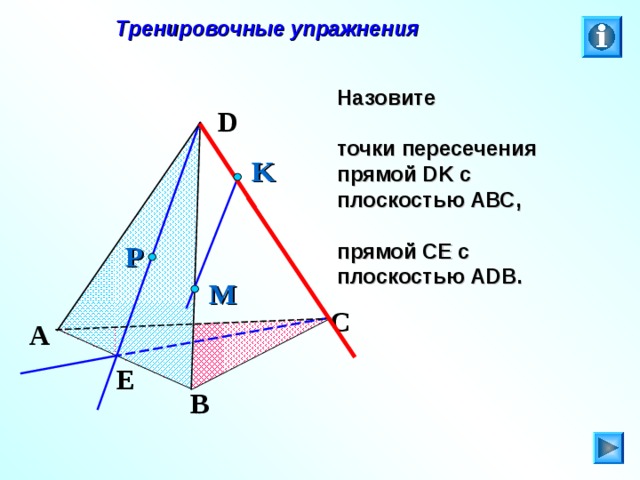
Назовите
точки пересечения прямой DK с плоскостью АВС,
прямой СЕ с плоскостью А DB .
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
25
Тренировочные упражнения
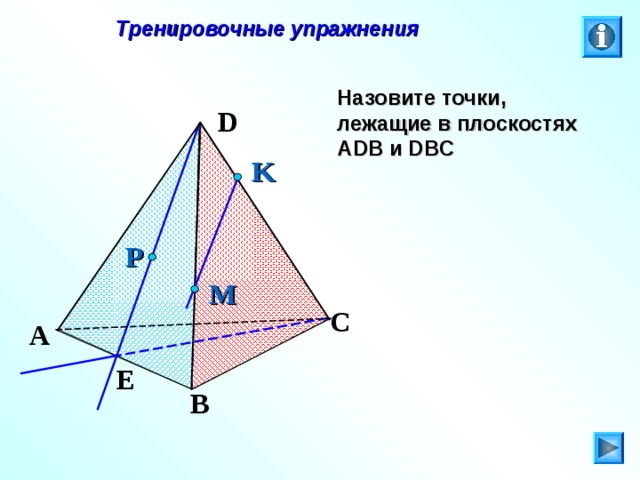
Назовите точки, лежащие в плоскостях А DB и DBC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
26
Тренировочные упражнения
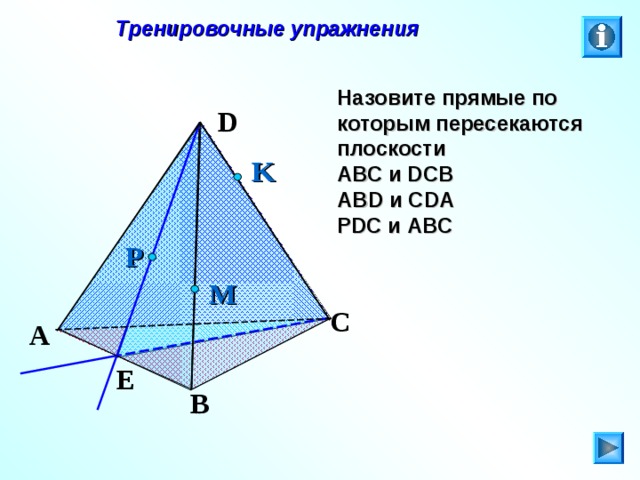
Назовите прямые по которым пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC
D
K
P
M
C
Л.С. Атанасян. Геометрия 10-11. № 8.
A
E
B
27
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
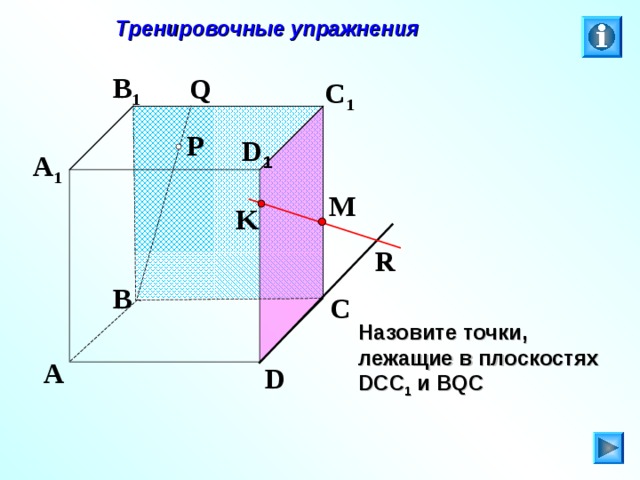
Назовите точки, лежащие в плоскостях DCC 1 и BQC
A
D
27
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
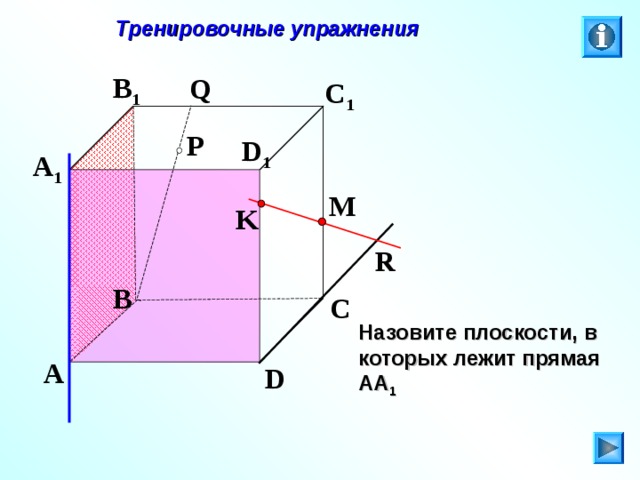
Назовите плоскости, в которых лежит прямая АА 1
A
D
27
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
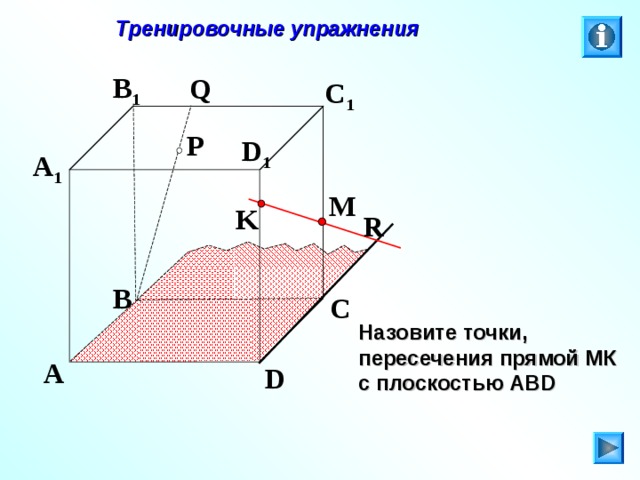
Назовите точки, пересечения прямой МК с плоскостью АВ D
A
D
27
Тренировочные упражнения
B 1
Q
C 1
P
A 1
D 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
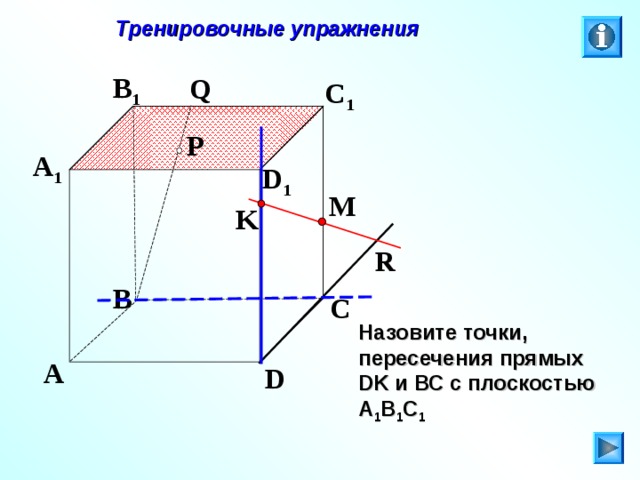
Назовите точки, пересечения прямых DK и ВС с плоскостью А 1 В 1 С 1
A
D
27
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
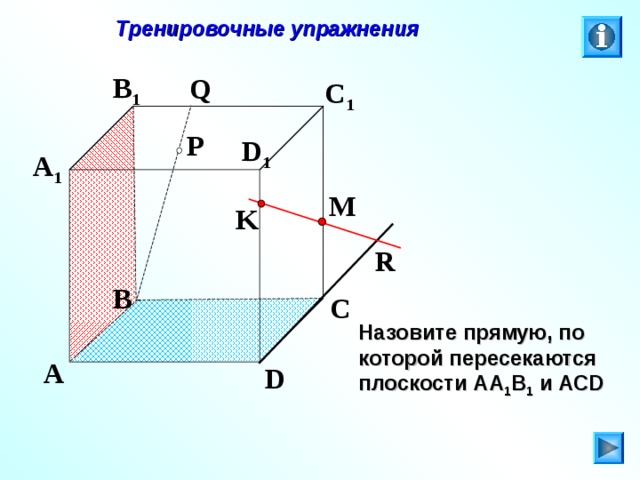
Назовите прямую, по которой пересекаются плоскости АА 1 В 1 и АС D
A
D
27
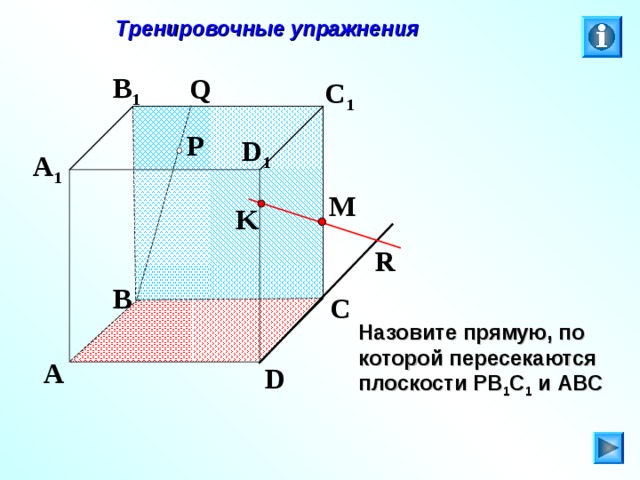
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
Назовите прямую, по которой пересекаются плоскости P В 1 C 1 и ABC
A
D
27
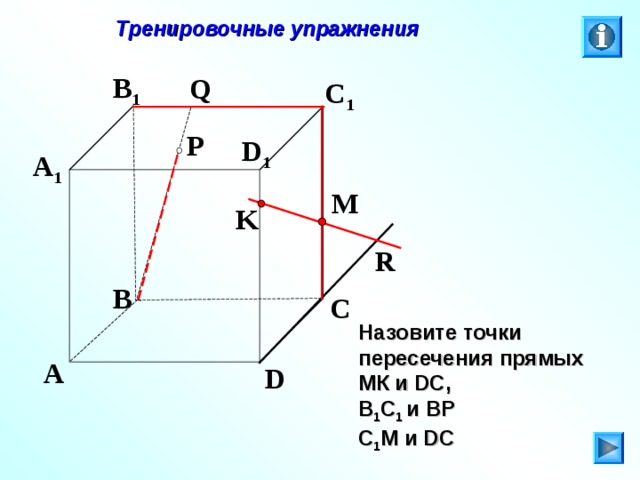
Тренировочные упражнения
B 1
Q
C 1
P
D 1
A 1
M
K
R
B
C
Л.С. Атанасян. Геометрия 10-11. № 9.
Назовите точки пересечения прямых МК и DC ,
В 1 С 1 и ВР
С 1 М и DC
A
D
27





