
Пустые слайды предназначены для того, чтобы не отвлекать учеников от другого вида работы
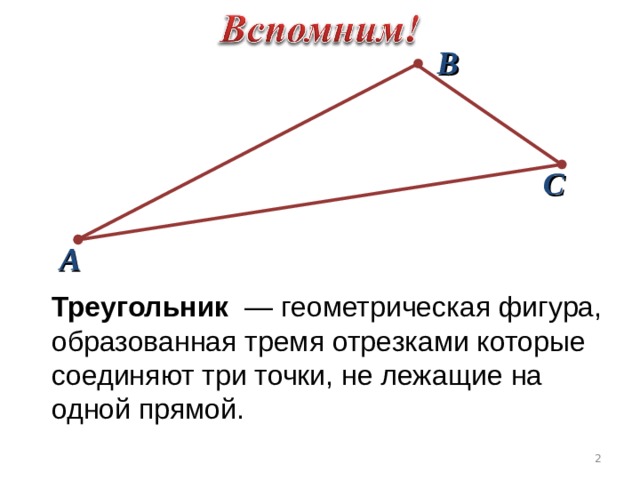
В
С
А
Треугольник — геометрическая фигура, образованная тремя отрезками которые соединяют три точки, не лежащие на одной прямой.
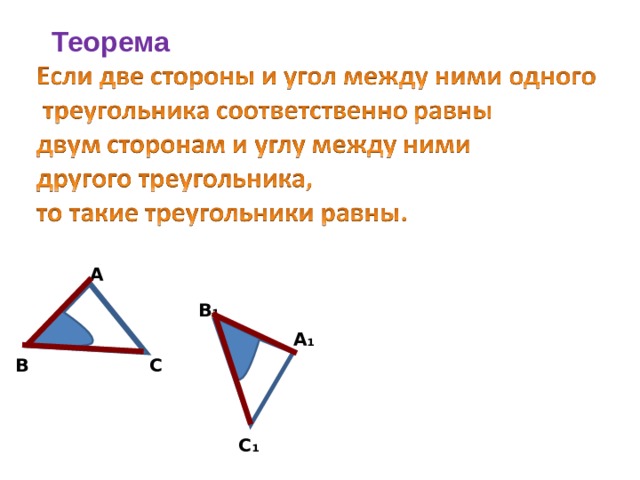
Теорема
А
В₁
А₁
С
В
С₁
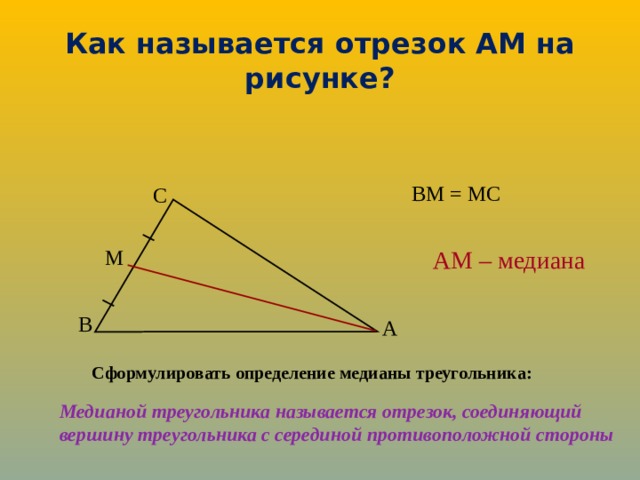
Как называется отрезок АМ на рисунке?
ВМ = МС
С
АМ – медиана
М
В
А
Сформулировать определение медианы треугольника:
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны
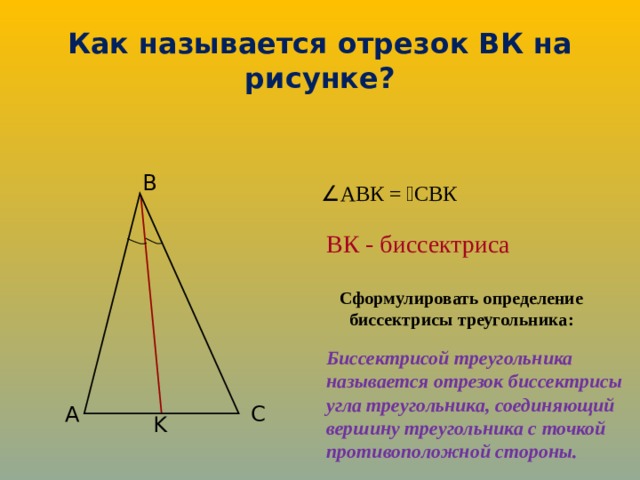
Как называется отрезок ВК на рисунке?
B
АВК = СВК
ВК - биссектриса
Сформулировать определение биссектрисы треугольника:
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
A
C
K
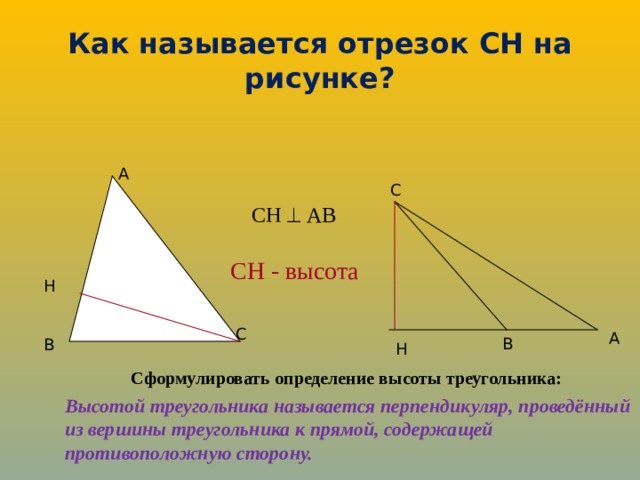
Как называется отрезок СН на рисунке?
A
C
СН АВ
СН - высота
H
C
A
B
B
H
Сформулировать определение высоты треугольника:
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

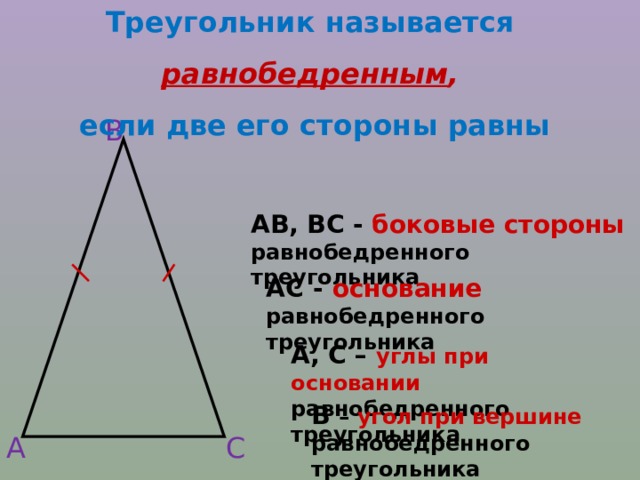
Треугольник называется
равнобедренным ,
если две его стороны равны
В
АВ, ВС - боковые стороны равнобедренного треугольника
АС - основание равнобедренного треугольника
А, С – углы при основании равнобедренного треугольника
В – угол при вершине равнобедренного треугольника
А
С
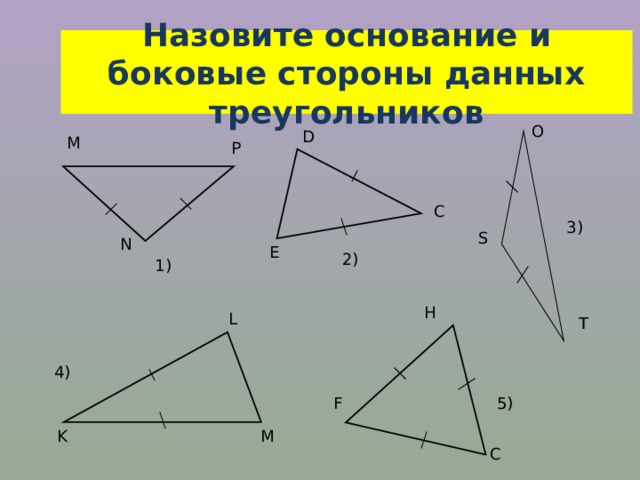
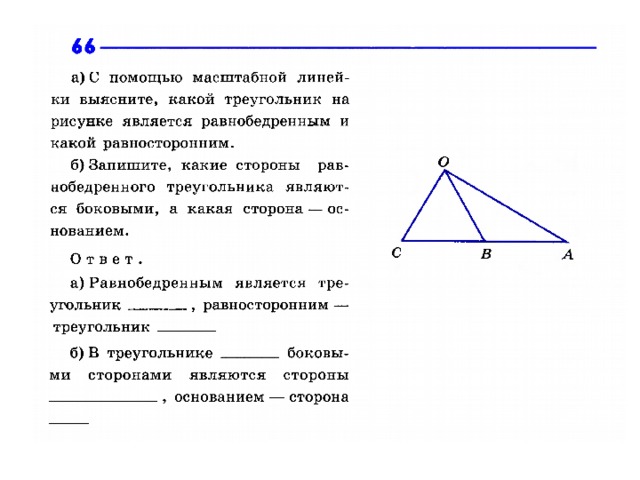
Назовите основание и боковые стороны данных треугольников
O
D
М
Р
C
3 )
S
N
E
2)
1 )
H
L
T
4 )
5)
F
K
M
C
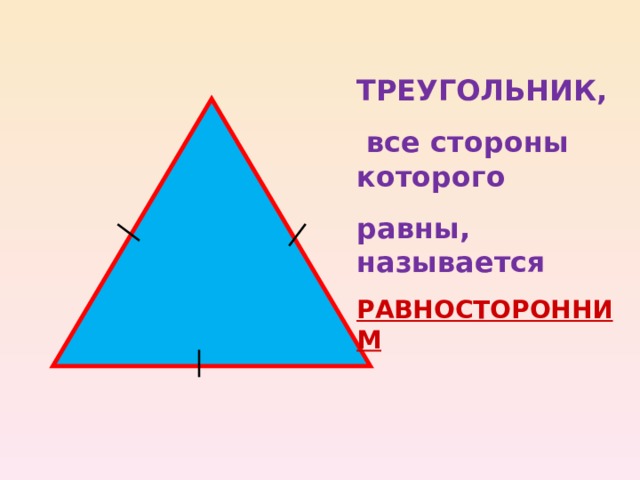
ТРЕУГОЛЬНИК,
все стороны которого
равны, называется
РАВНОСТОРОННИМ

Теорема 1
В равнобедренном треугольнике углы
при основании равны
B
Дано: АВС – равнобедренный, АС – основание
Доказать: А = С
A
C

Доказательство:
- Проведём В D – биссектрису АВС
2. Рассмотрим АВ D и СВ D
АВ=ВС, В D -общая, АВ D = СВ D , значит АВ D = СВ D ( по двум сторонам и углу между ними)
3. В равных треугольниках против равных сторон лежат равные углы А= С
Теорема доказана
B
A
C
D

Теорема 2
В равнобедренном треугольнике биссектриса, проведённая к основанию,
является медианой и высотой
B
Дано: АВС –равнобедренный,
АС – основание,
В D – биссектриса.
Доказать: 1. В D – медиана
2. В D – высота
A
C
D
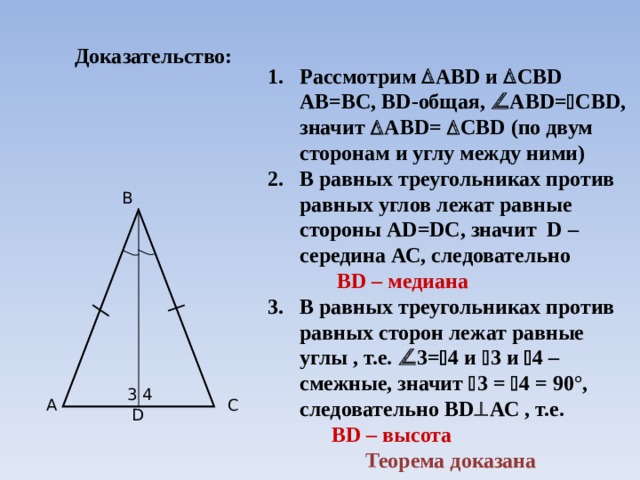
Доказательство:
- Рассмотрим АВ D и СВ D
АВ=ВС, В D -общая, АВ D = СВ D , значит АВ D = СВ D ( по двум сторонам и углу между ними)
2. В равных треугольниках против равных углов лежат равные стороны А D=DC , значит D – середина АС, следовательно
В D – медиана
3. В равных треугольниках против равных сторон лежат равные углы , т.е. 3= 4 и 3 и 4 – смежные, значит 3 = 4 = 90°, следовательно В D АС , т.е.
В D – высота
Теорема доказана
B
3
4
A
C
D
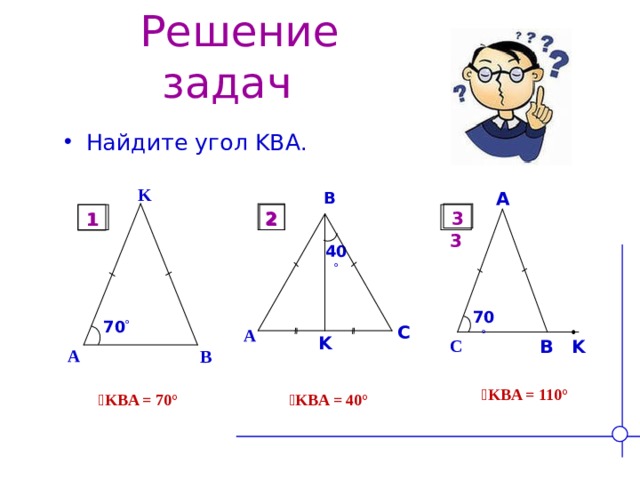
Решение задач
- Найдите угол KBA .
K
B
A
3
2
1
3
2
1
40
70
70
C
A
K
C
B
K
A
B
ے KBA = 110°
ے KBA = 40°
ے KBA = 70°


В классе:
- № 108
- № 112
- № 116
- № 67, № 69(в раб. тет.)
1 вариант
2 вариант
Дано: ∆АВС - равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти : S∆ АВС
Дано: ∆ MNP - равнобедренный,
N К – биссектриса
N К = 5 см,
MP = 12 см
Найти : S∆MNP
B
N
М
A
K
P
C
M
Дано: ∆АВС - равнобедренный,
Найти :
Дано : ∆ MNP - равнобедренный,
Найти :
N
B
40°
70°
A
P
C
М
1 вариант
2 вариант
Дано: ∆АВС - равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти : S∆ АВС
Дано: ∆ MNP - равнобедренный,
N К – биссектриса
N К = 5 см,
MP = 12 см
Найти : S∆MNP
B
N
Решение:
Решение:
NK- высота,
S =
ВМ - высота,
S =
NK·MP
ВМ·АС
S = 63
S = 30
М
K
P
M
C
A
Дано: ∆АВС - равнобедренный,
Найти :
Дано : ∆ MNP - равнобедренный,
Найти :
N
B
40°
Решение
Решение
70°
A
P
М
C
П. 18 теоремы,
№ 109, №117 – из учебника
Р.т. №8
Дополнительная задача:
Доказать, что в равнобедренном
треугольнике медиана,
проведённая к основанию
является биссектрисой и высотой.





