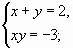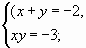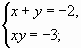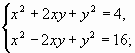Открытый урок "Системы уравнений с двумя неизвестными"

Муниципальное образовательное учреждение

средняя общеобразовательная школа района имени Лазо рабочего поселка Мухен

Открытый урок на тему: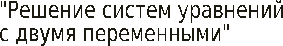

в 9 классе

Кушнарь Лариса Александровна

учитель математики первой квалификационной

категории

2017– 2018 учебный год

Девиз: «Три пути ведут к знанию:

путь размышления – это путь самый благородный,

путь подражания – это путь самый легкий

и путь опыта – это путь самый горький».

Конфуций.

Тип урока: урок обобщения и систематизации знаний.

Цель урока:

Формирование ключевых компетентностей:

а) усвоение знаний в их системе, умение самостоятельно применять полученные ЗУН, осуществлять их перенос в новые условия;

б) развитие умений рассчитывать свои силы и оценивать свои возможности;

в) воспитание умения контролировать внимание на всех этапах урока.

Задачи урока:

• Выявить уровень усвоения полученных знаний;

• Создать условия для самооценки своих возможностей и выбора цели в деятельности;

• Развивать навыки индивидуальной и самостоятельной работы;

• Побуждать к само-, взаимоконтролю;

• Вызывать потребность в обосновании своих высказываний.

Психологическая установка

• Продолжаем отрабатывать навыки решения систем уравнений;

• Формируем математическую интуицию;

• На уроке можем ошибаться, сомневаться, консультироваться.

• Каждый учащийся сам себе дает установку

Содержание урока

1.Разминка. Проверка домашнего задания;

2.Решение систем уравнений с двумя переменными алгебраическими способами;

3. .Решение систем уравнений с двумя переменными графическим способом;

4.Исследование систем уравнений и новые открытия.

5. Итоги урока.

I. Оборудование: доска, набор заданий, карточки с заданием тестов, индивидуальные оценочные листы, презентация урока, мультимедийная установка.

Работа учащихся состоит из этапов. Результаты каждого этапа ученики заносят в индивидуальные оценочные листы и показывают cвое эмоциональное состояние.

ОЦЕНКА МОЕЙ РАБОТЫ НА УРОКЕ.

Фамилия ученика…………………………………..

Этап	Вид работы	Оценка	Эмоциональное состояние
1	Разминка. Проверка домашнего задания.
2	Решение систем уравнений алгебраическими способами
3	Графическое решение систем двух уравнений с двумя переменными.
4	Исследование систем уравнений
5	Общая оценка.

Ход урока

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

• Учитель сообщает учащимся тему и цель урока.

• Рассказывает о том, как будет построен урок.

• Знакомит с требованиями ведения оценочного листа.

Этап I Начало урока посвящается проверке знаний.

Решение систем, содержащих два уравнения с двумя переменными второй степени весьма трудная задача, но в некоторых случаях системы могут быть решены с помощью простых и изящных приемов. Открыть некоторые из них – это цель домашней работы в группах.

4 группам дано задание решить систему уравнений: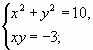

Ученик 1 групппы показывает решение системы уравнений:

- графическим способом.

Решение:

В одной системе координат построим графики уравнений: и ху= -3.

-графиком этого уравнения является окружность с центром в точке (0;0) и радиусом .

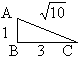
В треугольнике АВС,АВС =90°, АВ=1, ВС=3, АС=.

Длину отрезка АС= возьмем за радиус окружности .

ху=3; у=; - графиком этого уравнения является гипербола, ветви которой расположены во II и IV координатных углах.

х	-6	-3	-1	-0.5	0.5	1	3	6
у	0.5	1	3	6	-6	-3	-1	-0.5

 

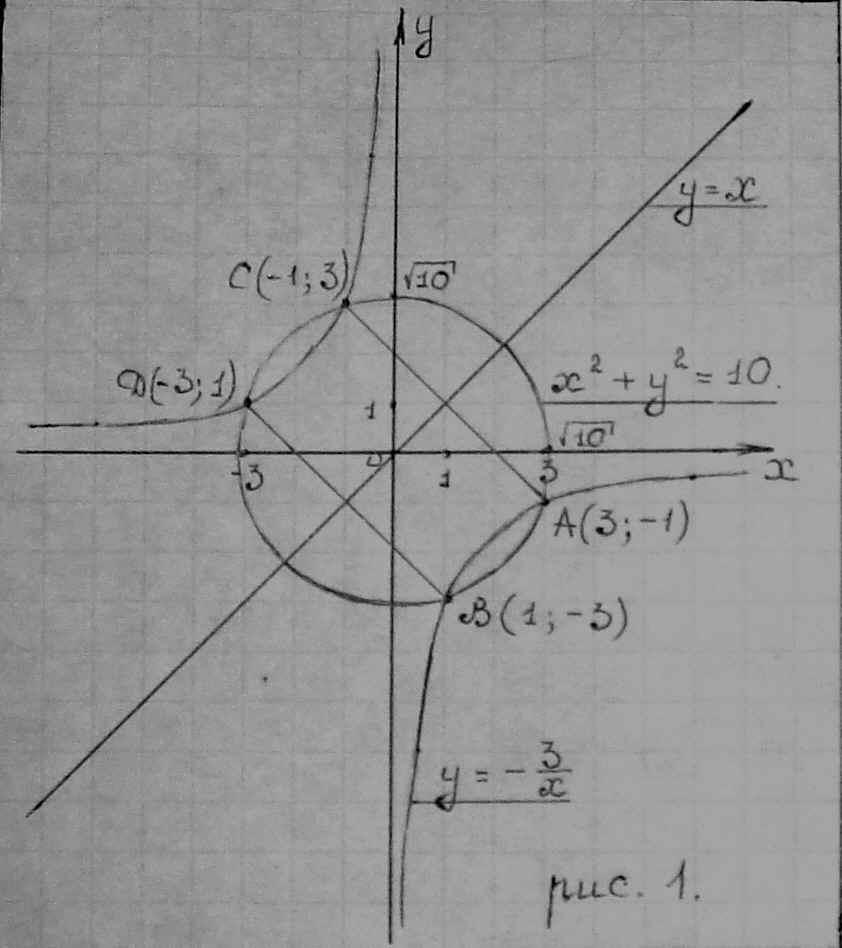
Рисунок 1

Графики изображены на рисунке 1.

Графики и пересекаются в четырех точках (они обозначены буквами А, В, С, Д), следовательно, данная система уравнений имеет четыре решения:

(3;-1), (-3;1), (-1;3), (1;-3).

Ответ: (3;-1), (-3;1), (-1;3), (1;-3).

Интересно заметить, что решения данной системы симметричны. Точки С и В и А и Д симметричны относительно начала координат. Точки С и А и Д и В симметричны относительно биссектрисы I и III координатных углов (прямой у=х), поэтому их координаты “меняются местами”

Решение ученика 2 группы.

Решить систему

Свое решение на доске показывает одна из групп:

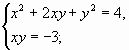
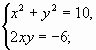
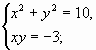
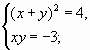(1)

Система (1) “распадается” на две более простые системы:

(2)

(3)

Каждое решение системы (1) является решением хотя бы одной из систем (2) или (3).И каждое решение системы (2) и (3) является решением системы (1).

Системы (2) и (3) является симметричными, решим каждую из них:

(1)

(2)

Пусть и корни уравнения	Пусть и корни уравнения
и его корни, Тогда (3;-1) и (-1;3)- решения системы (1).	и его корни, Тогда (-3;1) и (1;-3)- решения системы (2)

Для того чтобы понять содержательную сторону приведенного решения, обратимся к графической иллюстрации. На рис.2 в одной системе координат показано графическое решение систем.

 

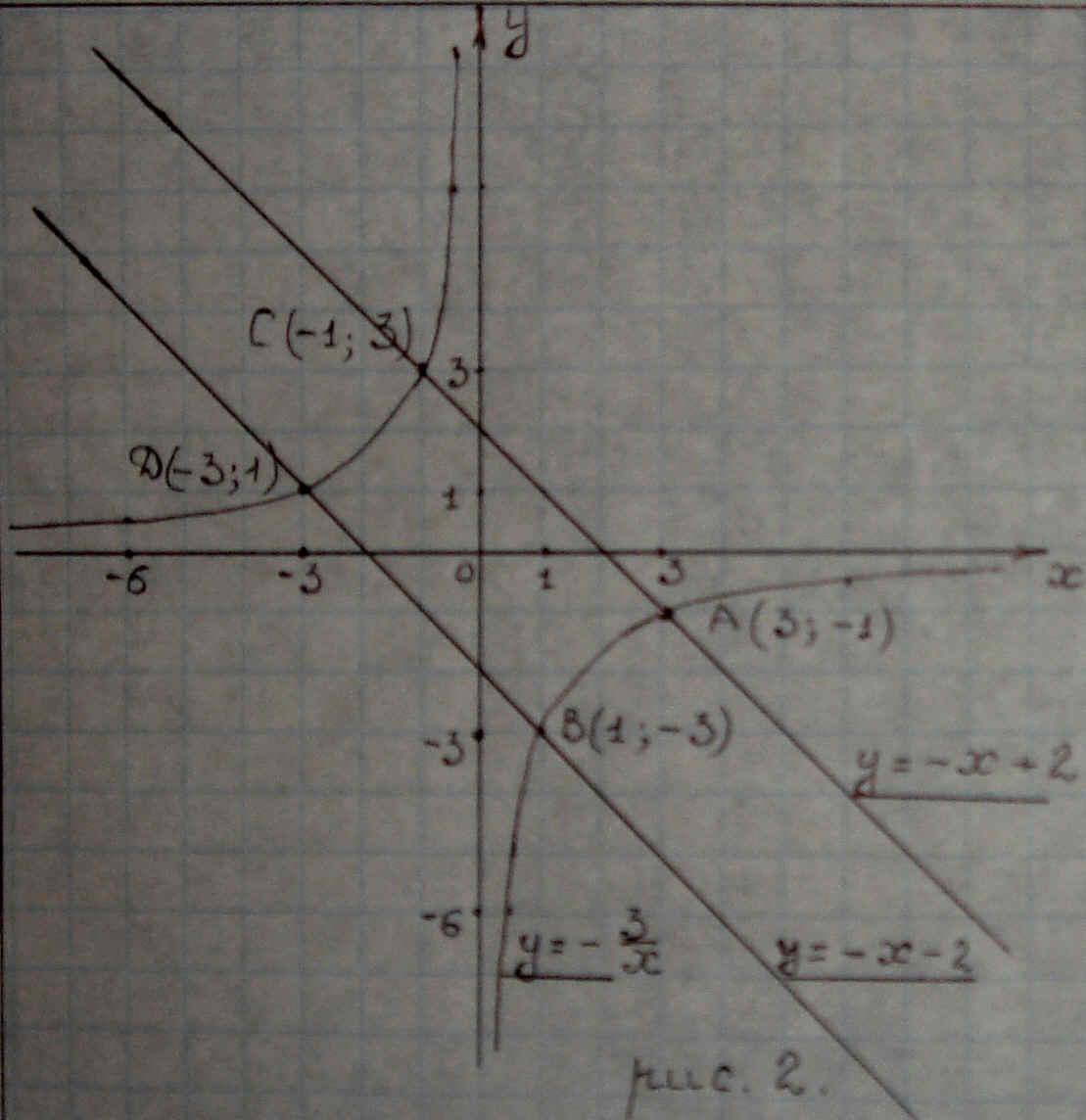
Рисунок 2

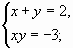и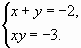

Каждая прямая х+у =2 и х+у =-2 пересекает гиперболу ху=-3 в двух точках, а всего мы имеем четыре точки пересечения (они обозначены буквами А, В, С, Д). Это те же точки, которые получились при пересечение гиперболы и окружности (смотри рис.1).

Ответ: (3;-1), (-3;1), (-1;3), (1;-3).

Еще один способ решения данной системы представил один из учеников3 группы.

Решение:

Сложим почленно первое уравнение системы сначала с уравнением 2ху=-6,а затем с уравнением -2ху=6.Получим систему:

Из первого уравнения получаем, что

х+у=2 или х+у =-2.

Из второго уравнения получаем, что

х-у=4 или х-у=-4.

Рассматривая каждое уравнение первой строки совместно с каждым уравнение второй строки приходим к четырем системам линейных уравнений:

Решив каждую из них получим следующие решения исходной системы:

(3;-1), (-3;1), (-1;3), (1;-3).

Решение проиллюстрировано графически на рис.3.

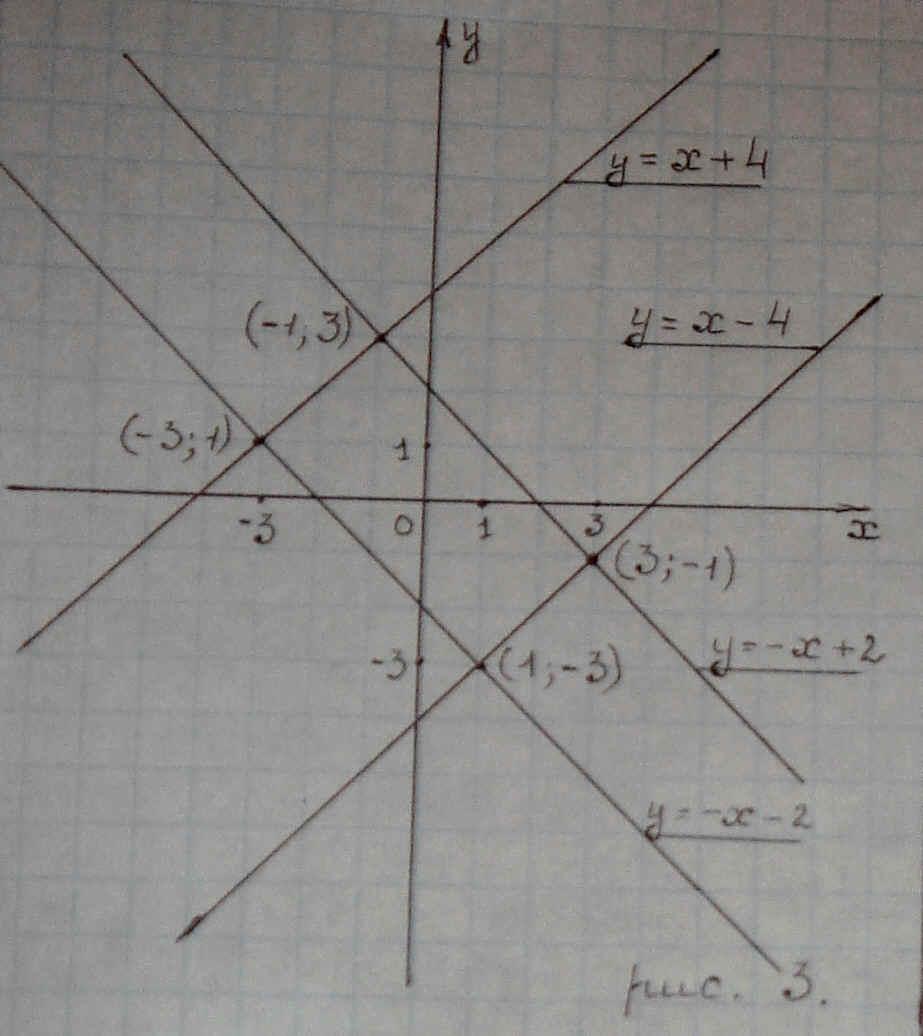
Рисунок 3

Теперь мы видим, что четыре прямые при попарном пересечении указывают нам те же самые точки, которые получились при пересечении окружности и гиперболы (смотри рис.1).

Ответ: (3;-1), (-3;1), (-1;3), (1;-3).

И еще разберем один из способов решения системы

Данная система является симметричной и решается она очень красиво с помощью введения новых переменных. Пусть , и учитывая, что ,получим:

Если u=-3, то или тогда получим:

и

Полученные системы тоже являются симметричными системами, которые мы уже решали. Итак,(3;1), (-1;3), (-3;1),(1;-3)-решения данной системы.

Мы рассмотрели пять различных способов решения одной и той же системы уравнений. Каждый выберет для себя способ, который ему больше всего понравился, самое главное - что каждый из Вас научился решать системы такого вида и поэтому эпиграфом домашнего задания могли служить слова Б.В.Гнеденко: “Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях”.

Разминка.

Учащимся предлагается решить тестовые задания (из КИМов ГИА),результаты решений записать в тетрадь. На выполнение задания отводится пять минут.

(слайд 5-8).

Самопроверка тестового задания (слайд 9).

Обратитесь к своим оценочным листам. Поставьте в них заработанную оценку и изобразите свое эмоциональное состояние с помощью “смайлика” улыбающегося, безразличного или грустного.

. Этап II Решение систем уравнений алгебраическими способами.

(слайд 10).

. Ваша задача состоит в том, чтобы поставить в соответствие каждому уравнению верный ответ. Системы уравнений обозначены буквами. Если все задания выполните правильно , вы прочитаете имя одного из древнегреческих математиков. На решения отводится 15 минут.

Четверо учащихся решают системы уравнений по образцам у доски.

1). Решите систему уравнений по образцу

Образец:

1. Выразим в уравнении первой степени х-5у=-2 одну переменную через другую х=-2+5у.

2. Подставим полученное выражение (-2+5у) в уравнение второй степени

(-2+5у)-у²=16.

1. Приведем уравнение к уравнению с одной переменной

-2+5у-у²=-16, -у²+5у-2+16=0, -у²+5у+14=0 ·(-1), у²-5у-14=0.

1. Решим квадратное уравнение

у²-5у-14=0, а=1; в=-5; с=-14, D=в²-4ас=(-5)²-4·1·(-14)=25+56=81=9²0 – два корня.

У_1;2= У₁= У₂=

1. Найдем значение второй переменной

Если У₁=7, то х₁=-2+5·7=33;

Если У₂= -2, то х₂=-2+5·(-2)=-2-10=-12.

(33;7); (-12; -2) – решения системы

Ответ: (33;7); (-12; -2)

2). Решить систему уравнений по образцу

Образец: Решить систему уравнений способом сложения.

1. Складываем почленно оба уравнения, получаем систему

2. Решим полученное уравнение с одной переменной 2х²=50

х²=50:2=25,

х=,

х₁=5; х₂= -5.

1. Найдем значение второй переменной

Если х₁=5, то 5²+3у²=28, 25+3у²=28, 3у²=28-25=3, у²=3:3=1, у₁=1, у₂= -1.

Если х₂= -5, то (-5)²+3у²=28, 25+3у²=28, 3у²=28-25=3, у²=3:3=1, у₁=1, у₂= -1.

Ответ: (5;1); (5;-1); (-5; 1); (-5;-1).

Решите по образцу

3).Решить систему уравнений по образцу

Образец: Решить систему уравнений способом подстановки.

1. Выразим в уравнении первой степени 2у-х=7 одну переменную через другую –х=7-2у,

х=2у-7

1. Подставим полученное выражение (2у-7) в уравнение второй степени

(2у-7)²-(2у-7)у-у²=29.

1. Приведем уравнение к уравнению с одной переменной

4у²-28у+49-2у²+7у-у²=29, у²-21у+49-29=0, у²-21у+20=0,

1. Решим квадратное уравнение

у²-21у+20=0, а=1; в=-21; с=20, D=в²-4ас=(-21)²-4·1·20=441-80=361=19²0 – два корня.

У_1;2= У₁= У₂=

1. Найдем значение второй переменной

Если У₁=20, то х₁=2·20-7=40-7=33;

Если У₂= 1, то х₂=2·1-7=-5.

(33;20); (-5; 1) – решения системы

Ответ: (33;20); (-5; 1)

Решите по образцу

4). Решить систему уравнений по образцу

Образец: Решить систему уравнений графическим способом.

1. В уравнении ху= 4 выразим переменную у через переменную х, получим .

2. Составим таблицу значений переменных для гиперболы

   х	-8	-4	-2	-1	1	2	4	8
   у		-1	-2	-4	4	2	1

3. Найдем координаты вершины параболы х=0, тогда у=0,5·0²-8=-8. КВП(0;-8)

4. Составим таблицу значений переменных для параболы у =0,5х²-8

х	-4	-2	-1	0	1	2	4
у	0	-6	-7,5	-8	-7,5	-6	0

у

х

Ответ: (-3,8; -1,2); (-0,6; -7,9); (4,2; 0,9) ;

Решите по образцу:

У=х²+1,

Ху=3.

Решение систем уравнений второго уровня.

Решить систему уравнений

x-5y=5,
x² -25y ²=-75.

Разложим левую часть второго уравнения системы на множители, используя формулу разности квадратов

а²–b²=(a+b)(a-b):

 х² -25y²=(x-5y)(x+5y)  

После этого наша система уравнений примет вид:
x-5y=5,
(x-5y)(x+5y)=-75.

Используя первое уравнение системы x-5y=5 , заменим во втором уравнении x-5y на его значение 5
x-5y=5,
 5(x+5y)=-75.  

Разделим левую и правую части второго уравнения системы на 5:
x-5y=5,

  x+5y=-15. (3)

Таким образом, мы получили линейную систему уравнений. Вычтем почленно из 1-ого уравнения 2-рое: -10y=20.Выразим отсюда y: y=-2. 

Теперь подставим у=-2 в одно из уравнений системы (3),

 например во второе:

x+5*(-2)=-15, x=-5.
  Ответ: x = -5, y = -2.

Решить систему уравнений

2x+3y=-8,

4x² +5xy+9y² =50. (1) 

 Возведем в квадрат обе части первого уравнения: (2x+3y)² =(-8)²  Используем формулу квадрата суммы:

(a+b)²  =a +2ab+b
(2x+3y)² =4x² +12xy+9y ² 

После этого наша система уравнений примет вид:

4x²+12xy+9y²=64,
 4x²+5xy+9y²=50. (2) 

Вычтем почленно из первого уравнения второе:

7xy=14,

 xy=2.

  Воспользуемся первым уравнением системы (1): 2x+3y=-8.

Выразим из этого уравнения x через y:

 2x=-3y-8
x=-1.5y-4  

Теперь подставим в уравнение xy=2 вместо x полученное выражение:

y(-1.5y-4)=2
-1.5y2  -4y-2=0  

 Найдем корни полученного квадратного уравнения: y1=-2 и y2=-2/3.
  Подставляя полученные значения в уравнение x=-1.5y-4, найдем соответствующие значения x:

x₁=-1.5*(-2)-4
x₁=-1

x₂=-1.5*(-2/3)-4
x₂=-3 

Ответ: x₁ = -1, y₁ = -2; x₂ = -3, y₂ = -2/3.

Решить систему уравнений

2x² -xy=-8,
 y² -2xy=32. (1) 

В первом уравнении вынесем за скобку x, а во втором y:
x(2x-y)=-8,
y(y-2x)=32.

  Домножим второе уравнение на -1:
x(2x-y)=-8,
 y(2x-y)=-32.  

Домножим первое уравнение на y, а второе на x:
xy(2x-y)=-8y,
xy(2x-y)=-32x.  

 Мы получили два уравнения, с одинаковой левой частью, следовательно, их правые части равны:
-8y=-32x   Выразим отсюда y: y=4x 

Подставим в уравнение x(2x-y)=-8 вместо y, полученное выражение:
    x(2x-4x)=-8
    x(-2x)=-8
-2x² =-8
x²=4 x₁=2  x₂=-2  

Подставляя полученные значения в уравнение y=4x,

найдем соответствующие значения y:

 y₁=4*2
_У1=8 y2=4*(-2)
y₂=-8 

Ответ: x₁ = 2, y₁ = 8; x₂ = -2, y₂ = -8. 

Решить систему уравнений 

x+4y=-2,
 x³ +64y³ =-56.

Используя формулу суммы кубов a³+b³=(a+b)(a²-ab+b²), разложим на множители     x³+64y³:
x³ +64y³ =(x+4y)(x² -4xy+16y² ). 

После этого система  примет вид:

 x+4y=-2,

(x+4y)(x² -4xy+16y² )=-56.

Подставляя во второе уравнение системы вместо x+4y его значение -2, мы получим:

x+4y=-2,
-2(x² -4xy+16y ²)=-56.

x+4y=-2,
 x ²-4xy+16y² =28.  

 Возведем в квадрат обе части первого уравнения x+4y=-2.  

 По формуле квадрата суммы

(a+b)² =a² +2ab+b² :
(x+4y)² =x² +8xy+16y²

Таким образом, мы получим систему уравнений:
x² +8xy+16y² =4,
x² -4xy+16y² =28. (3)

  Вычтем почленно из первого уравнения системы (3) второе:
8xy-(-4xy)=4-28
12xy=-24
xy=-2

  Воспользуемся первым уравнением системы (1) и выразим одно неизвестное через другое, допустим x через y:

 x+4y=-2
x=-4y-2  

 Подставим теперь в уравнение xy=-2 вместо x полученное выражение:

y(-4y-2)=-2
-4y² -2y+2=0
2y² +y-1=0

  Найдем корни полученного квадратного уравнения:
y₁=-1 y₂=0.5 

Подставляя полученные значения в уравнение x=-4y-2, найдем соответствующие значения x:

x₁=-4*(-1)-2
x₁=2

x₂=-4*0.5-2
x₂=-4 

Ответ: x₁ = 2, y₁ = -1; x₂ = -4, y₂ = 0.5

(слайд 11)

- Итак, вы получили имя ДИОФАНТ. Чем же знаменит он? Почему именно его имя я зашифровала в таблице?

Рассказ учителя.

Диофант Александрийский – один из самых своеобразных древнегреческих математиков. До сих пор не выяснены ни год рождения, ни дата смерти Диофанта; полагают, что он жил в 3 веке нашей эры. Из работ Диофанта самой важной является “Арифметика”, из 13 книг которой только 6 сохранились до наших дней. В сохранившихся книгах Диофанта содержится 189 задач с решениями. В пяти книгах содержатся методы решения неопределенных уравнений. Это и составляет основной вклад Диофанта в математику (слайд 12).

А вот о том, сколько же лет прожил Диофант вы мне ответите на следующем уроке, решив дома задачу текст которой у вас на парте,. Эта задача была найдена в одном из древних рукописных сборников задач в стихах, где жизнь Диофанта описывается в виде алгебраической загадки, представляющей надгробную надпись на его могиле.

Прах Диофанта гробница покоит; дивись ей – и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею 5 лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил ,
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.

Этап III. Решение систем уравнений графическим способом.

Тестирование. Три уровня сложности.

1 уровень.

Установите соответствие между формулой и графиком

1).

1. у= кх+в(к0)

2. у= кх(к

3. у=кх+в (к0)

4. у=кх (к0)

5. У=!х!

абв

гд

2).

а бв

1. У=ах² (а 0 ) г)д

2. У =к/х(к0)

3. У= к/х (к0)

4. У= х^1/2 , 5. У=ах² (а)

2 уровень.

“Проанализируйте уравнения, их графики и заполните таблицу”. В таблице записаны уравнения с двумя переменными, а ниже приведены их графики. Ваша задача состоит в том, чтобы поставить в соответствие каждому уравнению график. Системы уравнений обозначены буквами. Если все задания выполните правильно вы прочитаете имя одного из древнегреческих математиков.

3 уровень.

-Изображены графики некоторых уравнений, а справа записаны системы уравнений. Но в этой системе одного уравнения не хватает. Ваша задача заключается в том, чтобы

1. в систему вписать уравнение линии, изображенной на чертеже

2. дополнить чертеж графиком, уравнение которого уже записано в системе

3. найти решения данной системы графически.

В правом столбце таблицы записаны буквы, а рядом пара чисел. Каждая пара соответствует решению системы . Из полученных букв составьте фамилию великого французского ученого. Работает каждый индивидуально. Время работы 10 минут.

В это же время у доски 4 учащихся выполняют работу в парах (слайд 13).

- Возьмите свои оценочные листы, поставьте себе оценку за работу на третьем этапе урока и выразите свое эмоциональное состояние.

Этап IV.Исследовательская деятельность.

- На данном этапе урока нам предстоит с вами побывать в роли исследователей. Перед нами стоит задача: выяснить количество решений системы двух уравнений с двумя переменными в зависимости от параметра.

Индивидуальное домашнее задание , которое приготовил ученик(слайд 14,15).

Если , то система имеет единственное решение,

если , то система не имеет решений,

если , то система имеет бесконечно много решений.

При каких значениях параметра а система

а) имеет бесконечно много решений;

б) имеет единственное решение?

Решение:

а) , а = 4.

б) , а  4.

Решите систему уравнений:

Решение:

а)

, т.е. при m  1 система имеет единственное решение

,

б) , т.е. при m = 1 и n  1 исходная система решений не имеет.

в) , при m = 1 и n = 1 система имеет бесконечно много решений.

Ответ: если m = 1 и n  1, то решений нет;

если m = 1 и n = 1, то решений бесконечное множество, ;

если m  1 и n – любое, то

ИТОГ УРОКА.

Итак, сегодня мы с вами

• закрепили знания, умения и навыки по теме “Уравнения с двумя переменными второй степени и их графики. Решение систем уравнений с двумя переменными”.

• познакомились с великим ученым, который внес огромный вклад в развитие математики.

• приобрели начальные навыки исследовательской деятельности

Все ваши работы сложите в файл и сдайте.

Задание на дом (слайд 16-18).

-Осталось проверить барометр вашего настроения.

Урок окончен.