Симметрия. Осевая симметрия.
Содержание:
- Определение симметрии, виды симметрии.
- Осевая симметрия.
- Вывод. Теорема.
Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость в расположении частей.
Виды симметрии.
- 1. осевая симметрия
- 2. центральная
- 3. зеркальная
- 4. параллельный перенос.
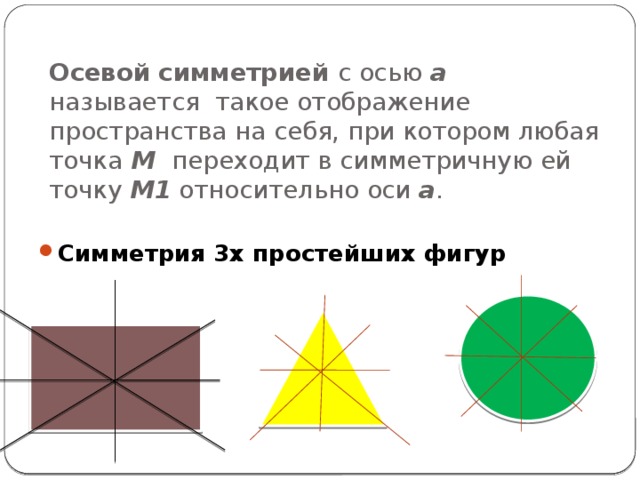
Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка M переходит в симметричную ей точку M1 относительно оси a .
- Симметрия 3х простейших фигур
Докажем , что осевая симметрия является движением.
Y
К
Z
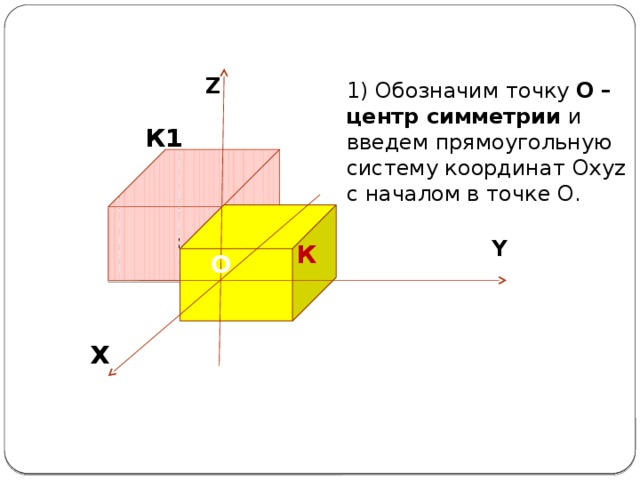
1) Обозначим точку О – центр симметрии и введем прямоугольную систему координат Оxyz с началом в точке О.
К1
O
O
X
Y
К
Z
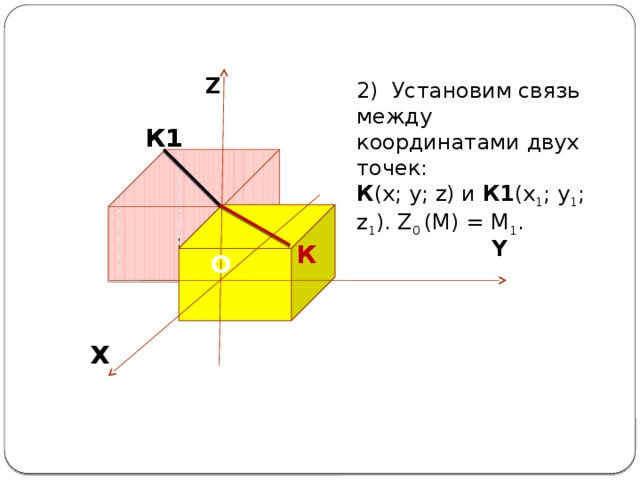
2) Установим связь между координатами двух точек:
К (x; y; z) и К1 (x 1 ; y 1 ; z 1 ). Z 0 (M) = M 1 .
К1
O
O
X
К
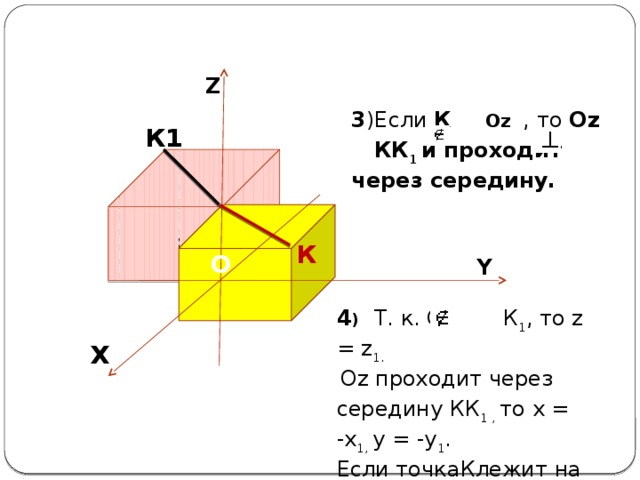
4 ) Т. к. Оz К 1 , то z = z 1.
Оz проходит через середину КК 1 , то х = -х 1, у = -у 1 .
Если точкаКлежит на оси Оz, то х 1 = х = 0, у 1 = у = 0, z 1 = z = 0.
Z
3 )Если К Оz , то Оz КК 1 и проходит через середину.
К1
O
O
Y
X
А 1 , В— В 1 , тогда А 1 (-x 1 ; -y 1 ; z 1 ), В 1 (-x 2 ; -y 2 ; z 2 ) Z B1 5) Рассмотрим А(x 1 ; y 1 ; z 1 ), В(x 2 ; y 2 ; z 2 ) B A1 O O X" width="640"
Y
A
6) А— А 1 , В— В 1 ,
тогда А 1 (-x 1 ; -y 1 ; z 1 ),
В 1 (-x 2 ; -y 2 ; z 2 )
Z
B1
5) Рассмотрим А(x 1 ; y 1 ; z 1 ),
В(x 2 ; y 2 ; z 2 )
B
A1
O
O
X
тогда АВ=А 1 В 1 , т.е. S оz - движение.
Y
A
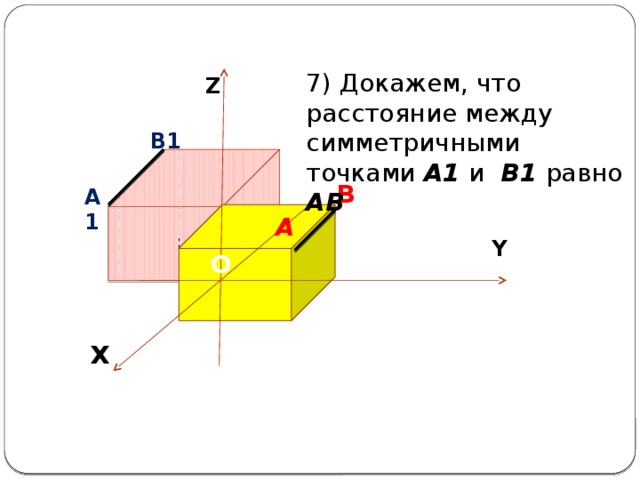
7) Докажем, что расстояние между симметричными точками А1 и В1 равно АВ
Z
B1
B
A1
O
O
X
тогда АВ=А 1 В 1 , т.е. S оz - движение.
тогда АВ=А 1 В 1 , т.е. S оz - движение , что и требовалось доказать.
По формуле расстояния между двумя точками находим :
