ОПОРНЫЕ КОНСПЕКТЫ ПО ГЕОМЕТРИИ (теоретический материал) для 7 класса

ОПОРНЫЕ КОНСПЕКТЫ ПО ГЕОМЕТРИИ (теоретический материал)

для учащихся 7 класса

1. Смежные углы

2. Вертикальные углы

3. Первый признак равенства треугольников

4. Второй признак равенства треугольников

5. Третий признак равенства треугольников

6. Признаки параллельности прямых

7. Свойства параллельных прямых

8. Равнобедренный треугольник. Равносторонний треугольник. Свойства равнобедренного треугольника.

9. Теорема о свойстве медианы равнобедренного треугольника

10. Сумма углов треугольника

1.СМЕЖНЫЕ УГЛЫ

Определение. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.

Теорема. Сумма смежных углов равна 180.

Дано: АОВ и ВОС – смежные.

Доказать: АОВ + ВОС = 180.

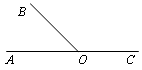
Доказательство

АОВ+ВОС=АОС, АОС – развёрнутый, значит, АОВ+ВОС = 180, что и требовалось доказать.

Следствие. Если смежные углы равны, то они прямые.

Дано: АОВ и ВОС – смежные. АОВ = ВОС.

Доказать: АОВ и ВОС – прямые.

Доказательство

АОВ + ВОС=180, АОВ = ВОС = = 90, значит, АОВ и ВОС – прямые, что и требовалось доказать.

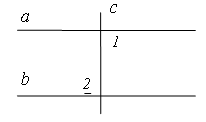
2.ВЕРТИКАЛЬНЫЕ УГЛЫ

Определение. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Теорема. Вертикальные углы равны.

Дано: 1 и 3, 2 и 4 – вертикальные.

Доказать: 1 = 3, 2 = 4.

Доказательство

1 и 2, 3 и 2 – смежные, значит

аналогично , ч. т. д.

Определение. Угловая мера меньшего из вертикальных углов называется углом между прямыми.

Угол между пересекающимися прямыми.

3.ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Теорема. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Дано: ABC;

Доказать: ABC =

Доказательство:

А = А₁, поэтому можно наложить ABC на А₁В₁С₁, так что вершина А совместится с вершиной А₁, а стороны АВ и АС наложатся соответственно на лучи А₁В₁ и А₁С₁.

АВ = А1В1	АС = А1С1
АВ	АС	В	С		ВС	АВС
Совместятся при наложении
А1В1	А1С1	В1	С1	В1С1		А1В1С1

Т. о., АВС = А₁В₁С₁, ч. т. д.

4.ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Теорема. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Дано: АВС, А₁В₁С₁, АВ = А₁В₁, А = А₁, В = В₁.

Доказать: АВС = А₁В₁С₁.

Доказательство

АВ = А₁В₁, поэтому можно наложить АВС на А₁В₁С₁ так, чтобы вершина А совместилась с вершиной А₁, сторона АВ – со стороной А₁В₁, а вершины С и С₁ оказались по одну сторону от прямой А₁В₁.

А = А1	В = В1
Луч АС	Луч ВС		С = АС  ВС	АС	ВС	АВС
Совместятся при наложении
Луч А1С1		Луч В1С1	С1 = А1С1  В1С1	А1С1	В1С1	А1В1С1

Т. о., АВС = А₁В₁С₁, ч. т. д.

5.ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Дано: АВС, А₁В₁С₁, АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁.

Доказать: АВС = А₁В₁С₁.

Доказательство

АВ = А₁В₁, поэтому можно приложить АВС к А₁В₁С₁ так, чтобы вершина А совместилась с вершиной А₁, вершина В – с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой А₁В₁.

Возможны три случая: луч С₁С проходит внутри ; луч С₁С проходит вне А₁С₁В₁; луч С₁С совпадает с одной из сторон .

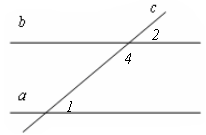
6.ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ

Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Дано: а с = А, b с = В, 1 и 2 накрест лежащие, 1 = 2

Доказать: а || b.

1. Если 1 = 2 = 90, то a  АВ и b АВ, тогда а || b.

1. Пусть углы 1 и 2 не прямые.

2. Разделим отрезок АВ пополам, получим О.

3. Проведем ОН  a.

4. На прямой b от точки В отложим ВН₁ = АН и проведем отрезок ОН₁.

5. ОНА = ОН₁В по двум сторонам и углу между ними (ОА = ОВ, АН = ВН₁, 1 = 2).

6. 3 = 4, 5 = 6 = 90

7. 3 = 4, поэтому точки Н₁, О₁, Н лежат на одной прямой.

8. а  НН₁ и b  НН₁, значит, а || b, ч. т. д.

Рассмотрим особо пункт 6.

Пусть точки Н, О и Н₁ не лежат на одной прямой, тогда продолжим ОН, получаем: НМ  АВ = О. НОА = ВОМ как вертикальные, но НОА = ВОН₁, значит, ВОМ = ВОН₁ и лучи ОН₁ и ОМ совпадают.

Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Дано: а  с, b  с, 1 и 2 соответственные. 1=2. Доказать: а || b.

Доказательство

1. 2 = 3 как вертикальные.

1. 2 = 1 по условию.

2. Значит, 1 = 3.

3. Но 1 и 3 накрест лежащие, поэтому а || b, ч. т. д.

Теорема. Если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

Дано: а  с, b  c. 1 и 4 – односторонние. 1 + 4 = 180. Доказать: а || b.

Доказательство

1. 3 и 4 – смежные, значит, 3 + 4 = 180.

1. 1 + 4 = 180 по условию.

2. Отсюда 1 = 3.

3. Но 1 и 3 накрест лежащие, поэтому а || b, ч. т. д.

7.СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

Теорема. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Дано: а || b. а  с = М. b  с = N. 1 и 2 накрест лежащие. Доказать: 1 = 2.

Доказательство

(методом от противного)

1. Пусть 1 2, тогда...

1. Отложим от луча МN угол РМN, равный углу 2 так, чтобы РМN и 2 были накрест лежащие при пересечении прямых РМ и в секущей МN.

РМN = 2 РМ || b. Мы получили, что РМ  а, РМ || b и а || b, что противоречит аксиоме параллельных.

1. Поэтому 1 = 2, ч. т. д.

Следствие. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Дано: а || b. с  а Доказать: с  b.

Доказательство

1. с  а, а || b  с  b

1. 1 = 2 как накрест лежащие при параллельных a, b и секущей с.

2. 1 = 902=90, т. е. с  b, ч. т. д.

Теорема. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Дано: а || b; с  а; с  b. 1 и 2 накрест лежащие. Доказать: 1 = 2.

Доказательство

1. а || b, поэтому 1 = 3 как накрест лежащие при параллельных а, b и секущей с.

1. 2 = 3 как вертикальные.

2. 1 = 2, ч. т. д.

Теорема. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180.

Дано: а || b, с  а, с  b. 1 и 4 односторонние. Доказать: 1 + 4 = 180.

Доказательство

1. а || b, поэтому 1 = 2 как соответственные при параллельных а, b и секущей с.

1. 2 и 4 – смежные, значит 2 + 4 = 180

8.РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК. РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

Определение. Треугольник называется равнобедренным, если две его стороны равны.

Основание АС.

Боковые стороны АВ и ВС.

Периметр Р = 2АВ + АС.

Углы при основании А и В.

Угол при вершине В.

Определение. Треугольник, все стороны которого равны, называется равносторонним.

АВ = ВС = АС

Свойство 1 равнобедренного треугольника

Теорема. В равнобедренном треугольнике углы при основании равны.

Дано: АВС – равнобедренный (АВ = АС).

Доказать: В = С.

Доказательство

Проведем биссектрису AD (1 = 2).

9.ТЕОРЕМА О БИССЕКТРИСЕ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА

Свойство 2 равнобедренного треугольника

Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Дано: АВС – равнобедренный, АВ = АС, AD – биссектриса.

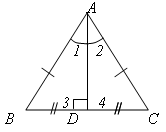
Доказать: 1) AD – медиана, 2) AD – высота.

Доказательство

1. По условию AD – биссектриса АВС, поэтому 1 = 2.

3. BD = CD, AD – медиана АВС, ч. т. д.

4. 3 = 4

Поэтому AD – высота АВС, ч. т. д.

Мы установили, что медиана, биссектриса и высота треугольника совпадают.

Справедливы теоремы:

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

10.СУММА УГЛОВ ТРЕУГОЛЬНИКА

Теорема. Сумма углов треугольника равна 180.

Дано: АВС. Доказать: А + В + С = 180.

Доказательство

1. Проведем а || АС.

1. 1 и 4, 3 и 5 – накрест лежащие. АС || а, поэтому 1 = 4, 3 = 5.

2. 4 + 2 + 5 = 180, значит, 1 + 2 + 3 = 180, ч. т. д.

Определение. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

Следствие 1. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: АВС. ВСD – внешний. Доказать: ВСD = 1 + 2

Доказательство

1. 4 + 3 = 180 по свойству смежных углов.

1. 1 + 2 + 3 = 180 по теореме о сумме углов треугольника.

2. 4 = 1 + 2, ч. т. д.

Следствие 2. Если два угла одного треугольника соответственно равны двум углам другого, то и третьи углы равны.