Неевклидова геометрия римана в факультативном курсе геометрии 11-го класса физмат школы

Неевклидова геометрия Римана

     Сферическая геометрия и неевклидова геометрия Римана. Огромное впечатление, произведенное на умы математиков открытием Лобачевского, Бойяи и Гаусса, быть может, было бы несколько менее сильным, если бы люди заметили, что еще задолго до Лобачевского они фактически уже владели содержательной геометрической схемой, отличной от традиционной геометрии Евклида, т. е. уже знали одну из неевклидовых геометрий. Однако твердое убеждение всех ученых в универсальности системы Евклида не позволило им оценить по достоинству тот запас знаний, которым они располагали. Именно поэтому первым примером геометрической системы, отличной от классической геометрии Евклида, считается обычно неевклидова геометрия Лобачевского. Значительно же более простая схема, по существу разработанная с большими деталями за много веков до Лобачевского, связывается обычно с именем гениального немецкого математика Бернхарда Римана, впервые обратившего внимание на родство этой схемы с классической геометрией Евклида и неевклидовой геометрией Лобачевского. Мы, однако, здесь не будем следовать истории вопроса и изложим более простую схему Римана до геометрии Лобачевского.

     Когда говорим, что неевклидова геометрия Римана была известна задолго до открытия Лобачевского, имеем в виду тесную связь ее со сферической геометрией (геометрией на плоскости сферы). Основные факты сферической геометрии были основательно изучены еще в древности в связи с задачами астрономии. Поскольку поверхность земли приближенно имеет форму сферы, можно утверждать, что "земная геометрия" также является геометрией сферической (это реально ощущается при измерениях, затрагивающих значительные участки земной поверхности).

     Роль прямых линий на сфере, т. е. самых коротких линий, соединяющих две точки сферы, играют так называемые большие окружности - сечения сферы плоскостями, проходящими через ее центр (см. Рис. 1). Углы между большими окружностями, как и углы между любыми другими линиями на сфере, принимаются равными углам между касательными к этим линиям в точках пересечения. Роль треугольников и многоугольников в сферической геометрии играют сферические треугольники и многоугольники, образованные дугами больших окружностей (см. Рис. 2).

Под расстоянием между двумя точками на сфере понимается длина меньшей из двух дуг большой окружности, соединяющей эти точки. Это определение следует видоизменить лишь для случая диаметрально противоположных точек A и A₁ сферы; для них существует бесконечно много соединяющих их дуг больших окружностей, и все они имеют одну и ту же длину πr (где r - радиус сферы), которую и принимаем за расстояние между A и A₁.

Роль окружностей в сферической геометрии играют так называемые малые окружности, т. е. сечения сферы плоскостями, не проходящими через ее центр. Ясно, что любую окружность (и большую и малую) можно в сферической геометрии определить как множество точек, удаленных от фиксированной точки Q на постоянное расстояние ρ; точка Q называется при этом центром (или полюсом) окружности, а расстояние ρ - ее радиусом. У каждой окружности на сфере имеются два полюса Q₁, Q₂ (являющихся диаметрально противоположными точками сферы, Рис. 3) и соответственно этому два радиуса ρ₁, ρ₂. Если эти радиусы различны, то имеем малую окружность, если же они совпадают (и равны πr/2), то - большую окружность.

     Большие и малые окружности сферы аналогичны прямым и окружностям на плоскости еще и в том отношении, что существуют движения сферы (повороты, Рис. 4), переводящие их в себя. Из этого ясно, что большие и малые окружности являются "однородными" линиями, т. е. во всех своих точках они устроены совершенно одинаково.

     Однако между геометрией на сфере и геометрией на плоскости имеется и одно существенное различие. Мы знаем, что через каждые две точки плоскости проходит единственная прямая линия; другими словами, никакие две прямые не могут пересечься в двух точках. В противоположность этому каждые две большие окружности сферы пересекаются в двух (диаметрально противоположных) точках. Это обстоятельство резко отличает сферическую геометрию как от евклидовой геометрии, так и от неевклидовой геометрии Лобачевского. Для того чтобы устранить его, условимся называть "точкой" сразу пару диаметрально противоположных точек сферы. Полученный геометрический образ - сферу, понимаемую как множество пар диаметрально противоположных точек, - мы и назовем неевклидовой плоскостью Римана. Под "прямыми" неевклидовой геометрии Римана будем понимать большие окружности сферы (рассматриваемые как множество пар диаметрально противоположных точек). Условимся, далее, принимать за "расстояние" между двумя "точками" A и B плоскости Римана (не превосходящее четверти большой окружности) расстояние между соответствующими им точками сферы (так что расстояние между "точками", изображаемыми имеющимися на Рис. 5 парами A, A₁ и B, B₁, равно дугам AB или A₁B₁, но не AB₁!). При таком определении полная длина "прямой" будет равна πr, но не 2πr (т. к., пройдя по "прямой" путь AA₁, равный πr, придем к "точке" A₁, совпадающей с исходной "точкой" A, Рис. 6).

Под "углами" между "прямыми" неевклидовой геометрии Римана будем понимать углы между отвечающими этим "прямым" большими окружностями сферы. "Окружность" с центром Q и радиусом ρ естественно определить как множество "точек", удаленных от Q на "расстояние" ρ: на сфере она изображается малой окружностью (точнее, парой диаметрально противоположных малых окружностей, Рис. 7). "Движения" неевклидовой геометрии Римана можно описать как вращения сферы: так как каждое вращение сферы переводит две ее диаметрально противоположные точки снова в диаметрально противоположные точки, то "движение" представляет собой "точечное" преобразование плоскости Римана, переводящее каждую ее "точку" снова в "точку".

     Плоскость Римана можно также представлять себе как полусферу, склеенную весьма своеобразным образом - так, чтобы совпали диаметрально противоположные точки ограничивающей ее окружности (см. Рис. 8).

     Введем теперь в пространстве прямоугольные координаты x, y, z с началом в центре рассматриваемой сферы. Для этого проведем через центр O сферы три взаимно перпендикулярные плоскости, например горизонтальную и две вертикальные (см. Рис. 9), и условимся характеризовать каждую точку пространства тремя числами x, y, z, абсолютные величины которых равны расстояниям этой точки от указанных плоскостей, а знаки положительны для точек, расположенных по одну сторону от соответственной плоскости, и отрицательны по другую сторону от этой плоскости.

Так, например, координата x по абсолютной величине равна расстоянию от профильной вертикальной плоскости; она положительна, когда данная точка лежит справа от этой плоскости, и отрицательна, когда точка лежит слева. Координата y по абсолютной величине равна расстоянию от фронтальной вертикальной плоскости; она положительна для точек, расположенных перед этой плоскостью, и отрицательна для точек, расположенных за ней. Координата z по абсолютной величине равна расстоянию от горизонтальной плоскости; она положительна для точек, лежащих над этой плоскостью, и отрицательна для точек, лежащих под ней.

     Расстояние OM от начала координат O до произвольной точки M с координатами x, y, z определяется соотношением

OM² = x² + y² + z².     (1)

В самом деле, обозначив через P основание перпендикуляра, опущенного из точки M на горизонтальную плоскость, получим, в силу теоремы Пифагора, OM² = OP² + z², а OP² = x² + y², откуда и следует, что OM² =x² + y² + z². Если радиус нашей сферы равен r, то, в силу соотношения (1), координаты всех точек сферы удовлетворяют условию

x² + y² + z² = r².     (2)

"Точки" неевклидовой плоскости Римана можно описать тем же уравнением, если только условиться считать, что M(x, y, z) и M₁(-x, -y, -z) - это одна точка.

     Расстояние M₁M₂ между двумя произвольными точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂) пространства определяется по общей формуле

     (3)

(частным случаем которой является формула (1)), а угол φ между двумя отрезками OM₁ и OM₂, исходящими из точки O, - по формуле

     (4)

     Для того чтобы убедиться в справедливости этих формул, напомним, что если a и b - два вектора с координатами x₁, y₁, z₁ и x₂, y₂, z₂, то

ab = ab cos φ = x₁x₂ + y₁y₂ + z₁z₂

(где φ - угол между векторами a и b) и, в частности,

Формула (3) вытекает теперь из того, что (поскольку вектор имеет координаты x₂ - x₁, y₂- y₁, z₂ - z₁), а формула (4) - из того, что (поскольку векторы и имеют координатыx₁, y₁, z₁ и x₂, y₂, z₂).

     Если M₁ и M₂ - точки нашей сферы, то обычное расстояние между ними измеряется по формуле (3). Расстояние же ω между этими точками, измеренное по большой окружности сферы, в соответствии с соглашениями, принятыми в сферической геометрии, равно углу φ между отрезками OM₁ и OM₂, умноженному на радиус r сферы; поэтому, согласно соотношениям (2) и (4), это расстояние вычисляется по формуле

     (5)

     Для определения "расстояния" между двумя "точками" M₁ и M₂ неевклидовой геометрии Римана можно воспользоваться той же формулой (5), где только надо учесть, что если ω окажется больше πr/2 (т. е. если уголφ будет тупым), то одну из точек M₁, M₂ надо будет заменить центрально-симметричной (т. е. изменить знаки у чисел x₁, y₁, z₁ или у чисел x₂, y₂, z₂). Отсюда получаем следующую формулу для "расстояния" между двумя "точками" неевклидовой плоскости Римана:

     (6)

     Основные понятия неевклидовой геометрии Римана. Принцип двойственности. Далее будем говорить лишь о неевклидовой геометрии Римана, в соответствии с чем откажемся от кавычек, указывающих на образы этой геометрии. При этом будем все время иметь в виду тесную связь рассматриваемой геометрии со сферической, позволяющую выводить все теоремы неевклидовой геометрии Римана из известных факторов сферической геометрии.

     Мы не ставим перед собой задачи дать полный перечень аксиом геометрии Римана. Укажем только, что основная аксиома "через всякие две точки можно провести прямую и притом только одну" евклидовой геометрии сохраняет силу и в геометрии Римана; но наряду с ней здесь имеет место также и аксиома "всякие две прямые пересекаются в точке и притом только в одной" (на сфере всякие две большие окружности пересекаются в двух диаметрально противоположных точках, но после отождествления диаметрально противоположных точек эти две точки превращаются в одну). Из этой аксиомы вытекает, что на неевклидовой плоскости Римана выполняется V постулат Евклида: если на этой плоскости пересекаются всякие две прямые, то в том числе пересекаются и прямые, удовлетворяющие условию V постулата^*. Однако на неевклидовой плоскости Римана не выполняются аксиомы порядка евклидовой плоскости, так как в случае неевклидовой плоскости Римана каждую из трех точек прямой можно считать лежащей между двумя другими, подобно тому как это имеет место для трех точек евклидовой окружности. По этой причине на неевклидовой плоскости Римана не проходит приведенное выше доказательство теоремы Лежандра о том, что сумма углов треугольника не превосходит 180°. Напротив, из того, что сумма углов сферического треугольника больше 180° вытекает, что сумма углов любого треугольника на неевклидовой плоскости Римана больше 180°. Поэтому утверждение Лежандра о том, что V постулат эквивалентен предположению о равенстве суммы углов треугольника двум прямым углам, справедливо только при выполнении остальных аксиом геометрии Евклида - на неевклидовой плоскости Римана, на которой V постулат выполняется, но не выполняются аксиомы порядка геометрии Евклида, эти утверждения уже не эквивалентны.

   __________________________________

^*   Впрочем, заключительная часть V постулата, указывающая, по какую сторону от секущей пересекутся две встречающие ее прямые, в неевклидовой геометрии Римана теряет смысл, поскольку прямая не разбивает неевклидовой плоскости Римана на две части.

Если на сфере у каждой большой окружности имеются два диаметрально противоположных полюса, то на неевклидовой плоскости Римана у каждой прямой имеется только один полюс. Прямую неевклидовой плоскости Римана можно рассматривать как множество всех точек, отстоящих от полюса на расстоянии πr/2. Если на Рис. 7 будем приближать расстояние ρ к πr/2, то увидим, что окружность радиуса ρ с центром Q будет приближаться к прямой с полюсом Q с двух сторон и в пределе окружность перейдет в прямую, пройденную не один, а два раза ("дважды взятую" прямую). Это соответствует тому, что длина окружности радиуса ρ, равная , при стремлении ρ к πr/2 стремится к 2πr, а длина прямой на неевклидовой плоскости Римана равна πr.

     Из свойств сферических окружностей вытекает, что все перпендикуляры к одной прямой на неевклидовой плоскости Римана пересекаются в полюсе этой прямой. Далее, всякие две прямые на плоскости Римана обладают общим перпендикуляром, полюсом которого является точка пересечения этих прямых. Из этого вытекает, что при r = 1 угол^* между двумя прямыми a и b (см. Рис. 10) равен расстоянию между точками M иN их пересечения с их общим перпендикуляром c, а также равен расстоянию между полюсами A и B этих прямых. Последний факт показывает, что прямые неевклидовой плоскости Римана находятся во взаимно однозначном соответствии с ее точками - полюсами этих прямых, причем углы между прямыми равны расстояниям соответствующих точек. Таким образом, прямые неевклидовой плоскости Римана, если считать углы между ними расстояниями, образуют модель той же плоскости.

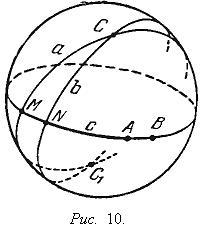
     Последнее обстоятельство можно пояснить также следующим образом. Рассмотрим своеобразное "преобразование" неевклидовой плоскости Римана, сопоставляющее каждой прямой a этой плоскости определенную точку A - полюс прямой a, а каждой точке A - прямую a, полюсом которой является точка A (эта прямая называется полярой точки A). Если рассматривать множество точек и прямых неевклидовой плоскости Римана как множество пар точек и больших окружностей сферы, то это преобразование сводится к замене каждой большой окружности парой ее полюсов и каждой пары диаметрально противоположных точек - большой окружностью (являющейся "экватором" сферы, если наши точки принять за "северный полюс" и "южный полюс"). Радиус сферы примем равным 1; это равносильно такому выбору единицы измерения длин на плоскости Римана, при котором длина прямой оказывается равной π. Соответствующее преобразование, заменяющее прямые точками, а точки прямыми, называется полярным преобразованием. В силу доказанного выше, две точки A и B переводятся полярным преобразованием в такие прямые a и b, что расстояние между A и B равно углу между a и b и наоборот; далее, если точки A и B принадлежат прямой c, то полярное преобразование переводит их в прямые a и b, пересекающиеся в точке C, отвечающей, в силу полярного преобразования, прямой c (см. Рис. 10).

     Существование полярного преобразования с такими замечательными свойствами обеспечивает выполнение в неевклидовой геометрии Римана принципа двойственности, заключающегося в следующем: если заменить в любом предложении неевклидовой геометрии Римана слова "точка", "лежит на", "расстояние" соответственно словами "прямая", "проходит через", "угол" и наоборот, то придем к новому предложению, также являющемуся правильным. Для доказательства достаточно подвергнуть выражающий первое предложение чертеж, а также все относящиеся к нему рассуждения полярному преобразованию. Предложения, получаемые одно из другого таким образом, называются двойственными друг другу. Так, например, аксиоме о том, что каждые две точки неевклидовой плоскости Римана принадлежат единственной прямой, двойственна аксиома: каждые две прямые неевклидовой геометрии Римана пересекаются в одной точке. Другие примеры двойственных друг другу предложений будут приведены далее.

   __________________________________

^*   Здесь, разумеется, говорится о радианной мере угла.

Примеры теорем неевклидовой геометрии Римана. Площадь треугольника и многоугольника.Неевклидова геометрия Римана имеет много общего с обычной геометрией Евклида. Так, например, здесь также справедливы теоремы о сравнительной длине сторон треугольника (каждая сторона меньше суммы двух других и больше их разности), о свойствах равнобедренного треугольника, о замечательных точках треугольника. Справедливы также и признаки равенства треугольников; только наряду с "третьим признаком равенства треугольников" (два треугольника равны, если стороны одного соответственно равны сторонам другого) в неевклидовой геометрии Римана имеет место еще так называемый "четвертый признак равенства треугольников": два треугольника равны, если углы одного из них соответственно равны углам второго. (С этим связано отсутствие в неевклидовой геометрии Римана преобразований подобия^*.) Первый и второй признаки равенства треугольников доказываются так же, как и в случае евклидовой геометрии: с использованием "неевклидовых движений", роль которых играют повороты неевклидовой плоскости Римана вокруг точки (см. выше Рис. 4) и симметрии относительно прямой (см. Рис. 11). Третий признак равенства треугольников также может быть доказан с помощью обычного приема - с использованием теорем о равнобедренном треугольнике, вывод которых не составляет труда (отметим, что симметрия относительно биссектрисы AD равнобедренного треугольника ABC, где AB = AC, переводит треугольник ABD в треугольникACD, Рис. 12). Наконец, четвертый признак равенства треугольников получается из третьего с помощью принципа двойственности.

     Теоремы о точке пересечения биссектрис треугольника ABC и о точке пересечения перпендикуляров, восстановленных к сторонам треугольника в их серединах, доказываются в точности так же, как в геометрии Евклида; первая из этих точек является центром вписанной в треугольник ABC окружности (см. Рис. 13, а), а вторая - центром описанной окружности (см. Рис. 13, б).

   __________________________________

^*   Отсутствие преобразований подобия в неевклидовой геометрии Римана можно также усмотреть из того, что на неевклидовой плоскости Римана каждая прямая имеет конечную длину πr, а вся плоскость - конечную площадь.

До сих пор мы больше говорили о тех теоремах неевклидовой геометрии Римана, которые аналогичны известным теоремам евклидовой геометрии. Для того чтобы дать представление о различии этих двух геометрий, остановимся на вопросе о площади многоугольника в неевклидовой геометрии Римана. Вспомним прежде всего, что в этой геометрии сумма углов треугольника всегда больше π. Отсюда можно вывести, что сумма углов n-угольника в неевклидовой геометрии Римана всегда больше (n - 2)π. В самом деле, каждый n-угольник можно разбить на n - 2 треугольников непересекающимися диагоналями (это относится как к неевклидовой геометрии Римана, так и к обычной геометрии Евклида и, разумеется, нуждается в доказательстве, которое здесь опускаем; случай n = 7 изображен на Рис. 14).

При этом сумма углов n-угольника равна сумме всех углов всех n - 2 треугольников; отсюда и вытекает, что сумма углов n-угольника в неевклидовой геометрии Римана всегда больше (n - 2)π. (Из аналогичных соображений вытекает, что в евклидовой геометрии сумма углов любого, может быть невыпуклого, n-угольника равна (n - 2)π.)

     Задача измерения площадей состоит в том, чтобы сопоставить каждому многоугольнику M некоторое числоS(M) - площадь этого многоугольника - с соблюдением следующих требований:

     а) положительность: для любого многоугольника M (содержащего внутренние точки) S(M) 0;

     б) инвариантность: если многоугольники M₁ и M₂ равны, то S(M₁) = S(M₂);

     в) аддитивность: если многоугольник M разбит на неперекрывающиеся части M₁ и M₂, то S(M) = S(M₁) +S(M₂);

     г) нормировка: для многоугольника M₀, признанного "единичным", S(M₀) = 1 (разумеется, все сказанное одинаково относится как к геометрии Евклида, так и к неевклидовой геометрии Римана^*).

   ___________________________________

^*   Такое (аксиоматическое) определение площади является осмысленным лишь в том случае, если действительно существует функция S, сопоставляющая каждому многоугольнику M число S(M) с указаными свойствами, и притом такая функция имеется лишь одна (т. е. указанные свойства а) - г) определяют функциюS однозначно). В неевклидовой геометрии Римана также существует теорема о том, что условия а) - г) однозначно определяет функцию S (площадь), но доказательство ее здесь не приводим. Впрочем, существование функции S будет ясно из дальнейшего, т. к. мы укажем величину (угловой избыток), удовлетворяющую условиям а) - г). Единственность же позволит утверждать, что указанная величина (угловой избыток) как раз и является площадью, поскольку, кроме нее, не существует никакой другой функции, удовлетворяющей условиям а) - г). Таким образом, единственность является важным элементом при построении теории площадей, и если мы опускаем здесь доказательство единственности, то не из-за его малой значимости, а лишь из-за нежелания перегружать статью.

  Очень просто указать число, удовлетворяющее наиболее важным условиям б) и в), - в качестве него можно взять угловой избыток (эксцесс) в (M) рассматриваемого n-угольника M, т. е. превышение суммы его углов над (n - 2)π:

ε(M) = A₁ + A₂ + ... + A_n - (n - 2)π

(здесь A₁, A₂, ..., A_n - углы n-угольника, измеренные в радианной мере). В самом деле, поскольку равные многоугольники M₁ и M₂ имеют одинаковые углы, то и избытки их, очевидно, равны:

ε(M₁) = ε(M₂);

таким образом, свойство инвариантности выполнено.

Пусть теперь n-угольник M разбит ломаной линией A₁B₁B₂ ... B_iA_k на два меньших многоугольника M₁ и M₂(см. Рис. 15).

Мы можем считать, что точки A₁ и A_k являются вершинами n-угольника M. В самом деле, если бы, скажем, точка A₁ принадлежала стороне многоугольника M, то мы могли бы M объявить (n+1)-угольником с фиктивной вершиной A₁ и углом при этой вершине, равным π; это не изменило бы углового избытка ε(M) многоугольникаM, поскольку сумма углов увеличилась на π и величина (n - 2)π - также на π. Теперь имеем (см. Рис. 15, где углы многоугольника M₁ отмечены одной дугой, а соответствующие углы многоугольника M₂ - двумя дугами):

и

Складывая эти выражения и учитывая, что и , получаем

ε(M₁) + ε(M₂) = A₁ + A₂ + ... + A_k + A_k+1 + ... + A_n + i · 2π - (k + i - 2)π - (n - k + i)π = A₁ + A₂ + ... + A_n - (n - 2)π =ε(M),     (7)

что и доказывает выполнение для углового избытка свойства аддитивности.

 В евклидовой геометрии аддитивность углового избытка никак не может быть использована для построения теории площадей: она является просто следствием того обидного с точки зрения наших настоящих интересов обстоятельства, что угловой избыток каждого многоугольника равен в евклидовой геометрии нулю. Однако в неевклидовой геометрии Римана угловой избыток положителен, т. е. удовлетворяет условию а). Таким образом, для того чтобы получить величину, удовлетворяющую всем четырем условиям а) - г), надо лишь нормировать угловой избыток (умножив его на постоянный множитель пропорциональности k) с тем, чтобы соблюдалось и условие г). При этом выбор числа k существенно зависит от выбора единицы измерения площадей. Выберем эту единицу так, чтобы треугольник с тремя прямыми углами (в сферической геометрии отвечающий одной восьмой части полной сферы, см. Рис. 16) имел площадь, равную его угловому избытку, т. е. равную ; при этом площадь всей сферы будет равна 4π (таким образом, радиус сферы принимается здесь за 1), а площадь всей неевклидовой плоскости Римана равна 2π. При этом будем иметь k = 1, т. е. площадь каждого многоугольника будет равна его угловому избытку:

s(M) = ε(M) = A₁ + A₂ + ... + A_n - (n - 2)π.     (8)

В частности, площадь произвольного треугольника ABC будет равна

s_ΔABC = A + B + C - π.     (8a)

Заметим еще, что при таком выборе единицы измерения площадей площадь круга радиуса ρ будет равна

     (9)

(длина прямой в плоскости Римана принимается здесь равной πr).

Выпишем также основные тригонометрические зависимости, связывающие элементы треугольника ABCнеевклидовой геометрии Римана со сторонами AB = c, BC = a, CA = b (в рамках сферической геометрии эти формулы были установлены весьма давно):

     (10)

     (10a)

(теоремы косинусов) и

     (11)

(теорема синусов). [Как и выше, здесь принято, что длина всей прямой в плоскости Римана равна πr.]

     Трехмерная неевклидова геометрия Римана. Совершенно аналогично, отождествляя диаметрально противоположные точки гиперсферы в четырехмерном евкдиловом пространстве, получим трехмерное неевклидово пространство Римана. Если введем в четырехмерном пространстве прямоугольные координаты x,y, z, t, то найдем, что расстояние OM от начала координат до произвольной точки M с координатами x, y, z, tопределяется соотношением

OM² = x² + y² + z² + t².     (12)

Таким образом, если начало координат находится в центре гиперсферы, то ее точки удовлетворяют уравнению

x² + y² + z² + t² = r².     (12a)

     Точки неевклидова пространства Римана можно описать тем же уравнением (12а), если только условиться считать, что M(x, y, z, t) и M₁(-x, -y, -z, -t) - это одна точка.

     Расстояние M₁M₂ между двумя произвольными точками M₁(x₁, y₁, z₁, t₁) и M₂(x₂, y₂, z₂, t₂) четырехмерного пространства определяется по более общей формуле

     (12б)

а угол φ между отрезками OM₁ и OM₂ - по формуле

     (13)

 Если M₁ и M₂ - точки гиперсферы, то расстояние ω между этими точками, измеренное по большой окружности, равно углу между отрезками OM₁ и OM₂, умноженному на радиус r гиперсферы, т. е.

     (14)

а в неевклидовом пространстве Римана, где расстояние ω между точками не может быть больше , это расстояние определяется по формуле

     (14а)

     Будем называть прямой линией и плоскостью в неевклидовом пространстве Римана множество точек этого пространства, получающееся при отождествлении диаметрально противоположных точек, лежащих соответственно на большой окружности и большой сфере гиперсферы. Плоскость неевклидова пространства Римана, очевидно, является неевклидовой плоскостью Римана. Если на гиперсфере у каждой большой сферы имеются два диаметрально противоположных полюса, то в неевклидовом пространстве Римана у каждой плоскости имеется только один полюс. Плоскость можно рассматривать как множество всех точек, отстоящих от полюса на расстоянии πr/2. Так же как в случае прямых на плоскости, показывается, что все перпендикуляры к плоскости в неевклидовом пространстве Римана пересекаются в полюсе этой плоскости (см. Рис. 17) и что всякие две плоскости в этом пространстве обладают общим перпендикуляром, причем каждая точка пересечения плоскостей является полюсом одной из плоскостей, проходящих через этот общий перпендикуляр (см. Рис. 18).

Отсюда вытекает, что при r = 1 угол между двумя плоскостями &945; и β (см. Рис. 19) равен расстоянию между точками A и B их пересечения с их общим перпендикуляром, а также равен расстоянию между полюсами Q и R этих плоскостей.

Последний факт показывает, что плоскости неевклидова пространства Римана находятся во взаимно однозначном соответствии с его точками - полюсами этих плоскостей, причем углы между плоскостями равны расстояниям между соответствующими точками. Таким образом, плоскости неевклидова пространства Римана, если считать углы между ними расстояниями, образуют модель того же пространства; отсюда естественно вытекает, что и в пространственной неевклидовой геометрии Римана имеет место своеобразныйпринцип двойственности. Общий перпендикуляр двух плоскостей и линия их пересечения называютсявзаимными полярами; каждая из этих двух прямых является множеством всех точек, отстоящих одна от другой на расстоянии πr/2; полюс всякой плоскости, проходящей через одну из этих прямых, лежит на другой из них. Отсюда вытекает, что всякий перпендикуляр к прямой пересекается с ее полярой, а общий перпендикуляр двух прямых пересекается с полярами обеих этих прямых. Из свойств двумерных плоскостей четырехмерного пространства следует, что две прямые неевклидова пространства Римана в общем случае обладают двумя общими перпендикулярами, на одном из которых осуществляется максимальное, а на другом - минимальное расстояние между ними; в том же случае, если эти расстояния равны, прямые обладаютбесконечным множеством общих перпендикуляров равной длины. В последнем случае прямые называютсяпаратактичными. Через каждую точку A пространства, не лежащую на прямой a и на ее поляре, можно провести две прямые, паратактичные к данной прямой a (см. Рис. 20): если AP - перпендикуляр, опущенный из точки A на прямую a, b - поляра этого перпендикуляра, пересекающаяся с прямой A в точке Q, а B и C - такие точки прямой b, что расстояния BQ и CQ равны расстоянию ω = AP, то искомые прямые AB и AC; нетрудно видеть, что угол BAC равен углу 2ω/r. Множество всех точек, отстоящих от прямой a на расстоянииρ πr/2, является поверхностью второго порядка, прямолинейные образующие которой паратактичны прямойa и ее поляре a' (см. Рис. 21); каждая пара прямолинейных образующих разных семейств пересекается под одним и тем же углом 2ω/r.

Замечательным свойством этой поверхности, открытой английским геометром В. К. Клиффордом, является то, что на ней господствует евклидова геометрия: поверхность Клиффорда изометрична евклидову ромбу с острым углом 2ω/r и стороной πr, у которого отождествлены точки противоположных сторон, соединяемые прямыми, параллельными другим сторонам (см. Рис. 22).