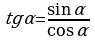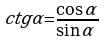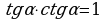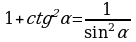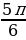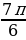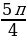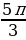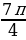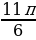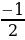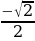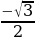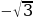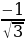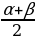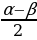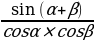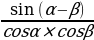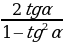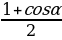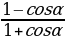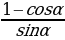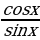ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
"ВОЛГОГРАДСКИЙ КОЛЛЕДЖ МАШИНОСТРОЕНИЯ И СВЯЗИ"
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
ПО ДИСЦИПЛИНЕ ОУДП.04 МАТЕМАТИКА
ПО РАЗДЕЛУ «ОСНОВЫ ТРИГОНОМЕТРИИ»
Волгоград – 2023 год
| Рассмотрено на заседании ЦК Протокол № от Председатель ЦК /______________/ | Одобрено МС Протокол № от Председатель МС /____________/ |
Автор-разработчик: Стороженко Евгения Дмитриевна – преподаватель.
Краткая аннотация: Настоящие методические указания разработаны для проведения практических работ по дисциплине ОУДП.04 Математика по теме «Основы тригонометрии». Каждая практическая работа содержит теоретическую справку, примеры решений заданий и задания для выполнения самостоятельной практической работы обучающихся.
СОДЕРЖАНИЕ
| Пояснительная записка | 4 |
| Практическая работа №1 | 6 |
| Практическая работа №2 | 8 |
| Практическая работа №3 | 12 |
| Практическая работа №4 | 15 |
| Практическая работа №5 | 17 |
| Практическая работа №6 | 21 |
| Практическая работа №7 | 23 |
| Практическая работа №8 | 25 |
| Заключение | 29 |
| Список рекомендуемой литературы | 30 |
Пояснительная записка
Дисциплина «Математика» входит в состав общих общеобразовательных учебных дисциплин, формируемых из обязательных предметных областей ФГОС среднего общего образования, для профессий СПО или специальностей СПО соответствующего профиля профессионального образования, и играет ведущую роль в общей и профессиональной системах образования студентов среднего профессионального образования.
Раздел «Основы тригонометрии», включенный в содержание учебной дисциплины и отраженный в практических заданиях данного методического указания, является общим для всех профилей профессионального образования.
Тригонометрия – раздел математики, в котором изучаются тригонометрические функции, их свойства, а также тригонометрические тождества и преобразования тригонометрических выражений, решение тригонометрических уравнений и неравенств. Тригонометрические вычисления применяются практически во всех областях математики, физики и других учебных дисциплинах.
Целью данного пособия является помощь обучающимся в организации их практической работы по разделу дисциплины «Основы тригонометрии».
Методическое указание содержит все структурные элементы для организации и проведения самостоятельных практических работ.
При работе с методическими указаниями рекомендуется вначале изучить имеющуюся краткую теоретическую часть. При выполнении практической работы следует руководствоваться следующими указаниями:
Практическую работу выполняют в отдельной тетради школьного формата в клетку.
Работу выполняют чернилами одного цвета, аккуратно, разборчиво.
Каждую практическую работу выполняют с новой страницы.
Каждую решенную задачу (упражнение) необходимо сопровождать ответом.
Чертежи следует выполнять карандашом с использованием чертежных инструментов, аккуратно, соблюдая масштаб.
Решения задач должны сопровождаться краткими, но обоснованными пояснениями, используемые формулы нужно выписывать.
Данное указание содержит восемь тем:
Применение радианного метода измерения углов вращения и связь с градусной мерой;
Применение основных тригонометрических тождеств, формул приведения и сложения;
Решение простейших задач на использование основных формул тригонометрии;
Преобразование тригонометрических выражений;
Построение графиков тригонометрических функций;
Решение тригонометрических уравнений;
Решение тригонометрических неравенств;
Решение тригонометрических уравнений и систем.
Все темы содержат:
Справочный теоретический материал.
Примеры с решением.
Задания для самостоятельной практической работы.
Практическая работа №1
Тема: Применение радианного метода измерения углов вращения и связь с градусной мерой
Цель практической работы: получить навыки применения формул перехода от градусной меры к радианной и наоборот.
Справочный теоретический материал
Градус (обозначение °) – единица измерения углов равная 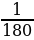 развернутого угла.
развернутого угла.
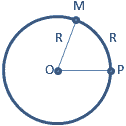 Радиан – единица измерения углов, равная величине центрального угла, которому соответствует длина дуги, равная длине радиуса окружности (рис 1).
Радиан – единица измерения углов, равная величине центрального угла, которому соответствует длина дуги, равная длине радиуса окружности (рис 1).
Рис. 1
![]()
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит α радиан, то его градусная мера равна:
![]()
И наоборот:
![]()
Обычно при обозначении меры угла в радианах наименование «рад» опускают. Например, 360° = 2π рад, пишут 360° = 2π
При радианном измерении углов упрощается ряд формул. Так, для окружности радиуса r длины l ее дуги в α радиан находится по формуле:
l=αr
А площадь S сектора круга радиуса r, дуга которого содержит α радиан находится по формуле:
S = 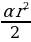
Примеры с решением
Пример 1. Выразите в радианах величину угла α, если 1) α=30̊, 2)α=135̊.
Решение: Так как ![]() , то :
, то :
30̊ =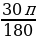 =
= 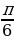
135̊ = 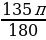 =
= 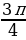
Ответ: 1)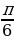 ; 2)
; 2)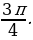
Пример 2. Выразите в градусной мере величину угла α , если 1) α=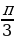 , 2) α=
, 2) α= 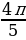 .
.
Решение: Так как ![]() , то:
, то:
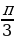 =
= 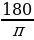 ×
× 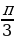 = 60̊
= 60̊
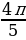 =
= 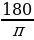 ×
× 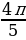 = 144̊
= 144̊
Ответ: 1) 60̊ ; 2) 144̊.
Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера 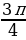 .
.
Решение: Найдем длину дуги окружности, используя формулу l=αr:
l=6×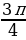 = 4,5π (см)
= 4,5π (см)
Ответ: 4,5π (см)
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла 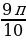 .
.
Решение: Воспользуемся формулой для нахождения площади сектора S = 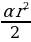 :
:
S = 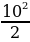 ×
×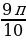 =
= 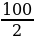 ×
×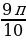 = 45π
= 45π
Ответ: 45π
Задания для практической работы
Задание №1. Найти радианную меру угла, градусная мера которого равна:
а) 15̊, 200̊, 45̊, 216̊, 330̊;
б) 25̊, 100̊, 60̊, 72̊, 270̊.
Задание №2. Найти градусную меру угла, радианная мера которого равна:
а) 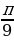 ;
;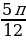 ;
; 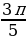 ;
; 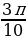 ; π;
; π;
б) 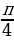 ;
; 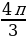 ;
; 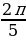 ;
; 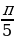 ;
; 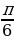
Задание №3. Найдите радианную меру угла, который соответствует дуге окружности длиной 4см, если радиус окружности равен 1,5 см.
Задание №4. Найдите площадь кругового сегмента, если радиус окружности 12 см, а угол равен α= 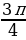 .
.
Задание №5. Найдите радианную меру угла смежного с углом 60̊.
Задание №6. Контрольные вопросы:
Что такое угол в 1 радиан?
Запишите формулу перехода от радианной меры угла к градусной.
Запишите формулу перехода от градусной меры угла к радианной.
Практическая работа №2
Тема: Применение основных тригонометрических тождеств, формул приведения и сложения.
Цель практической работы: закрепить умение применять основные тригонометрические тождества, таблицу значений тригонометрических функций при упрощении и вычислении выражений.
Справочный теоретический материал
Основные тригонометрические тождества
Тригонометрические функции связаны между собой следующими основными тождествами:
| 1. 2. 3. | 4. 5. 6. |
Значения тригонометрических функций некоторых углов приведены в следующей таблице:
| α | 0 | | | | | | | | π | | | | | | | | 2π |
| 0̊ | 30̊ | 45̊ | 60̊ | 90̊ | 120̊ | 135̊ | 150̊ | 180̊ | 210̊ | 225̊ | 240̊ | 270̊ | 300̊ | 315̊ | 330̊ | 360̊ | |
| sin α | 0 | | | | 1 | | | | 0 | | | | -1 | | | | 0 |
| cos α | 1 | | | | 0 | | | | -1 | | | | 0 | | | | 1 |
| tg α | 0 | | 1 | | - | | -1 | | 0 | | 1 | | - | | -1 | | 0 |
| ctg α | - | | 1 | | 0 | | -1 | | - | | 1 | | 0 | | -1 | | - |
Знаки тригонометрических функций в различных четвертях
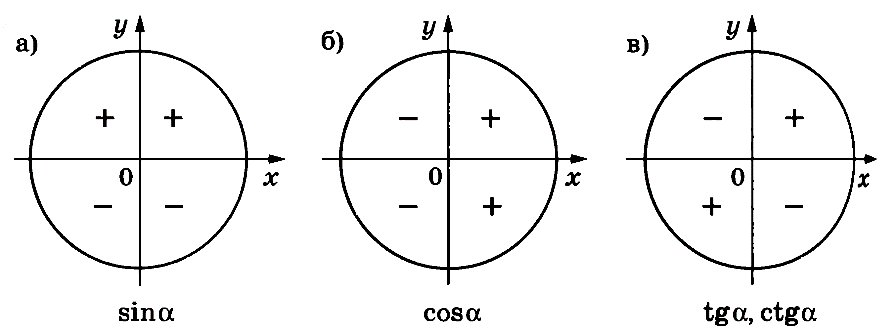
Рисунок 2
Знаки тригонометрических функций определяются в зависимости от того, в какой четверти лежит рассматриваемый угол. I четверть – от 0̊ до 90̊, II четверть – от 90̊ до 180̊, III четверть– от 180̊ до 270̊, IV четверть – от 270̊ до 360̊.
Формулы сложения:
cos (α-β)=cosα cosβ + sinα sinβ
cos (α+β)=cosα cosβ - sinα sinβ
sin (α-β)=sinα cosβ + cosα sinβ
sin (α+β)=sinα cosβ + cosα sinβ
tg (α+β) = 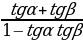
tg (α-β) = 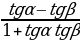
С помощью формул приведения осуществляется преобразование выражений вида: sin (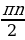 ±α), cos (
±α), cos (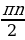 ±α), tg (
±α), tg (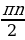 ±α), ctg (
±α), ctg (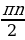 ±α), n ∈ Z.
±α), n ∈ Z.
Правило для записи формул приведения:
перед приведённой функцией ставится тот знак, который имеет исходная функция (рис.2), если 0˂α˂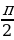 ;
;
функция меняется на «кофункцию», если n нечётно; функция не меняется, если n чётно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.).
Примеры с решением
Пример 1. Определите знак cos 52̊.
Решение: Угол 52̊ - угол первой четверти, значит cos 52̊ имеет знак +.
Ответ: знак +.
Пример 2. Упростить выражение: 1 – sin2α.
Решение: Для решения воспользуемся основным тригонометрическим тождеством: 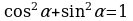 =˃
=˃
1 – sin2α = cos2α + sin2α – sin2α = cos2α
Ответ: cos2α
Пример 3. Найдите значение tgα, если cosα = 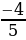 ,
, 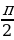 ˂ α˂ π.
˂ α˂ π.
Решение: Для решения воспользуемся одной из формул тригонометрического тождества: 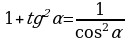 =˃
=˃
tg2α = 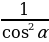 – 1 =
– 1 = 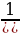 -1 =
-1 = 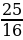 -1=
-1= 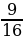
Получаем: tgα =± 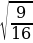 = ±
= ±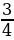 . Знак тангенса определяем по углу α. Известно, что
. Знак тангенса определяем по углу α. Известно, что 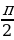 ˂ α˂ π. Очевидно, это II четверть, где все тангенсы отрицательны. Поэтому tgα=
˂ α˂ π. Очевидно, это II четверть, где все тангенсы отрицательны. Поэтому tgα= 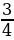 .
.
Ответ:- 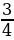 .
.
Пример 4. С помощью формул сложения, вычислить cos15̊.
Решение: Представим 15̊ в виде разности 45̊-30̊ и воспользуемся формулой сложения cos (α-β)=cosα cosβ + sinα sinβ. Получаем,
cos15̊ = cos(45̊-30̊) = cos45̊×cos30̊ + sin45̊×sin30̊ =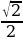 ×
×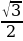 +
+ 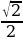 ×
×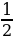 =
= 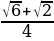 .
.
Ответ: 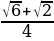 .
.
Пример 5. Используя формулы приведения, найдите значение sin150̊.
Решение: Обратим внимание, что 150̊ мы можем представить в виде (90̊+60̊). Теперь применим к синусу формулу приведения:
90̊+60̊ – это I четверть, синус в ней положителен. Значит знак будет плюс
90̊ - находится на «вертикали» - функция меняется на кофункцию. Получаем,
sin150̊= sin(90̊+60̊) = cos60̊ = 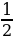
Ответ: 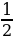
Задания для практической работы
Задание №1. Определите, какой знак имеют sin α, cos α, tg α и ctg α:
а) α = 49̊;
б) α= 128̊.
Задание №2. Упростите выражение:
а) cos2x + (1-sin2x); ctgx - 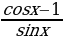 ;
;
б) (1-sinα)×(1+sinα); sin2α + 2cos2α-1.
Задание №3. Найдите значение tgα, если:
а) sinα = -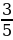 ,
, 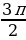 ˂α˂2π;
˂α˂2π;
б) cosα =- 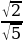 ,
, 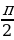 ˂α˂π.
˂α˂π.
Задание №4. Найдите значение выражения:
а) cos107̊×cos17̊ + sin107̊×sin17̊; sin51̊×cos21̊ - cos51̊×sin21̊;
б) cos36̊×cos24̊ - sin36̊×sin24̊; sin63̊×cos27̊ + cos63̊×sin27̊.
Задание №5. Используя формулы привидения, вычислите:
а) cos (-210̊);
б) sin (-150̊)
Задание №6. Контрольные вопросы:
1) В каком случае функция не изменяется?
2) Как определяется знак функции?
3) Какие формулы можно вывести из основного тригонометрического тождества?
Практическая работа №3
Тема: Решение простейших задач на использование основных формул тригонометрии
Цель практической работы: закрепить умения применять основные формулы тригонометрии.
Справочный теоретический материал
Формулы суммы и разности тригонометрических функций:
| sinα + sinβ = 2sin sinα - sinβ = 2sin cosα + cosβ = 2cos | cosα - cosβ = -2sin tgα + tgβ = tgα - tgβ = |
Формулы двойного аргумента:
| sin2α= 2sinα cosα; cos2α = cos2α-sin2α; tg2a = | cos2α = 1 - 2sin2α; cos2α = 2cos2α – 1. |
Формулы половинного аргумента:
| sin2 cos2 | tg2 tg |
| tg | |
Примеры с решением
Пример 1. Упростите выражение 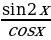 .
.
 Решение: Преобразуем числитель по формуле двойного аргумента:
Решение: Преобразуем числитель по формуле двойного аргумента:
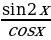 =
= 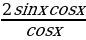 = 2sinx
= 2sinx
Ответ: 2sinx
Пример 2. Вычислите 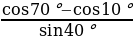 .
.
Решение: Преобразуем числитель по формуле разности косинусов, а знаменатель оставим прежним:
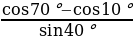 =
= 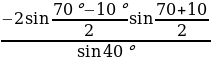 =
= 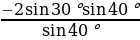 = -2sin30̊ = -2
= -2sin30̊ = -2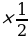 = -1
= -1
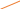 Ответ: -1
Ответ: -1
Пример 3. Вычислите sin2α и cos2α, если sinα = -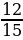 и π˂α˂
и π˂α˂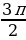 .
.
Решение: Используя основное тригонометрическое тождество, найдем cosα
cos2α=1-sin2α = 1-(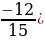 2 = 1
2 = 1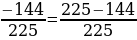 =
= 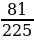
Так как π˂α˂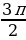 , то угол α – угол III четверти, значит cosα имеет знак минус, получаем: cosα =
, то угол α – угол III четверти, значит cosα имеет знак минус, получаем: cosα = 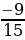 .
.
По формулам двойного угла найдем sin2α и cos2α:
sin2α = 2×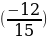 ×(
×(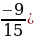 =
= 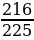
cos2α = (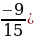 2 – (-
2 – (-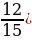 2 =
2 = 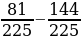 = -
= -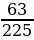 .
.
Ответ: sin2α =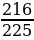 ; cos2α =-
; cos2α =-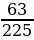 .
.
Пример 4. Найдите sin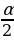 , если cosα = -
, если cosα = -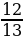 , π˂α˂
, π˂α˂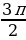 .
.
Решение: Так как π˂α˂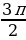 (третья четверть), то разделим обе части этого неравенства на 2, при этом знаки неравенства останутся прежними:
(третья четверть), то разделим обе части этого неравенства на 2, при этом знаки неравенства останутся прежними: 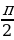 ˂
˂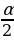 ˂
˂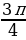 (вторая четверть).
(вторая четверть).
Значит sin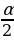 ˃ 0.
˃ 0.
Воспользуемся формулой половинного аргумента:
sin2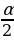 =
= 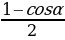 =
= 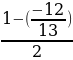 =
= 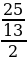 =
= 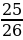 .
.
sin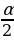 =
= 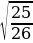 =
= 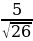 =
= 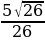 .
.
Ответ: 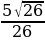
Задания для практической работы
Задание №1. Упростите выражения:
а) cos2x+sin2x;
б) 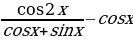 .
.
Задание №2. Вычислите:
а) 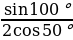 ; 2sin
; 2sin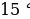 ×cos
×cos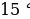 ;
;
б) 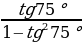 ;
; 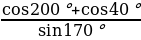 .
.
Задание №3. Вычислите sin2α и cos2α, если sinα = -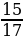 и
и 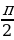 ˂α˂π
˂α˂π
Задание №4. Вычислите tg2α, если tgα= 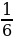
Задание №5. Найдите sin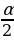 , cos
, cos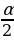 , tg
, tg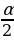 , если cosα =
, если cosα = 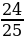 ,
, 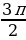 .˂α˂2π.
.˂α˂2π.
Задание №6. Контрольные вопросы
1) Чему равна сумма и разность синусов и косинусов?
2) Какими формулами пользовались при вычислении?
Практическая работа №4
Тема: Преобразование тригонометрических выражений
Цель практической работы: закрепить навыки применения тригонометрических формул при вычислении значений тригонометрических функций и преобразовании выражений, содержащих тригонометрические функции.
Справочный теоретический материал
Преобразование тригонометрических выражений – это упрощение выражений, которое выполняется с помощью тригонометрических формул
Основные формулы
| sin2x + cos2x = 1 tgx = ctgx = | 1+tg2x = 1+ctg2x = tgx × ctgx = 1 |
Примеры с решением
Пример 1. Докажите тождество: (1+tgα)2 + (1-tgα)2 = 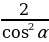
Решение: Для доказательства упростим левую часть равенства и покажем, что она всегда равна правой. Используя формулы суммы и разности квадратов, запишем выражение в развернутом виде:
(1+tgα)2 + (1-tgα)2 = 1+2tgα + tg2α + 1-2tgα + tg2α
Сократим противоположные слагаемые и приведем подобные:
 1+2tgα + tg2α + 1-2tgα + tg2α = 1+ tg2α + 1+ tg2α = 2+2 tg2α
1+2tgα + tg2α + 1-2tgα + tg2α = 1+ tg2α + 1+ tg2α = 2+2 tg2α
Вынесем за скобки общий множитель 2:
2+2 tg2α = 2(1+ tg2α)
Заметим, что 1+ tg2α = 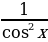 . Получаем:
. Получаем:
2(1+ tg2α) = 2×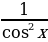 =
= 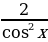
Видим, что после упрощения левая часть равенства тождественно равна правой.
Доказано.
Пример 2. Упростите тригонометрическое выражение: 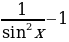 .
.
Решение: Заметим, что 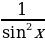 = 1+ctg2x. Получаем:
= 1+ctg2x. Получаем:
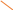
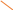
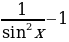 = 1+ctg2x – 1 = ctg2x.
= 1+ctg2x – 1 = ctg2x.
Ответ: ctg2x.
Пример 3. Докажите, что при всех допустимых значениях α, значение выражение
не зависит от α: 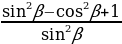 .
.
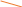
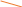 Решение: Преобразуем числитель. Заменим 1, используя основное тригономтерическое тождество:
Решение: Преобразуем числитель. Заменим 1, используя основное тригономтерическое тождество:
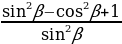 =
=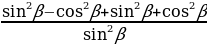 =
= 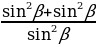 =
= 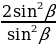 = 2
= 2
Получили выражение, не зависящее от α.
Задания для практической работы
Задание №1. Докажите тождество:
а) (tgα + ctgα)2 -(tgα - ctgα)2; 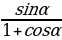 +
+ 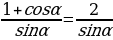 ;
;
б) 1-tg2β = 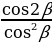 ;
; 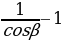 = tg2β.
= tg2β.
Задание №2. Упростите выражения:
а) tg2x + sin2x - 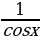 ; sin2x + cos2x+tg2x; (sinx + 2cosx)2-4sinx×cosx;
; sin2x + cos2x+tg2x; (sinx + 2cosx)2-4sinx×cosx;
б) tg2x(1-sin2x) ; 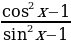 + tg
+ tg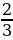 ctg
ctg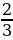 ; ctgx -
; ctgx - 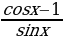 .
.
Задание №3. Докажите, что при всех допустимых значениях α, значение выражение не зависит от α:
а) 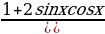 ;
;
б) 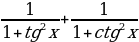 .
.
Задание №4. Контрольные вопросы:
1) Какими формулами пользовались при решении данных примеров?
Практическая работа №5
Тема: Построение графиков тригонометрических функций
Цель практической работы: закрепить навыки построения графиков тригонометрических функций.
Справочный теоретический материал
Функцией называется зависимость переменной y от переменной x ,при которой каждому x ставится в соответствие единственное значение y.
При этом x называется независимой переменной (аргументом), а y – зависимой переменной (функцией).
Обозначается функция: y=f(x).
Областью определения функции D(f) называется множество всех значений переменной x, при которых данная функция имеет смысл.
Областью значений функции Е(f) называется множество, состоящее из всех чисел f(x), таких, что x принадлежит области определения функции f.
Графиком функции f называют множество всех точек (х,у) координатной плоскости, где y=f(x), а x «пробегает» всю область определения функции f.
Функцию f называют чётной, если для любого x из области определения функции выполняется равенство: f(-х)= f(х).
Функцию f называют нечётной, если для любого x из области определения функции выполняется равенство: f(-х)= - f(х).
Функция синус
Числовая функция, заданная формулой y=sinx , называется функцией синус.
Область определения функции синус – множество всех действительных чисел, т.е. D(y)=R.
Областью значений функции синус является отрезок [-1;1], т.е. E(y) = [-1;1].
Синус – нечётная функция, т.е. для любого числа x выполняется равенство sin(-x) = - sin x
Синус периодическая функция с пределом Т=2π, т.е. для любого x выполняется равенство sin(x+2πn) = sin x, где n – произвольное целое число.
График синуса называется синусоидой (рис.3).
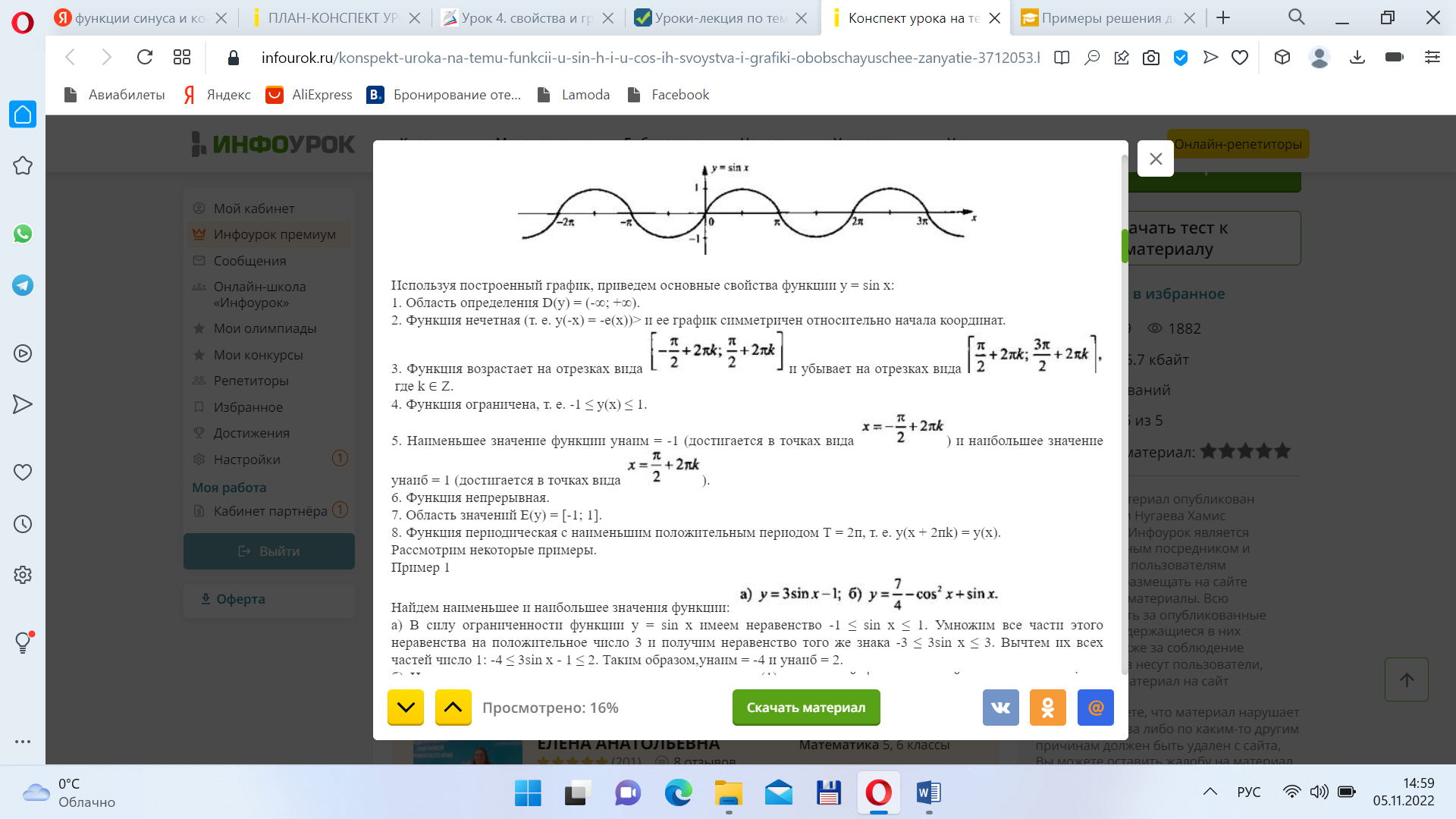
Рисунок 3
Функция косинус
Числовая функция, заданная формулой y=cosx , называется функцией косинус.
Область определения функции косинус – множество всех действительных чисел, т.е. D(y) = R.
Областью значений функции косинус является отрезок [-1;1], т.е. E(y)=[-1;1] .
Косинус чётная функция, т.е. для любого x выполняется равенство cos (-x) = cos x.
Косинус периодическая функция с периодом T= 2π, т.е. для любого x выполняется равенство cos(x+2πn)=cos x, где n – произвольное целое число.
График косинуса называется косинусоида. (рис. 4).
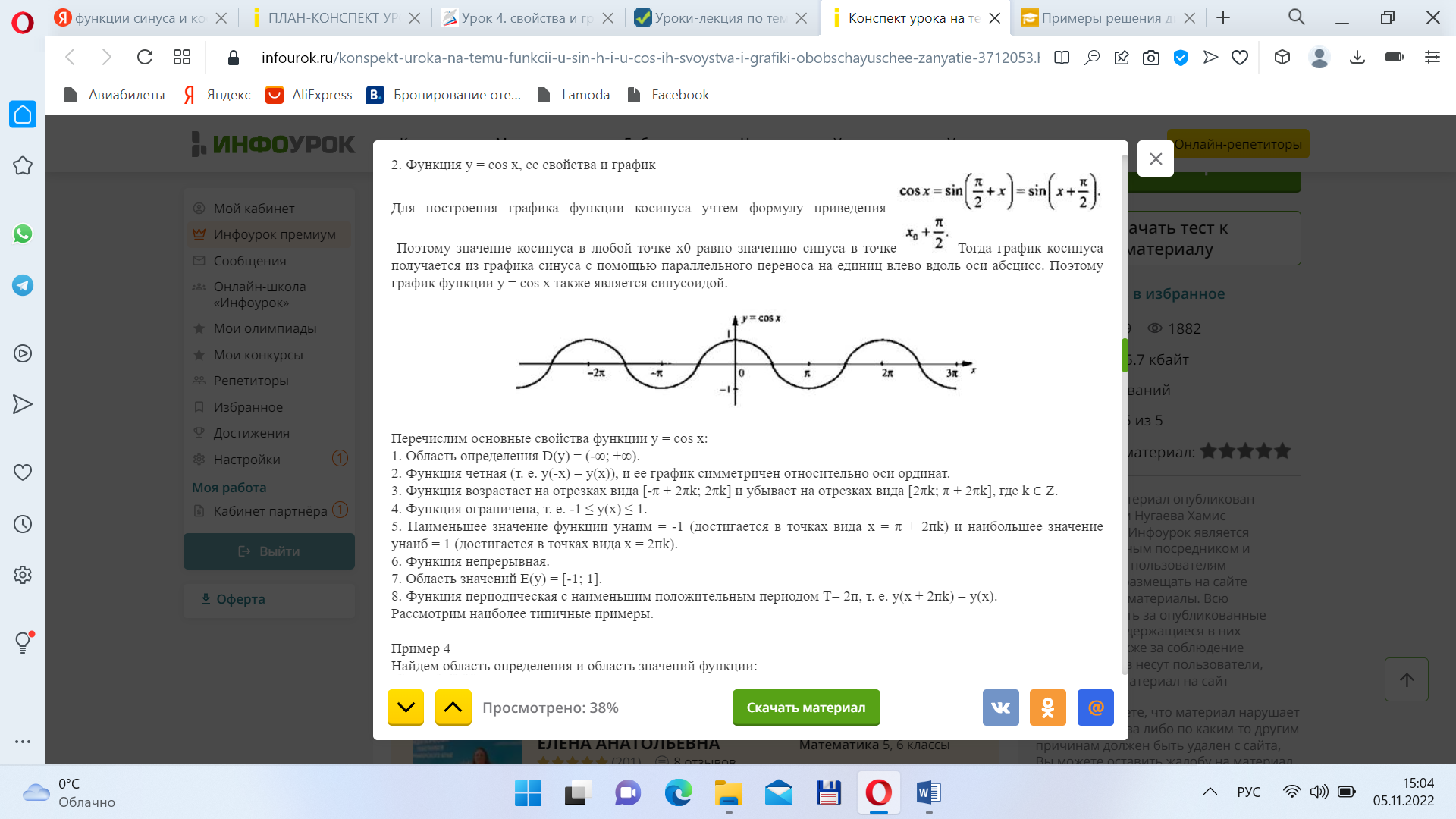
Рисунок 4
Функция тангенс
Числовая функция, заданная формулой y = tg x, называется функцией тангенс.
Область определения функции y = tgx все действительные числа, кроме чисел вида x=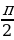 +πn, n
+πn, n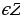
Область значения тангенса – все действительные числа, т.е. E(y) = R
Тангенс является нечётной функцией, т.е. для любого x выполняется равенство tg(-x) = -tg x.
Тангенс периодическая функция с периодом Т = π, т.е. для любого x выполняется равенство tg(x + πn) = tg x, n є Z.
График тангенса называется тангенсоида. (рис.5)
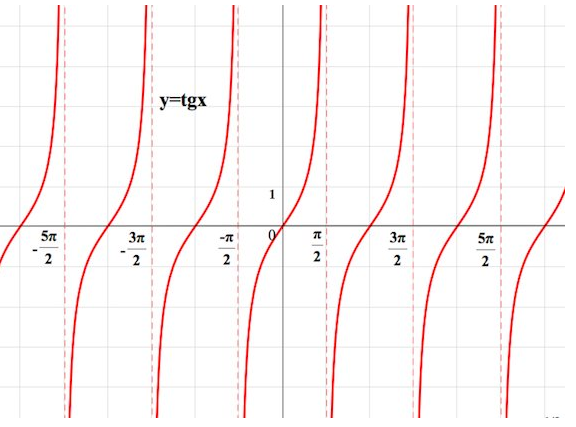
Рисунок 5
Функция котангенс
Числовая функция, заданная формулой y =ctgx, называется функцией котангенс.
Область определения функции котангенс – множество всех чисел x, для которых sin x ≠ 0, т.е. D(y) = (πn; π + πn), где n є Z.
Область значений котангенса – все действительные числа, т.е. E(y) R.
Котангенс является нечётной функцией, т.е. для любого x выполняется равенство ctg(-x) = -ctg x.
Котангенс периодическая функция с периодом Т = π, т.е. для любого x выполняется равенство ctg(x + πn) = ctg x, где n є Z.
График котангенса называют котангенсоидой. (рис.6)
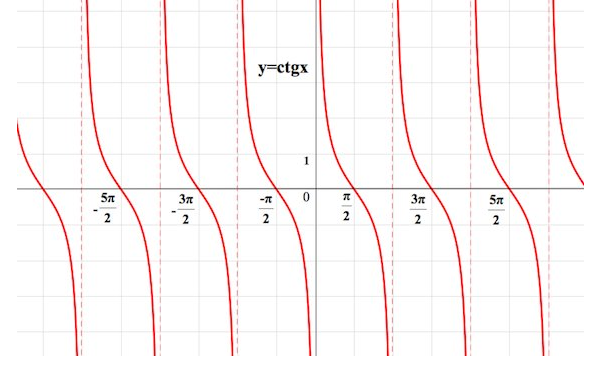
Рисунок 6
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: f (kx b) , при этом k 0,b 0 .
Функцию f(kx b) необходимо представить в виде f(kx b) = f(k(x+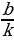 ) и последовательно выполнить следующие преобразования:
) и последовательно выполнить следующие преобразования:
1) График функции f (x) сжимаем (или растягиваем) к оси (от оси) ординат: f (kx).
2) График полученной функции f (kx) сдвигаем влево (или вправо) вдоль оси абсцисс на 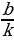 единиц, в результате чего будет построен искомый график f (kx b).
единиц, в результате чего будет построен искомый график f (kx b).
Примеры с решением
Пример 1. Построить график функции y sin 2x.
Решение: Сначала строим график y sin x . Период T 2 .
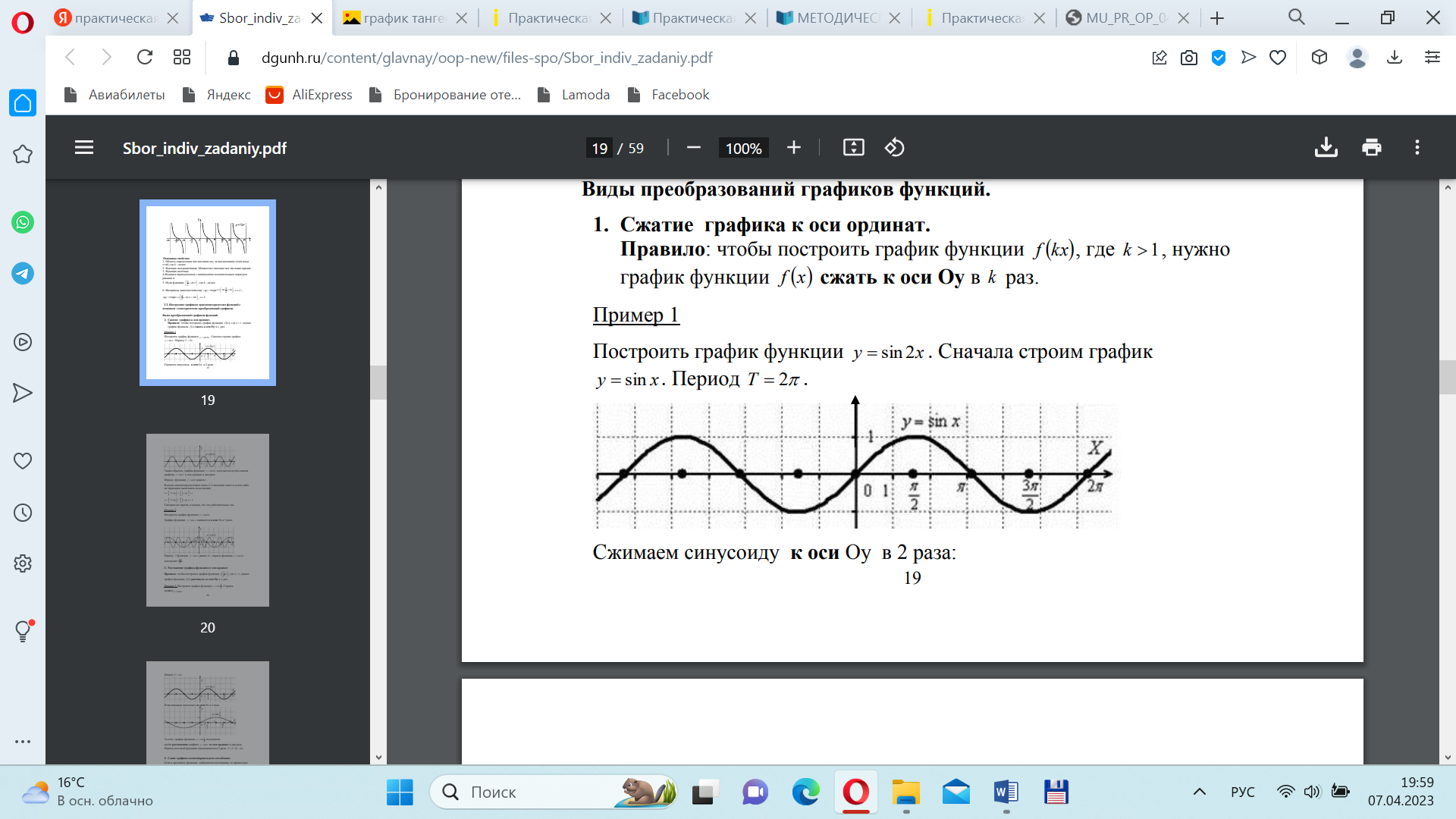
Сжимаем синусоиду к оси Оу в 2 раза:
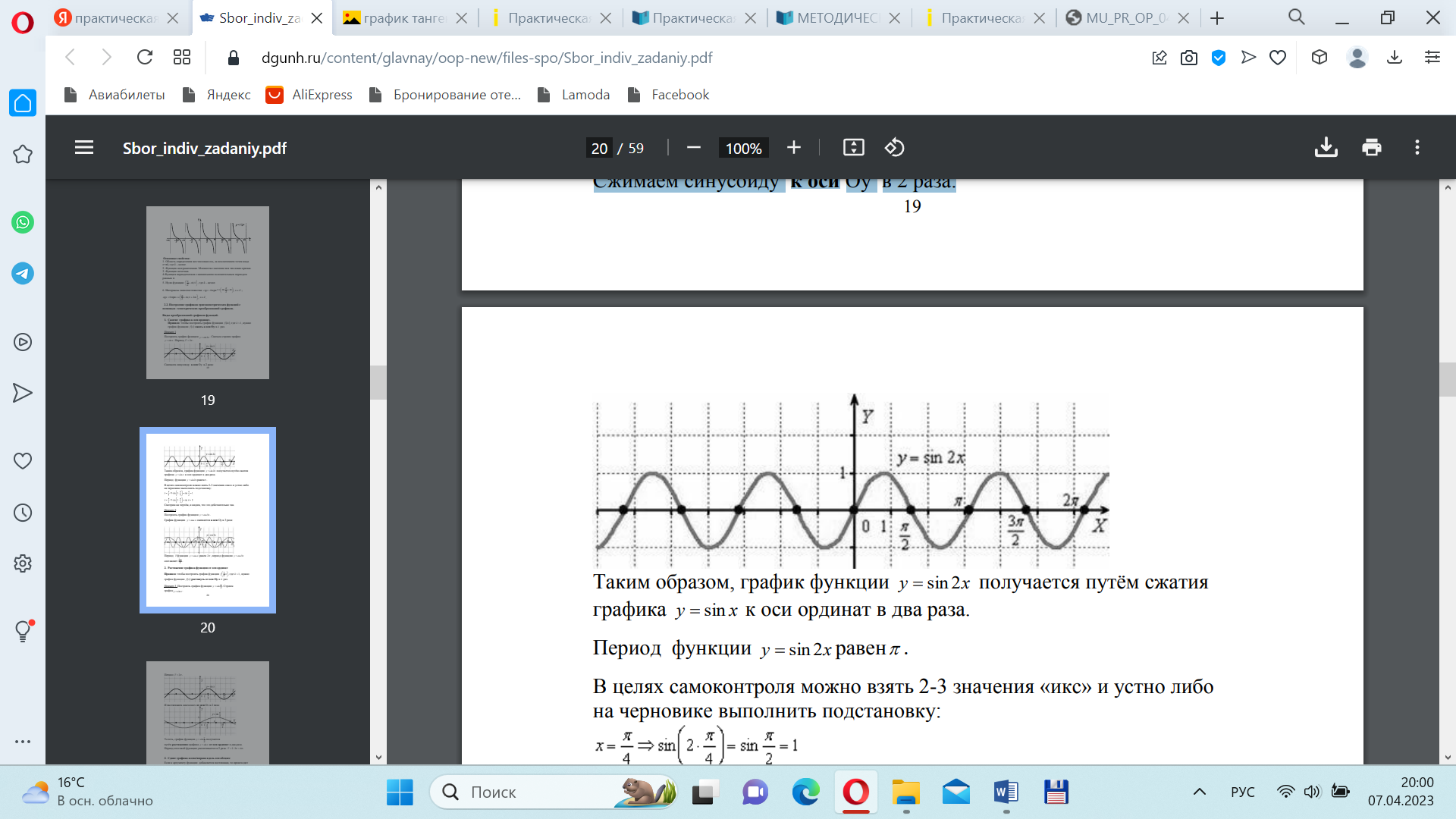
Таким образом, график функции y sin 2x получается путём сжатия графика y sinx к оси ординат в два раза.
Период функции y sin2x равен .
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
x = 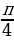 =˃ sin(2×
=˃ sin(2×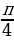 ) = sin
) = sin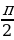 = 1
= 1
x = 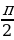 =˃ sin(2×
=˃ sin(2×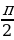 ) = sinπ = 0
) = sinπ = 0
Смотрим на чертёж, и видим, что это действительно так.
Пример 2. Построить график функции y=sin(2x+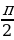 )
)
Решение: 1)Представим функцию в виде y=sin(2(x+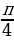 )) и выполним следующие преобразования: синусоиду y sin x сожмём к оси Оу в два раза: y sin 2x .
)) и выполним следующие преобразования: синусоиду y sin x сожмём к оси Оу в два раза: y sin 2x .
2) сдвинем вдоль оси Ох на 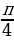 влево:
влево:
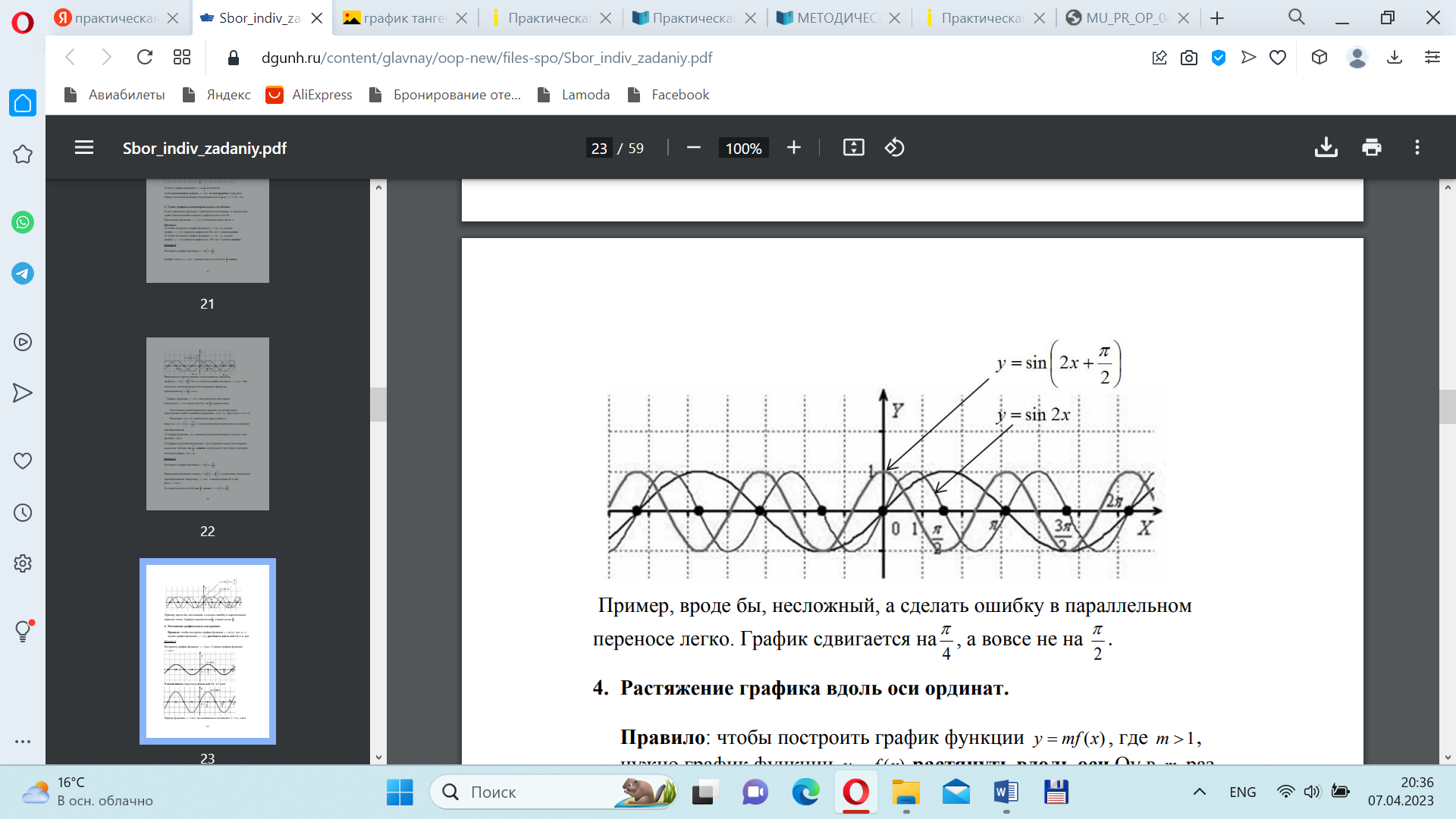
Задания для практической работы
Задание №1. Построить график функции y cos3x .
Задание №2. Построить график функции y = cos (2x + 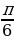 ).
).
Задание №3. Построить график функции y = sin (3x - 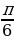 ).
).
Задание №4. Контрольные вопросы:
1) Напишите свойства тригонометрических функций.
Практическая работа №6
Тема: Решение тригонометрических уравнений
Цель практической работы: Закрепить навыки решения тригонометрических уравнений.
Справочный теоретический материал
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрической функции.
Простейшие уравнения
1) Уравнение вида sinx=α.
Уравнение sinx=a может иметь решение только при |α|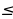 1.Известно, что решение этого уравнения находят по обобщенной формуле:
1.Известно, что решение этого уравнения находят по обобщенной формуле:
x=(-1)narcsinα +πn, где n Z и -
Z и - .
.
Частные случаи:
Если sinx=1, то x=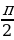 +2πn, n
+2πn, n Z.
Z.
Если sinx=-1, то x=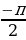 +2πn, n
+2πn, n Z.
Z.
Если sinx=0, то x=πn, n Z.
Z.
2) Уравнение вида cosx=α.
Уравнение cosx=α может иметь решение только при |α|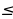 1. Известно, что решение данного уравнения находят по обобщенной формуле:
1. Известно, что решение данного уравнения находят по обобщенной формуле:
x=±arccosα +2πn, где n Z и 0
Z и 0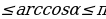 .
.
Полезно знать, что arccos(-α) = π – arccosα.
Частные случаи:
Если cosx=0, то x=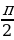 +πn, n
+πn, n Z.
Z.
Если cosx=1, то x=2πn, n Z.
Z.
Если cosx=-1, то x=π+2πn, n Z.
Z.
3) Уравнение вида tgx=α, где α=R
Известно, что решение заданного уравнения находят по обобщенной формуле:
x=arctgα+πn, где n Z.
Z.
Полезно помнить, что arctg(-α)= -arctgα
4) Уравнение вида сtgx=α, где α=R
Известно, что решение заданного уравнения находят по обобщенной формуле:
X=arcсtgα+πn, где n Z.
Z.
Примеры с решением
Пример 1. Решить уравнение: sinx = 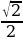 .
.
Решение: Воспользуемся формулой x=(-1)narcsinα +πn, подставляем:
x=(-1)narcsin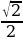 +πn, n
+πn, n Z.
Z.
Так как аrcsin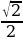 =
= 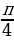 , то получаем:
, то получаем:
x=(-1)n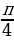 +πn, n
+πn, n Z.
Z.
Ответ: x=(-1)n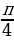 +πn, n
+πn, n Z.
Z.
Пример 2. Решить уравнение: 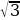 tgx – 1=0.
tgx – 1=0.
Решение: Перенесем 1 из левой части в правую и поменяем знак на противоположный:
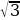 tgx =1.
tgx =1.
Разделим каждую часть на 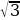 :
:
tgx = 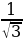 .
.
Воспользуемся формулой x=arctgα+πn:
x=arctg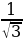 +πn, где n
+πn, где n Z.
Z.
Так как arctg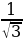 =
= 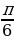 , то получаем:
, то получаем:
x= 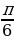 +πn, где n
+πn, где n Z.
Z.
Ответ: x= 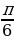 +πn, где n
+πn, где n Z.
Z.
Пример 3. Решить уравнение: 2sin(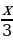 +
+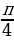 )=
)= 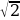 .
.
Решение: Разделим данное уравнение на 2, получим:
sin(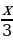 +
+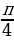 )=
)= 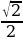 .
.
Воспользуемся формулой x=(-1)narcsinα +πn, подставляем:
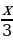 +
+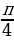 =(-1)narcsin
=(-1)narcsin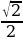 +πn, n
+πn, n Z.
Z.
Так как аrcsin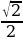 =
= 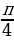 , то получаем:
, то получаем:
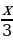 +
+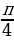 =(-1)n
=(-1)n 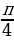 +πn, n
+πn, n Z.
Z.
Перенесем вправо:
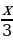 =(-1)n
=(-1)n 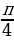 -
-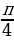 +πn, n
+πn, n Z.
Z.
Умножим обе части равенства на 3:
х = =(-1)n 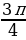 -
-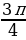 +πn, n
+πn, n Z.
Z.
Ответ: х = =(-1)n 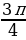 -
-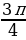 +πn, n
+πn, n Z.
Z.
Задания для практической работы
Задание №1. Решить уравнения: cosx = -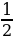 ; tgx=
; tgx=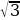 ; ctgx =
; ctgx = 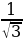 ; cosx=-
; cosx=-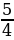 ; sinx =
; sinx = 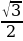 .
.
Задание №2. Решить уравнения: 2sinx-1=0; 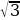 ctgx-1=0; 2cosx+
ctgx-1=0; 2cosx+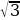 =0.
=0.
Задание №3. Решить уравнения: 2sin(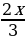 +
+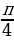 ) = 1; 2cos(
) = 1; 2cos( 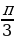 -5x) =
-5x) = 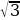 /
/
Задание №4. Контрольные вопросы:
1) Какие методы знаете для решения простейших тригонометрических уравнений?
Практическая работа №7
Тема: Решение тригонометрических неравенств
Цель практической работы: Закрепить навыки решения тригонометрических неравенств.
Справочный теоретический материал
Неравенства, содержащие переменную под знаком тригонометрической функции, называются тригонометрическими.
При решении тригонометрических неравенств используют единичную окружность.
Примеры с решением
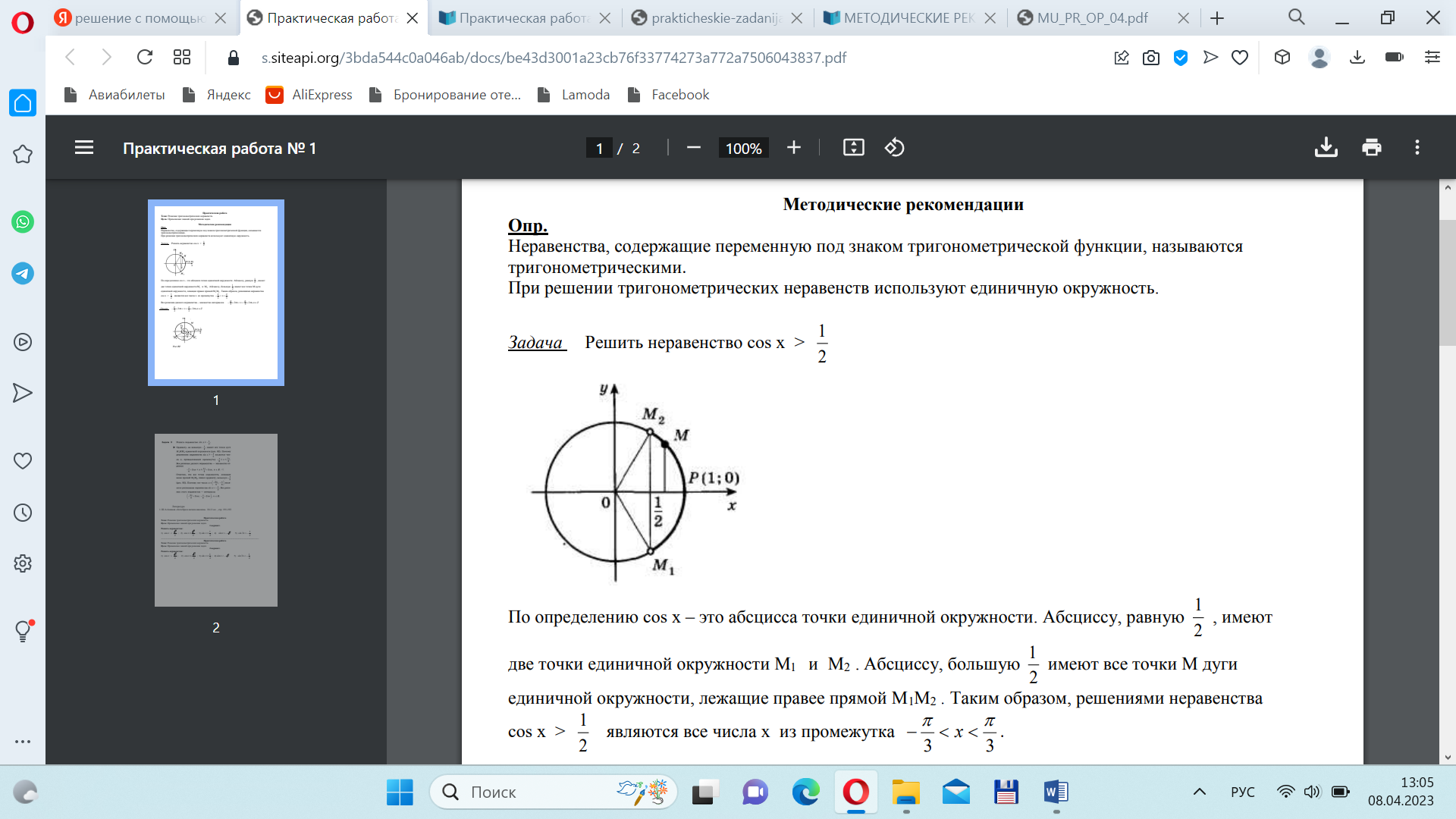 Пример 1. Решить неравенство: cos x
Пример 1. Решить неравенство: cos x 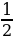 .
.
Рисунок 7
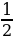 , имеют две точки единичной окружности М1 и М2.(рис.7) Абсциссу, большую
, имеют две точки единичной окружности М1 и М2.(рис.7) Абсциссу, большую 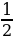 имеют все точки М дуги единичной окружности, лежащие правее прямой М1М2. Таким образом, решениями неравенства cosx
имеют все точки М дуги единичной окружности, лежащие правее прямой М1М2. Таким образом, решениями неравенства cosx 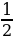 являются все числа х из промежутка -
являются все числа х из промежутка - 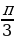 x
x 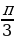 .
.
Все решения данного неравенства – множество интервалов - 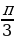 + 2πn x
+ 2πn x 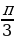 +2πn, n
+2πn, n Z.
Z.
Ответ: - 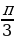 + 2πn x
+ 2πn x 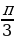 +2πn, n
+2πn, n Z.
Z.
Пример 2. Решить неравенство: cos2x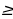 -
-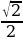 .
.
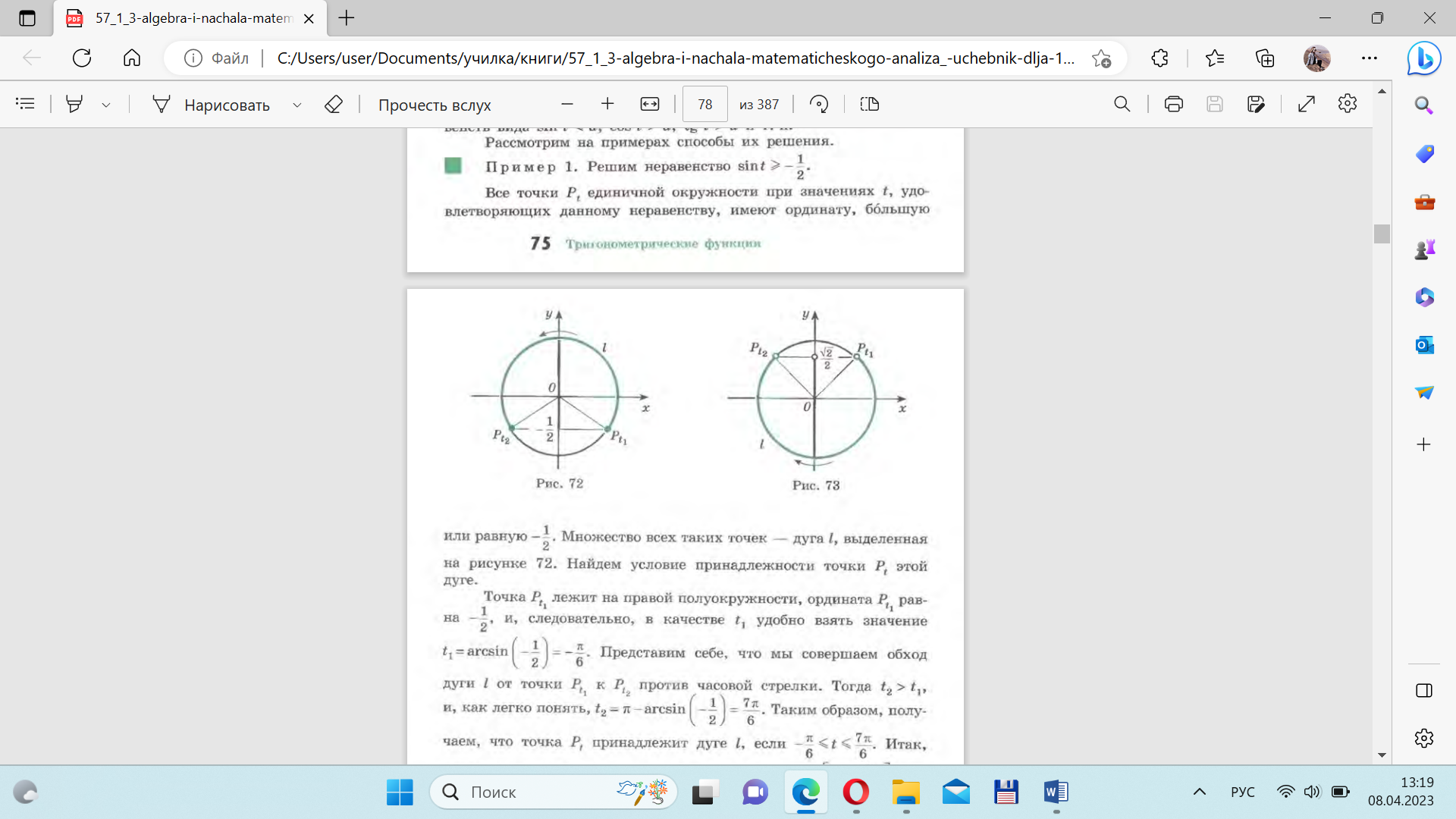 Решение: Обозначив 2х через t, получим cost
Решение: Обозначив 2х через t, получим cost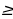 -
-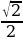 . На рис.8 выделена соответствующая дуга l. Находим t1=arccos (-
. На рис.8 выделена соответствующая дуга l. Находим t1=arccos (-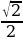 ) =
) = 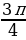 , t2=-
, t2=-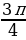 , откуда
, откуда
- 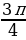 + 2πn t
+ 2πn t 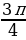 +2πn, n
+2πn, n Z.
Z.
Рисунок 8
- 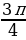 + 2πn 2x
+ 2πn 2x 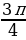 +2πn, -
+2πn, - 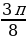 + πn x
+ πn x 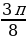 +πn, n
+πn, n Z.
Z.
Ответ: - 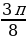 + πn x
+ πn x 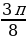 +πn, n
+πn, n Z
Z
Задания для практической работы
Задание №1. Решить неравенства:
а) sinx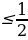 ; tgx
; tgx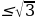 ; cosx
; cosx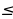 -1;
-1;
б) sinx 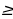 1; sinx
1; sinx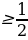 ; tgx
; tgx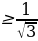 .
.
Задание №2. Решить неравенства:
а) ctg3x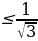 ; sin2x ˂
; sin2x ˂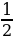 ; cos2x˂-
; cos2x˂-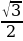 ;
;
б) cos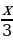 ˃
˃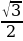 ; sin
; sin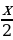 ˂-
˂-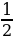 ; sin3x˂-
; sin3x˂-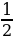 .
.
Задание №3. Контрольные вопросы:
1) Какие неравенства называются тригонометрическими?
2) Что используют при решении тригонометрических неравенств?
Практическая работа №8
Тема: Решение тригонометрических уравнений и систем
Цель практической работы: проверить и закрепить знания по решению тригонометрических уравнений и систем уравнений с применением тригонометрических формул.
Справочный теоретический материал
Более сложные тригонометрические уравнения обычно решаются сведением их к простейшим с помощью различных алгебраических и тригонометрических формул и преобразований.
Виды тригонометрических уравнений:
а) уравнения, алгебраические относительно одной из тригонометрических функций;
б) уравнения, решаемые понижением их порядка;
в) уравнения, решаемые после преобразований с помощью тригонометрических формул;
г) однородные уравнения.
Простейшие системы уравнений: к ним отнесем системы, в которых или одно из уравнений является линейным, или уравнения системы могут быть решены независимо друг от друга.
Системы, решаемые с помощью замены неизвестных: если система содержит только две тригонометрические функции или приводится к такому виду, то удобно использовать замену неизвестных.
Примеры с решением
Пример 1. Решить уравнение: 2sin2x + sinx – 1=0.
Решение: Это уравнение является квадратным относительно sinx. Введем новую переменную у= sinx. Тогда данное уравнение можно записать в виде:
2у2+у-1=0.
Мы получили квадратное уравнение. Найдем корни этого уравнения:
2у2+у-1=0.
D=b2-4ac = 12-4×2×(-1) = 9; 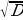 =3.
=3.
y = 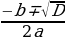
y1= 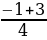 =
= 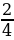 =
= 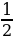
y2= 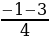 =
= 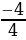 = -1
= -1
Получаем: sinx= 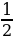 или sinx=-1. В первом случае получим решения:
или sinx=-1. В первом случае получим решения:
x=(-1)narcsin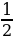 +πn, n
+πn, n Z,
Z,
т.е. x=(-1)n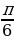 +πn, n
+πn, n Z.
Z.
Во втором случаем имеем:
x=-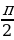 +2πn, n
+2πn, n Z.
Z.
Ответ: (-1)n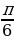 +πn, n
+πn, n Z, где n
Z, где n Z; -
Z; -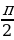 +2πn, n
+2πn, n Z.
Z.
Пример 2. Решить уравнение: 6sin2x + 5cosx – 2=0.
Решение: Так как квадрат синуса легко выражается через косинус, то, заменяя sin2x на 1 – cos2х и приводя уравнение к квадратному относительно cosx, получим:
6(1-cos2x) +5cosx - 2=0,
т.е. квадратное уравнение: -6cos2x +5cosx + 4 = 0 =˃ 6cos2x -5cosx - 4 =0
Введем новую переменную у= cosx. Тогда данное уравнение можно записать в виде:
6y2-5y-4=0
Найдем корни уравнения:
D = (-5)2-4×6×(-4) = 121; 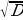 =11
=11
y1 = 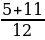 = 1
= 1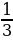 ;
;
y1 = 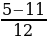 = -
= -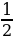 .
.
Получаем: cosx=1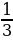 и cosx= -
и cosx= -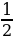 .
.
cosx=1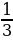 – не имеет решений, так как 1
– не имеет решений, так как 1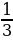 ˃1;
˃1;
Решая уравнение cosx= -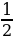 , находим:
, находим:
х = ±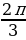 + 2πn, n
+ 2πn, n Z.
Z.
Ответ: ±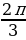 + 2πn, n
+ 2πn, n Z.
Z.
Пример 3. Решить уравнение: sin2x – 5sinxcosx + 6cos2x = 0.
Решение: Если считать, что sinx и cosx – члены первой степени, то каждое слагаемое имеет вторую степень. Уравнение, в котором каждое слагаемое имеет одну и ту же степен, называется однородным. Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2x. (При этом мы не теряем корней, так как если мы в данное уравнение подставим cosx=0, то получим, что и sinx=0, что невозможно.)
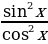 - 5
- 5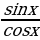 +6
+6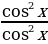 = 0
= 0
tg2x – 5tgx +6 = 0
Введем новую переменную у= tgx. Тогда данное уравнение можно записать в виде:
y2-5y+6 = 0
Найдем корни уравнения:
D = (-5)2-4×1×6 = 1; 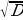 =1
=1
y1 = 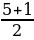 = 3;
= 3;
y1 = 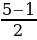 = 2.
= 2.
Получаем: tgx=3 и tgx=2. В первом случае получим решение:
х = arctg3+πn, n Z.
Z.
Во втором случаем имеем:
х = arctg2+πn, n Z.
Z.
Ответ: arctg3+πn, n Z; arctg2+πn, n
Z; arctg2+πn, n Z.
Z.
Пример 4. Решить систему уравнений: 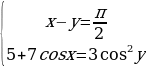
Решение: Так как первое уравнение является линейным, то выразим из него переменную x= 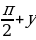 и подставим во второе уравнение:
и подставим во второе уравнение:
5+7cos ( 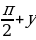 )= 3cos2y.
)= 3cos2y.
Используем формулу приведения и основное тригонометрическое тождество. Получим уравнение: 5 – 7siny = 3(1-sin2y) или 3sin2y – 7siny +2=0.
Введем новую переменную t = siny. Тогда данное уравнение можно записать в виде:
3t2-7t +2=0
Найдем корни уравнения:
D = (-7)2-4×3×2 = 25; 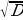 =5
=5
t1 = 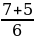 = 2;
= 2;
t1 = 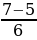 =
= 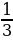 .
.
Вернемся к старой неизвестной и получим уравнения:
siny = 2 - не имеет решений, так как 2˃1;
siny =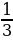
y=(-1)narcsin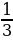 +πn, n
+πn, n Z.
Z.
Теперь легко найти неизвестную:
x= 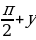 =
= 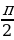 + (-1)narcsin
+ (-1)narcsin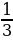 +πn.
+πn.
Итак, система уравнений имеет решения: ( 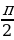 + (-1)narcsin
+ (-1)narcsin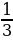 +πn; (-1)narcsin
+πn; (-1)narcsin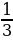 +πn), где n
+πn), где n Z.
Z.
Пример 5. Решить систему уравнений: 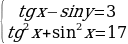
Решение: Так как в данную систему входят только две тригонометрические функции, то введем новые переменные а = tg х и b = sin у. Получим систему алгебраических уравнений: 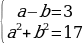 .
.
Из первого уравнения выразим а = b + 3 и подставим во второе: (b+3)2 +b2 =17 или b2+3b-4=0.
Корни этого квадратного уравнения b1 = 1 и b2= -4. Соответствующие значения а1 = 4 и а2 = -1. Вернемся к старым неизвестным. Получим две системы простейших тригонометрических уравнений:
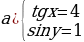 , ее решение х = arctg4+πn, y=
, ее решение х = arctg4+πn, y=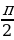 + 2πn, n
+ 2πn, n Z.
Z.
б) 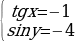 , решений не имеет, так как siny˃-1.
, решений не имеет, так как siny˃-1.
Ответ: х = arctg4+πn, y=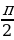 + 2πn, n
+ 2πn, n Z
Z
Задания для практической работы
Задание №1. Решить уравнение: 3sin2x – 5sinx – 2=0.
Задание №2. Решить уравнение: cos2x +3sinx = 3.
Задание №3. Решить уравнение: 9sinxcosx – 7cos2x = 2sin2x.
Задание №4. Решить систему уравнений: 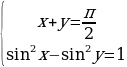 .
.
Задание №5. Решить систему уравнений: 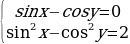 .
.
Задание №6. Контрольные вопросы:
1) Каковы особенности решения систем тригонометрических уравнений?
Заключение
Данные практические работы позволяют формировать знания и умения необходимые в профессиональной деятельности.
В результате самостоятельного поэтапного решения предложенных заданий, обучающиеся получают достаточно полное представление о практическом использовании изученного теоретического материала.
Критерии оценки
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна существенная ошибка или два-три несущественных ошибки.
Отметка «3» ставится, если:
допущены более одной существенной ошибки или более двух-трех несущественных ошибок, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет 63 обязательными умениями по данной теме в полной мере.
К категории существенных ошибок следует отнести ошибки, связанные с незнанием, непониманием учащимися основных положений теории и с неправильным применением методов, способов, приемов решения практических заданий, предусмотренных программой.
К категории несущественных ошибок следует отнести погрешности, связанные с небрежным выполнением записей, рисунков, графиков, чертежей, а также погрешности и недочеты, которые не приводят к искажению смысла задания и его выполнения. При наличии существенной ошибки задание считается невыполненным.
Список рекомендуемой литературы
Алимов Ш. А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2017.
Башмаков, М.И. Алгебра и начала анализа. 10 кл. [Текст]: учебник / М.И. Башмаков – М.: Дрофа, 2008.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2018.
Интернет-ресурсы:
1. Www.fcior.edu.ru (информационные, тренировочные и контрольные материалы).
2. Www.school-collection.edu.ru (единая коллекции цифровых образовательных ресурсов).