Конические Сечения

Кони́ческое сече́ние или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых. Окружность можно рассматривать как частный случай эллипса.
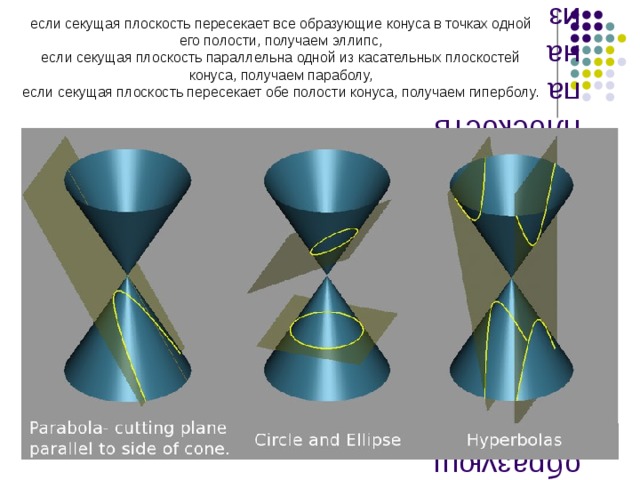
- если секущая плоскость пересекает все образующие конуса в точках одной его полости, получаем эллипс, если секущая плоскость параллельна одной из касательных плоскостей конуса, получаем параболу, если секущая плоскость пересекает обе полости конуса, получаем гиперболу.
если секущая плоскость пересекает все образующие конуса в точках одной его полости, получаем эллипс,
если секущая плоскость параллельна одной из касательных плоскостей конуса, получаем параболу,
если секущая плоскость пересекает обе полости конуса, получаем гиперболу.

Декартовы координаты
В декартовых координатах, конические сечения описываются общим квадратным многочленом:
Иначе говоря, конические сечения являются кривыми второго порядка. Знак дискриминанта
определяет тип конического сечения.
Если дискриминант меньше нуля, то это эллипс, точка или пустое множество.
Если дискриминант равен нулю, то это парабола, прямая или пара параллельных прямых.
Если дискриминант больше нуля, то это гипербола или пара пересекающихся прямых

- Свойство: Через любые пять точек на плоскости, никакие три из которых не лежат на одной прямой, можно провести единственное коническое сечение.
- История: Конические сечения были известны ещё математикам Древней Греции. Наиболее полным сочинением, посвящённым этим кривым, были «Конические сечения» Аполлония Пергского (около 200 г. до н. э.).





