Ключевые задачи по геометрии для 7 класса

Ключевые задачи по геометрии для учащихся 7 класса.

ЗАДАЧА 1

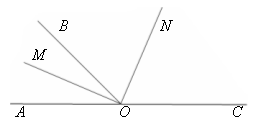
Угол, образованный биссектрисами двух смежных углов, равен 90. Доказать.

Дано: АОВ и ВОС – смежные. ОМ – биссектриса АОВ. ON – биссектриса ВОС. Доказать: MON = 90.

Доказательство

MON = MOB + BON = АОВ + ВОС = ( АОВ + ВОС) = АОC = 180 = 90. MON = 90что и требовалось доказать.

ЗАДАЧА 2

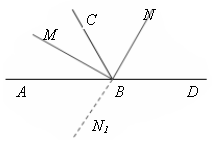
Докажите, что если биссектрисы углов ABC и CBD перпендикулярны, то точки A, B, D лежат на одной прямой. (Задача 85.)

Дано: ABC и CBD. BM –биссектриса ABC. BN –биссектриса NBD. BN  BM. Доказать: точки A, B, D лежат на одной прямой.

Доказательство

Заметим, что луч BN₁ (продолжение луча BN) не может быть биссектрисой CBD, иначе CBD 180. (Но CBD .) По условию BN BM, т. е. MBN = 90. МВС + CBN = 90.

2 (МВС + CBN) = 2 · 90°.

2 · МBС + 2 · CBN = 180, ABC + CBD = 180.

ABD = 180, отсюда точки A, B, D лежат на одной прямой, ч. т. д.

ЗАДАЧА 3

Биссектрисы вертикальных углов лежат на одной прямой. Доказать.

Дано: АОВ и А₁ОВ₁ – вертикальные.

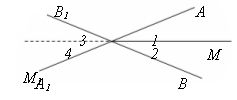
Доказать: биссектрисы вертикальных углов лежат на одной прямой.

Доказательство

Пусть ОМ – биссектриса АОВ : 1 = 2.

Продолжим луч ОМ, получим луч ОМ₁.

Докажем, что 3 = 4 (Замена на аналогичную задачу.)

Луч ОМ₁ проходит внутри А₁ОВ₁, 1 и 4, 2 и 3 – вертикальные, поэтому

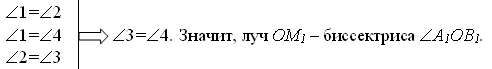
Т. о., биссектрисы ОМ и ОМ₁ вертикальных углов АОВ и А₁ОВ₁ лежат на одной прямой ММ₁, что и требовалось доказать.

ЗАДАЧА 4

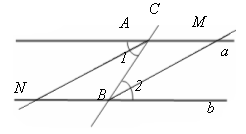
Две параллельные прямые пересечены секущей. Докажите, что биссектрисы накрест лежащих углов параллельны.

Дано: а || b, с  а, с  b. 1 и 2 накрест лежащие. АN – биссектриса 1. ВМ – биссектриса 2. Доказать: АN || ВМ.

Доказательство

1. а || b, поэтому 1=2.

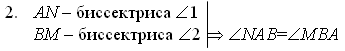
Так как половины равных углов равны, то...

NАВ и МВА – накрест лежащие.

4. АN || ВМ, ч. т. д.

ЗАДАЧА 5

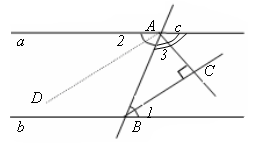
Две параллельные прямые пересечены секущей. Докажите, что биссектрисы односторонних углов перпендикулярны.

Дано: а || b, с  а, с  b. 1 и 3 односторонние. АС – биссектриса 3. ВС – биссектриса 1. Доказать: АС  ВС.

Доказательство

1. Проведем биссектрису АD угла 2.

1. а || b, 1 и 2 – накрест лежащие, значит, их биссектрисы параллельны: АD || ВС (опорная задача 4).

2. 2 и 3 – смежные, поэтому их биссектрисы перпендикулярны: АD  АС (опорная задача 1).

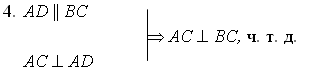
ЗАДАЧА 6

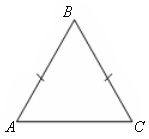
Если один из углов равнобедренного треугольника равен 60, то этот треугольник равносторонний. Доказать.

	1) Дано: ∆АВС АВ=ВС А=60	2) Дано: ∆АВС АВ=ВС В=60
	Доказать: ∆АВС – равносторонний.

Доказательство

1. ∆АВС – равнобедренный с основанием АС, поэтому А = С = 60. А + В + С = 180, отсюда В = 180– 60= 180– 120= 60. Так как А = В = С, то ВС = АС = АВ, т. е. ∆АВС – равносторонний, ч. т. д.

1. ∆АВС – равнобедренный с основанием АС, поэтому А = С. А + В + С = 180, отсюда А = 180– 60= 120, А = 120, А = = 60. Итак, А = В = С,  ВС = АС = АВ, т. е. ∆АВС – равносторонний, ч. т. д.

ЗАДАЧА 7

Прямые АВ и CD параллельны, АС – секущая. С помощью циркуля и линейки постройте биссектрису угла ACD.

Дано: АВ || CD, АС – секущая.

Построить: биссектрису ACD.

Анализ

Пусть СМ – биссектриса ACD, тогда 1 = 2. АВ || CD, 2 и 3 – накрест лежащие, значит, 2 = 3. Получаем 1 = 2 = 3. В ∆АСМ углы при основании равны, поэтому АС = АМ.

Построение

Измеряем циркулем отрезок АС и на луче АВ откладываем АМ = АС. Проводим луч СМ.

Луч СМ – искомый.

Доказательство

В ∆АСМ АС = АМ, поэтому 1 = 3. АВ || CD, поэтому 2 = 3 как накрест лежащие. Таким образом, 1 = 2, значит, СМ – биссектриса ACD.

Исследование

Задача имеет единственное решение.

ЗАДАЧА 8

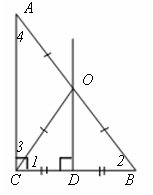
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. Доказать.

Дано: ∆АВС – прямоугольный. С = 90°, СО – медиана. Доказать: СО = АВ.

Доказательство

1. Проведем через середину D отрезка СВ прямую DE  СВ (О = DEАВ).

1. ∆COD = ∆BOD по двум катетам, поэтому СО = ВО и 1 = 2.

2. 1 + 3 = 2 + 4 = 90

3. 3 = 4, значит, в ∆АОС : АО = СО.

4. Получаем СО = АО = ВО = АВ, ч. т. д.

Справедливо обратное утверждение:

Если в треугольнике одна из медиан равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

Дано: ∆АВС, СО − медиана, СО = АВ.

Доказать: АВС − прямоугольный (С = 90°).

Доказательство

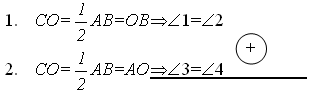
1 + 3 = 2 + 4 1 + 3 = (1 + 3 + 2 + 4) =

= (А + В + С) = · 180= 90.

1 + 3 = С = 90, значит, ∆АВС – прямоугольный, ч. т. д.

ЗАДАЧА 9

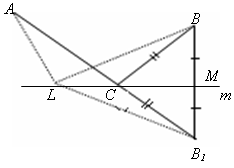
Два населенных пункта А и В находятся по одну сторону от прямой дороги. Где на дороге надо расположить автобусную остановку С, чтобы сумма расстояний АС + СВ была наименьшей?

Дано: m, Аm, Вm. Точки А и В расположены по одну сторону от прямой m. Найти: точку Сm, чтобы АС + СВ было наименьшим.

Построение

1. Из точки В проведем прямую ВВ₁  m (М = ВВ₁  m) и отложим МВ₁ = МВ.

1. _{Построим отрезок} АВ_1.

2. С=АВ₁m.

Точка С – искомая.

Доказательство

1. Прямоугольные ∆СМВ и ∆СМВ₁ равны по двум катетам: СМ – общая, МВ = МВ₁ по построению, значит, СВ = СВ₁.

1. АВ₁ = АС + СВ₁ = АС + СВ.

2. Пусть L – любая точка прямой m, отличная от С. Применяя неравенство треугольника для ∆АLВ₁, имеем: АВ₁ АL + LВ₁, т. е. АС + СВ₁ АL + LВ₁, АС + СВ АL + LВ. Таким образом, сумма расстояний АС + В будет наименьшей, ч. т. д.

ЗАДАЧА 10

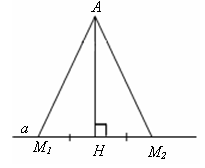
Из точки А к прямой а проведены перпендикуляр АН и наклонные АМ₁ и АМ₂.

_{Докажите, что если} НМ₁ = НМ₂, то АМ₁ = АМ_2.

Дано: АН  а, НМ1 = НМ2 Доказать: АМ1 = АМ2.

Доказательство

Треугольники АНМ₁ и АНМ₂ равны по двум катетам, поэтому АМ₁ = АМ₂, ч. т. д.

ЗАДАЧА 11

Из точки А к прямой а проведены перпендикуляр АН и наклонные АМ₁ и АМ₂.

_{Докажите, что если} НМ₁ НМ₂, то АМ₁ АМ_2.

Дано: АН  а, НМ1 НМ2. Доказать: АМ1 АМ2.

Доказательство

1. Отложим НМ'₁ = НМ₁, проведем АМ'₁.

1. НМ₁ = НМ'₁ и АН  а, значит, АМ₁ = АМ'₁ и 1 = 3.

2. 3 – внешний в ∆АМ'₁М₂, поэтому 3 2, а значит, и 1 2.

3. В ∆АМ₁М₂ 1 2, поэтому АМ₂ АМ₁, или АМ₁ АМ₂, ч. т. д.