Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
Определение четырёхугольника. Виды четырёхугольников.
Доказать теорему Фалеса.
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
В треугольнике АВС
 =90
=90 ,sinА=
,sinА=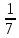 , АС=4
, АС=4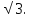 Найдите АВ.
Найдите АВ.
Билет №2.
Параллелограмм. Определение. Свойства параллелограмма.
Доказать теорему о средней линии треугольника.
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
В треугольнике АВС
 =90
=90 ,sinА=
,sinА=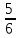 , АС=5
, АС=5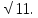 Найдите АВ.
Найдите АВ.
Билет №3.
Квадрат. Определение. Свойства.
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
В треугольнике АВС
 =90
=90 ,АВ=182, АС=70. Найдите tgА.
,АВ=182, АС=70. Найдите tgА.
Билет №4.
Пропорциональность отрезков в прямоугольном треугольнике.
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
В треугольнике АВС
 =90
=90 ,ВС=28, АВ=35. Найдите sinВ.
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
Ромб. Доказательство теоремы о диагоналях ромба.
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
В треугольнике АВС
 =90
=90 ,cosВ=
,cosВ=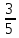 , АВ=5
, АВ=5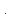 Найдите АС.
Найдите АС.
Билет № 6.
Касательная к окружности. Свойства.
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
В треугольнике АВС
 =90
=90 ,cosВ=
,cosВ=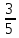 , АВ=45
, АВ=45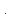 Найдите АС.
Найдите АС.
Билет № 7.
Площадь четырехугольников: параллелограмма, трапеции
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
В треугольнике АВС
 =90
=90 ,ВС=
,ВС=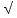 21, АВ=5. Найдите sinВ.
21, АВ=5. Найдите sinВ.
Билет №8.
Вписанная и описанная окружности в треугольники и четырехугольники.
Докажите свойство противолежащих сторон и углов параллелограмма.
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
В треугольнике АВС
 =90
=90 ,АВ=13, АС=5. Найдите tgА.
,АВ=13, АС=5. Найдите tgА.
Билет №9.
Признаки параллельности прямых.
Докажите теорему об отношении площадей треугольников.
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
В треугольнике АВС
 =90
=90 ,cosВ=
,cosВ=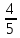 , АВ=25
, АВ=25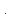 Найдите АС.
Найдите АС.
Билет №10.
Вписанная и описанная окружности в треугольники и четырехугольники.
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
В треугольнике АВС
 =90
=90 ,АВ=15, АС=12. Найдите tgА.
,АВ=15, АС=12. Найдите tgА.
Билет №11.
Вписанный и центральный углы, дуга окружности.
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
В треугольнике АВС
 =90
=90 ,АВ=20, АС=12. Найдите sinА
,АВ=20, АС=12. Найдите sinА
Билет №12.
Признаки равенства треугольников.
Вписанный угол. Докажите теорему о вписанном угле.
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
В треугольнике АВС
 =90
=90 ,sinА=
,sinА=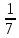 , АС=4
, АС=4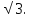 Найдите АВ.
Найдите АВ.
Билет № 13.
Понятие площади многоугольника. Свойства площадей.
Докажите теорему Пифагора.
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
В треугольнике АВС
 =90
=90 ,sinА=
,sinА=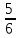 , АС=5
, АС=5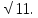 Найдите АВ.
Найдите АВ.
Билет №14.
Формулы для вычисления площади параллелограмма.
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
В треугольнике АВС
 =90
=90 ,АВ=182, АС=70. Найдите tgА.
,АВ=182, АС=70. Найдите tgА.
Билет №15.
Признаки равенства прямоугольных треугольников.
Вписанный угол. Докажите теорему о вписанном угле.
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
В треугольнике АВС
 =90
=90 ,ВС=28, АВ=35. Найдите sinВ.
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
Треугольник. Свойства равнобедренного треугольника.
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
В треугольнике АВС
 =90
=90 ,cosВ=
,cosВ=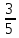 , АВ=5
, АВ=5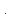 Найдите АС.
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.

 =90
=90 ,
,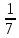 , АС=4
, АС=4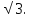 Найдите АВ.
Найдите АВ.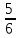 , АС=5
, АС=5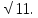 Найдите АВ.
Найдите АВ.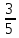 , АВ=5
, АВ=5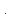 Найдите АС.
Найдите АС.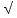 21, АВ=5. Найдите
21, АВ=5. Найдите 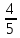 , АВ=25
, АВ=25



