ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ
ТРЕУГОЛЬНИКА
Геометрия
8 класс
Сахарова Наталия Ивановна
МБОУ СОШ №28 г.Симферополя

- Точка пересечения медиан треугольника
- Точка пересечения биссектрис треугольника
- Точка пересечения высот треугольника
- Точка пересечения срединных перпендикуляров треугольника
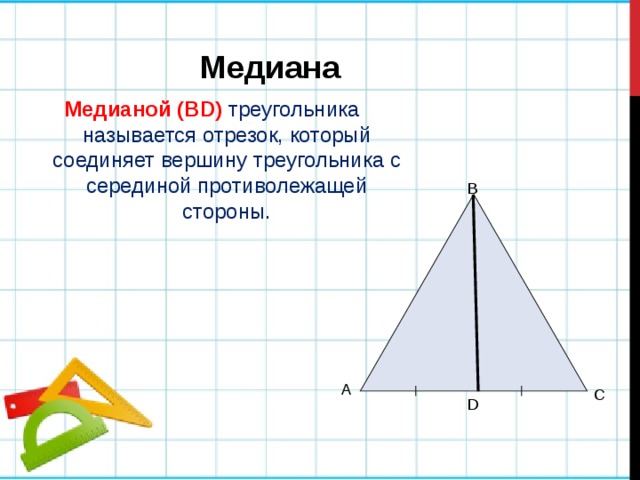
Медиана
Медианой (BD) треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
В
А
С
D
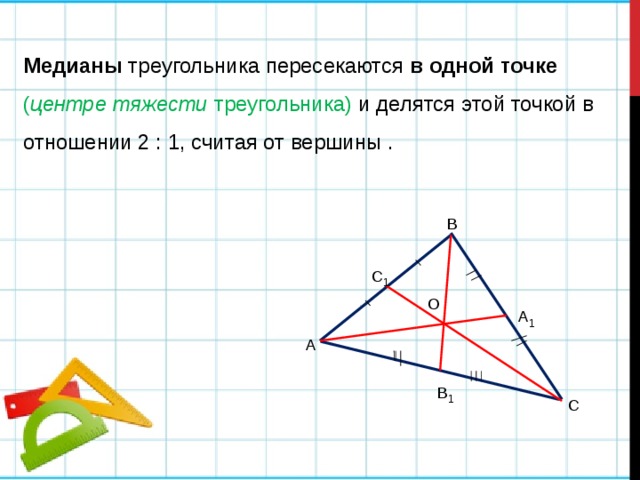
Медианы треугольника пересекаются в одной точке ( центре тяжести треугольника) и делятся этой точкой в отношении 2 : 1, считая от вершины .
В
С 1
О
А 1
А
В 1
С
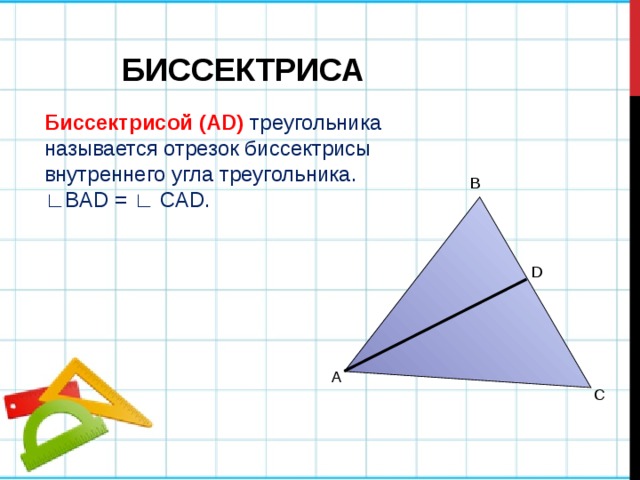
БИССЕКТРИСА
Биссектрисой (АD) треугольника называется отрезок биссектрисы внутреннего угла треугольника. ∟ BAD = ∟ CAD.
В
D
A
C
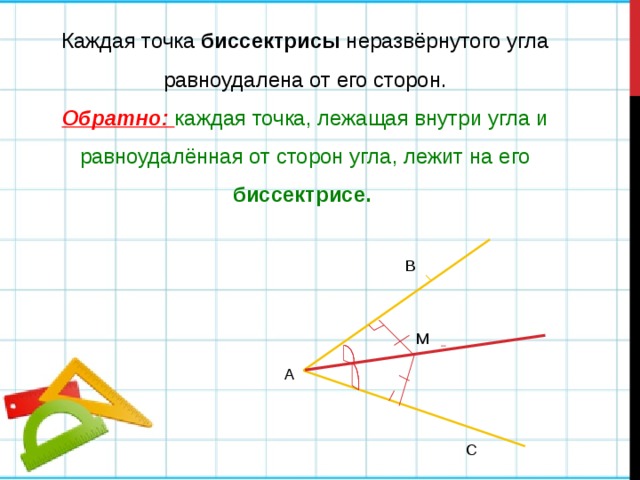
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
В
М
А
С
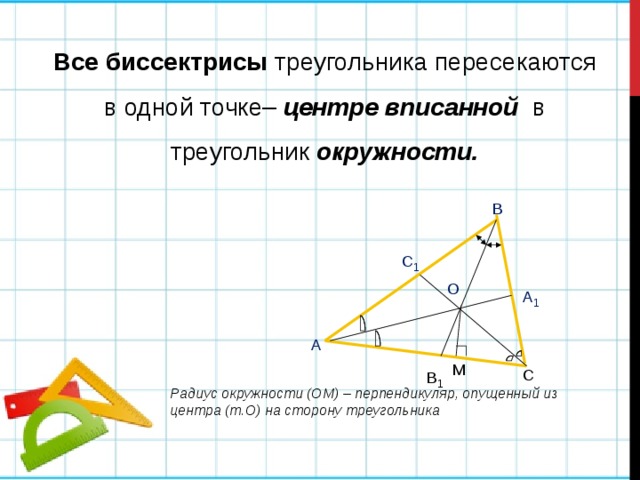
Все биссектрисы треугольника пересекаются в одной точке– центре вписанной в треугольник окружности.
В
С 1
О
А 1
А
М
В 1
С
Радиус окружности (ОМ) – перпендикуляр, опущенный из центра (т.О) на сторону треугольника
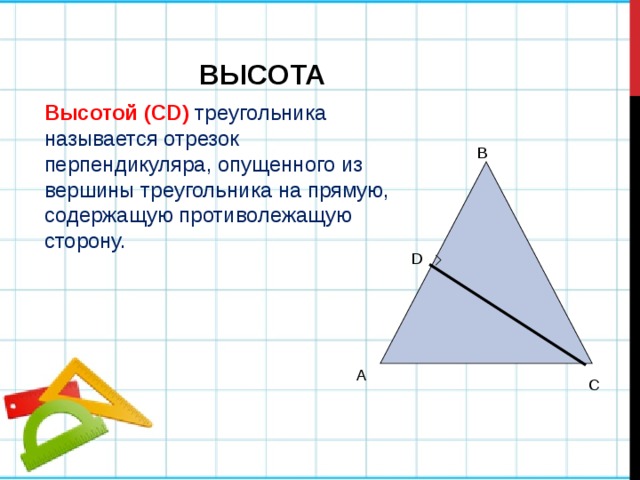
ВЫСОТА
Высотой (СD) треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на прямую, содержащую противолежащую сторону.
B
D
A
C
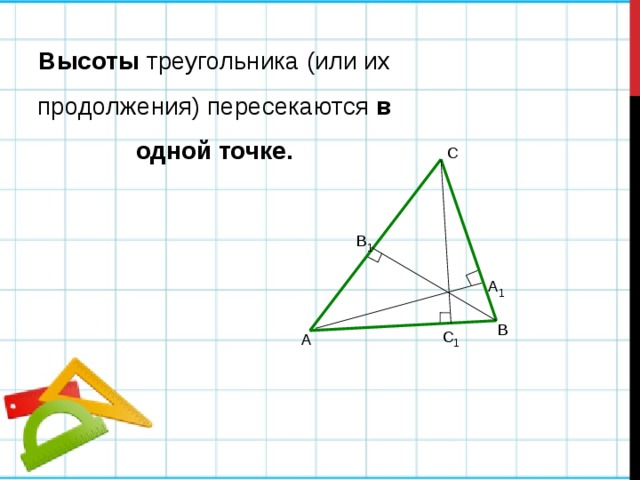
Высоты треугольника (или их продолжения) пересекаются в одной точке.
С
В 1
А 1
В
С 1
А
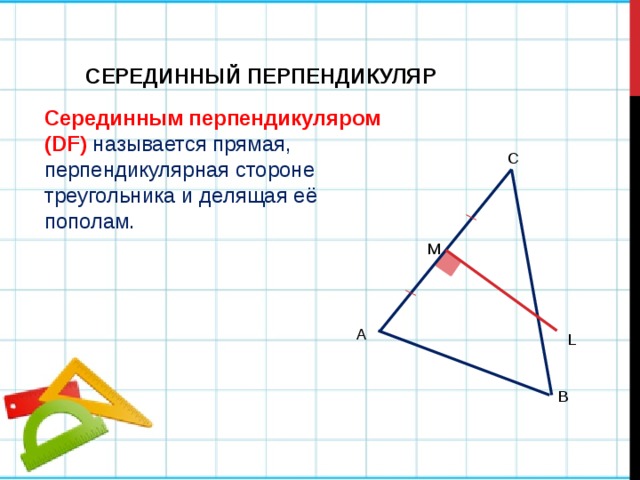
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Серединным перпендикуляром (DF) называется прямая, перпендикулярная стороне треугольника и делящая её пополам.
C
M
А
L
B
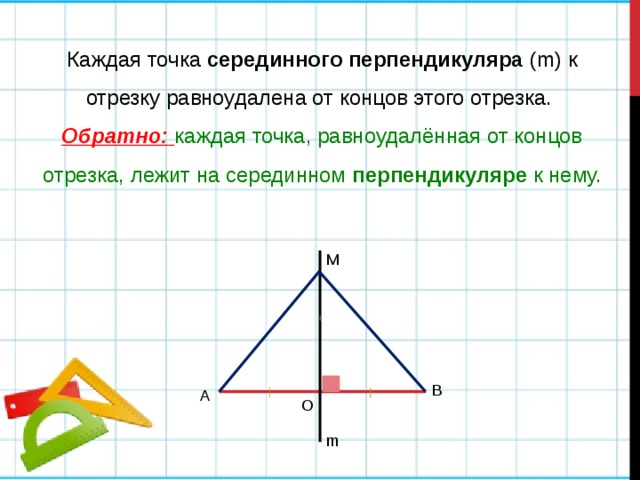
Каждая точка серединного перпендикуляра (m) к отрезку равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
М
В
А
O
m
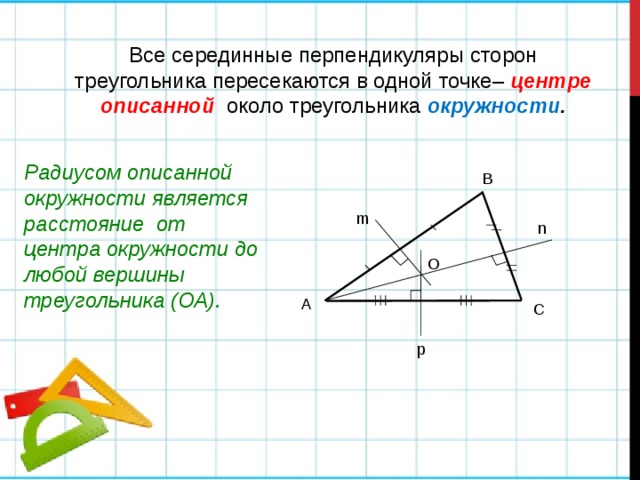
Все серединные перпендикуляры сторон треугольника пересекаются в одной точке– центре описанной около треугольника окружности .
Радиусом описанной окружности является расстояние от центра окружности до любой вершины треугольника (ОА).
В
m
n
О
А
С
p
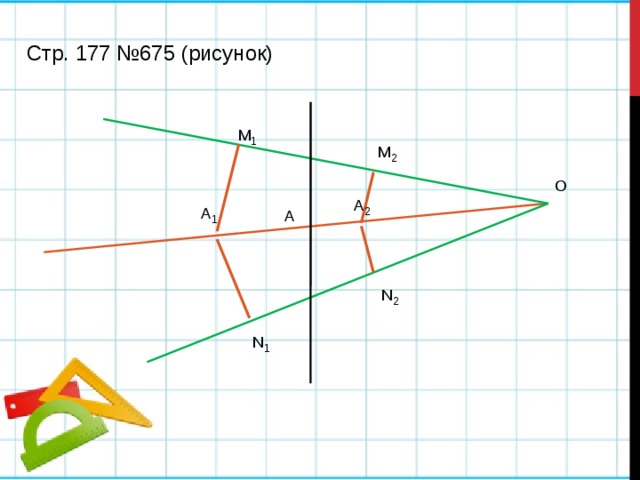
Стр. 177 №675 (рисунок)
М 1
М 2
O
А 2
А 1
А
N 2
N 1

Домашнее задание
Стр.173 § 3 определения и теоремы стр.177 № 675 (закончить)





