Урок по теме"Длина окружности"

План – конспект урока

Тема:

«Длина окружности» в 6-м классе.

Цели урока:

1.Обучающая.

Выведение формулы длины окружности , знакомство с числом π, обучение применению формулы при решении задач.

2.Развивающая:

развитие кругозора , мышления, внимания, культуры математической речи, привитие интереса к изучению математики.

3. Воспитательная:

воспитание ответственности, аккуратности, самостоятельности.

ПОБОЧНЫЕ ЦЕЛИ. Развивать интерес к математике путём создания ситуации успеха.

Оборудование:

предметы круглой формы: (стаканы различной величины, крышки, баночки), нитки, линейки, калькуляторы.

Ход урока.

1 этап. Оргмомент

Учитель. Отгадайте загадку, и вы узнаете, о чём сегодня на уроке пойдёт речь.

Если видишь солнце в небе, или чашку с молоком ,

Видишь бублик или обруч, слышишь сказку с колобком,

В круглом зеркале увидел ты сейчас свою наружность.

И вдруг понял, что фигура называется окружность.

2 этап. Актуализация опорных знаний.

Давайте вспомним, что мы уже знаем про окружность.

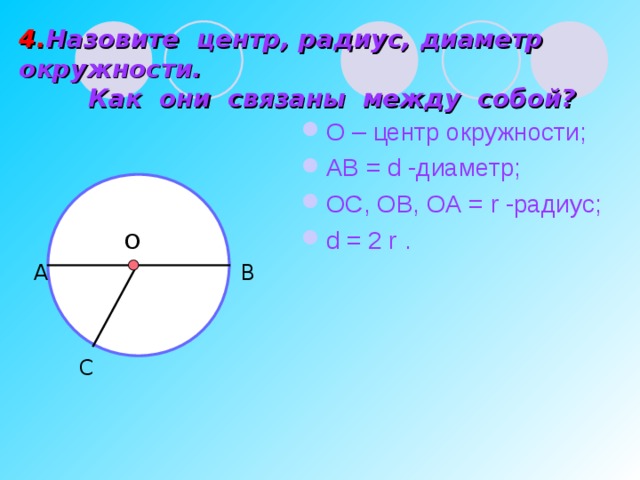
1.Назовите по рисунку радиус, диаметр. (r=d/2).

• Можно ли измерить длину , радиуса?

• С помощью какого измерительного прибора это можно сделать? Какими единицами измерения будет выражен результат?

• Можно ли измерить длину окружности? С помощью какого измерительного прибора это можно сделать? Как это можно сделать? (Возможные ответы: с помощью нитки, веревки и т.п.)

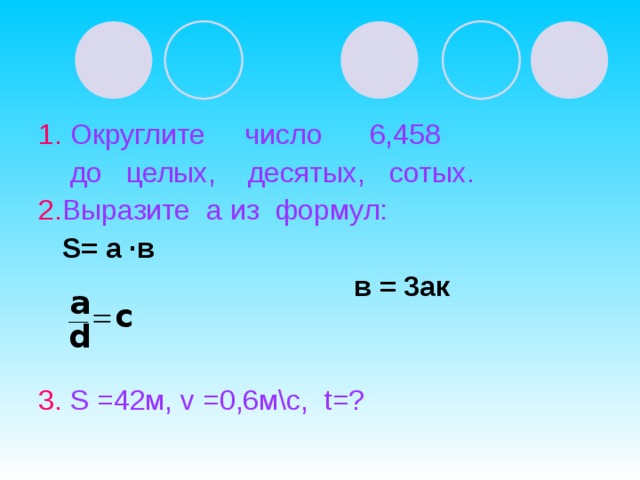
2.Округлите число 6,458 до десятых, сотых.

3.Выразите а из формул: s=а ·в, в=3а· к, а/d=c

4. s=42км, v=0,6, t=?

3 этап. Ознакомление с новым материалом. Практическая работа.

УЧИТЕЛЬ. Ниткой, веревкой удобно пользоваться для измерения длины окружности малого радиуса. А как быть, если требуется измерить длину окружности предмета круглой формы большого размера, например, трубы завода? С помощью нитки и веревки это сделать можно, но весьма трудоемко и результат таких измерений может быть неточным.

Давайте попробуем вывести формулу, по которой можно было бы вычислить длину окружности, зная ее радиус.

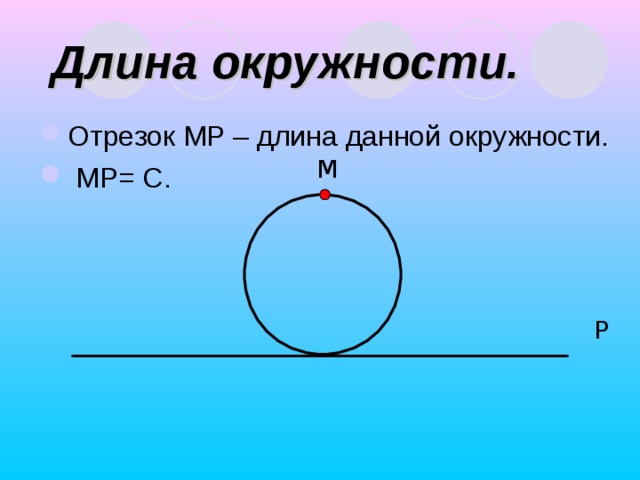
Возьмите каждый нитку, обвяжите ею цилиндр или другую модель окружности (т.е. измерьте длину окружности.), затем распрямите её, то длина нитки будет приблизительно равна длине окружности банки. Обозначьте её буквой С.

Чтобы получить более точный результат, нужно "опоясать" банку ниткой несколько раз, а затем длину всей нити разделить на количество "опоясывающих" кругов.

Запишите каждый в тетрадь С=… и укажите число, которое вы получили после измерения.

Теперь измерьте диаметр. Запишите d=…

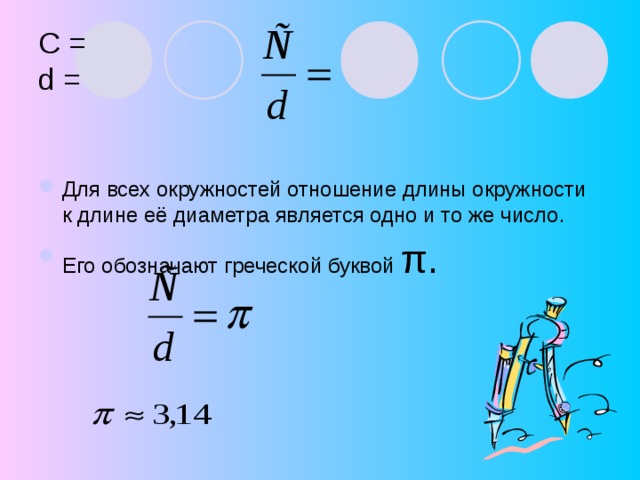
Найдите с помощью МК отношение длины окружности к её диаметру: С на d, и запишите полученное значение в тетерадь С/d=…

Учитель выписывает несколько результатов на доске. Все они примерно одинаковы: С/d3,14. ( или 3,1 3,2 )

ВЫВОД. Какими бы различными ни были окружности, отношения их длин к диаметрам будут постоянно одинаковыми

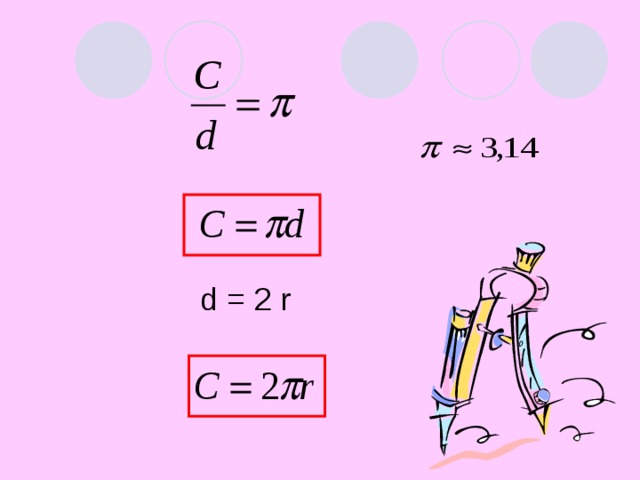
Если бы мы, ребята, еще более точно измерили длину окружности, ее диаметр и более точно выполнили вычисления длины окружности к ее диаметру, то получили бы число 3,14… Это число математики обозначают буквой (пи)

Это отношение известно со времён Архимеда, с его помощью можно найти длину окружности без нитки, измерив только диаметр или радиус. Зная, что =, выразим длину окружности С=

А так как d=2,то C=2r.

4. Историческая справка

В Древнем Египте(около 3500 лет назад) считали "Пи=3,16", древние римляне полагали, что "Пи=3,12".. С помощью современных машин число Пи было выражено с точностью до миллиона знаков после запятой. Для обозначения частного от деления длины окружности на диаметр впервые букву Пи использовал английский математик Джонс в 1706г, но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил Пи до 153 знаков после запятой. Итак: Пи- это бесконечная десятичная дробь.

Нам с вами нужно помнить не более 3-5 цифр этого числа. Если вы их забудете их, то задайте себе вопрос: что я знаю о кругах?

5этап. Первичное закрепление полученных знаний, умений и навыков. ( Образец)

ЗАДАЧА 1. R=3, п=3 С= 18

ЗАДАЧА 2.

ЗАДАЧА 3.

6 этап. Закрепление теории

7 этап. Психофизическая пауза.

8 этап. Закрепление навыка нахождения

4. Заключительное слово учителю.

Мы совершили путешествие в цирк. Чтобы подготовить замечательные выступления артистам тоже приходится решать задачи по математике. Вычисления выполняют и фокусники и акробаты. В цирке нужны не только знания по математике, но и другие науки.

Домашнее задание.

9 этап.Задание на дом: п249 до фразы « на рис.40…»,, N 867(851), N 868(852), 871(855), 864(848(1))

Приложение.

ИСТОРИЧЕСКАЯ СПРАВКА.(Готовят учащиеся)

1 ученик. (Демонстрирует плакат)

Небольшие стихотворения или яркие фразы дольше остаются в памяти, чем числа, поэтому для запоминания какого-либо числового значения p придумывают особые стихотворения или отдельные фразы. В произведениях этого вида математической поэзии слова подбирают так, чтобы число букв в каждом слове последовательно совпадало с соответствующей цифрой числа p

ЭТО Я ЗНАЮ И ПОМНЮ ПРЕКРАСНО,

3 1 4 1 5 9

ПИ МНОГИЕ ЗНАКИ МНЕ ЛИШНИ, НАПРАСНЫ.

2 6 5 3 5 8

В этой фразе количество букв в каждом слове равно цифре числа пи.

А вот ещё одна такая фраза.

КТО И ХОТЯ И СКОРО ВОЗЖЕЛАЕТ

ПИ УЗНАТЬ ЧИСЛО, УЖЕ ЗНАЕТ.

Первые четыре цифры этого числа можно запомнить по числу букв в каждом слове следующей фразы:

Что я знаю о круге

= 3 1 4 1 5

2 УЧЕНИК ЭТО УДИВИТЕЛЬНОЕ ЧИСЛО p.

Любой школьник вычисляет теперь длину окружности по диаметру гораздо точнее, чем мудрейший жрец страны пирамид или самый искусный архитектор великого Рима. На ранних ступенях человеческого развития пользовались неточным числом p. Оно было равно 3. Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта.

В 3в. до н.э. Архимед без измерений одними рассуждениями вычислил точное значение числа p=22/7 .

Математик шестнадцатого века Лудольф, в Лейдене, имел терпение вычислить его с 35 десятичными знаками и завещал вырезать это значение для p на своём могильном памятнике.

Малоизвестный математик Шенкс в 1873 г. опубликовал такое значение числа p, в котором после запятой следовало 707 десятичных знаков, но, начиная с 528-го знака, он ошибся. Такие длинные числа, приближённо выражающие значение числа p, не имеют ни практической, ни теоретической ценности. Только для безделья да в погоне за дутыми «рекордами» могло в наше время желание «переплюнуть» Шенкса.

В 1940-х в Англии и США нашлись математики, которые в погоне за рекордом вычислили 808 знаков числа p и были польщены тем, что в вычислениях Шенкса обнаружили ошибку. Два обычных вычислений с числом p вполне достаточно запомнить два знака после запятой (3, 14).

=3,1415965358979323846264

4. Выступление ученика с историческим сообщением о числе .

Число - бесконечная десятичная дробь. - первая буква греческого слова окружность, периферия. Это отношение известно со времен Архимеда, его считали равным . Для закрепления в памяти рационального выражения числа Архимеда - , может оказаться полезной шутка из учебника Магницкого.

Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах.
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов

Впервые обозначение ввел в 1706 году английский математик Джонс, общепринятым это обозначение стало в 1736 году после одной из работ Эйлера, великого математика, физика, астронома.

=3,141592653589793238462643…(24 знака)

Вычисление как можно большего числа точных цифр числа с помощью компьютера занимает математиков и в настоящее время. Так, в 1988 году, японский ученый Ясума Канеда вычислил 400 млн точных цифр после запятой. Это не только спортивный интерес, необходимо и для изучения случайных процессов. В школьном же курсе математики =3,14.

Учитель: Продолжаем работать . Подбери противоположное по значению слово

Продолжить по аналогии:

плюс-минус;

умножение-

уменьшение-

известное-

простое-

тупой-

прямая-

числитель-

целое-

правильная-неправильная?

ИСТОРИЧЕСКАЯ СПРАВКА.

1 ученик. (Демонстрирует плакат)

Небольшие стихотворения или яркие фразы дольше остаются в памяти, чем числа, поэтому для запоминания какого-либо числового значения Π придумывают особые стихотворения или отдельные фразы. В произведениях этого вида математической поэзии слова подбирают так, чтобы число букв в каждом слове последовательно совпадало с соответствующей цифрой числа Π

ЭТО Я ЗНАЮ И ПОМНЮ ПРЕКРАСНО,

3 1 4 1 5 9

ПИ МНОГИЕ ЗНАКИ МНЕ ЛИШНИ, НАПРАСНЫ.

2 6 5 3 5 8

В этой фразе количество букв в каждом слове равно цифре числа пи.

А вот ещё одна такая фраза.

КТО И ХОТЯ И СКОРО ВОЗЖЕЛАЕТ

ПИ УЗНАТЬ ЧИСЛО, УЖЕ ЗНАЕТ.

Первые четыре цифры этого числа можно запомнить по числу букв в каждом слове следующей фразы:

Что я знаю о круге

Π= 3 1 4 1 5

2 УЧЕНИК ЭТО УДИВИТЕЛЬНОЕ ЧИСЛО p.

Любой школьник вычисляет теперь длину окружности по диаметру гораздо точнее, чем мудрейший жрец страны пирамид или самый искусный архитектор великого Рима. На ранних ступенях человеческого развития пользовались неточным числом p. Оно было равно 3. Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта.

В 3в. до н.э. Архимед без измерений одними рассуждениями вычислил точное значение числа Π = . Для закрепления в памяти рационального выражения числа Архимеда - , может оказаться полезной шутка из учебника Магницкого.

Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах.
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов

Впервые обозначение ввел в 1706 году английский математик Джонс, общепринятым это обозначение стало в 1736 году после одной из работ Эйлера, великого математика, физика, астронома.

=3,141592653589793238462643…(24 знака)

Математик шестнадцатого века Лудольф, в Лейдене, имел терпение вычислить его с 35 десятичными знаками и завещал вырезать это значение для p на своём могильном памятнике.

Малоизвестный математик Шенкс в 1873 г. опубликовал такое значение числа p, в котором после запятой следовало 707 десятичных знаков, но, начиная с 528-го знака, он ошибся. Такие длинные числа, приближённо выражающие значение числа p, не имеют ни практической, ни теоретической ценности. Только для безделья да в погоне за дутыми «рекордами» могло в наше время желание «переплюнуть» Шенкса.

В 1940-х в Англии и США нашлись математики, которые в погоне за рекордом вычислили 808 знаков числа p и были польщены тем, что в вычислениях Шенкса обнаружили ошибку. Вычисление как можно большего числа точных цифр числа с помощью компьютера занимает математиков и в настоящее время. Так, в 1988 году, японский ученый Ясума Канеда вычислил 400 млн точных цифр после запятой. Это не только спортивный интерес, необходимо и для изучения случайных процессов.

Два обычных вычислений с числом p вполне достаточно запомнить два знака после запятой (3, 14).

с=2πr

c=πd

ДЖОНС

1706 г.

π≈3,14…

ЛЕОНАРД

ЭЙЛЕР

1736 г.

АРХИМЕД

III век до н.э.

Математика - 6 класс.

Длина окружности .

Автор - учитель математики Прытков Игорь Юрьевич.

МБОУ Авангардовская ООШ.

Отгадайте загадку, и вы узнаете, о чём сегодня на уроке пойдёт речь.

Если видишь солнце в небе, или чашку с молоком,

Видишь бублик или обруч, слышишь сказку с колобком,

В круглом зеркале увидел ты сейчас свою наружность

И вдруг понял, что фигура называется ….

Классная работа.

Длина окружности.

• Выведение формулы длины окружности ;
• Знакомство с числом π;
• Обучение применению формулы при решении задач.

Девиз:

Математику нельзя изучать,наблюдая,

как это делает сосед!

1. Округлите число 6,458

до целых, десятых, сотых.

2. Выразите а из формул:

S= а ·в

в = 3ак

3. S =42м, v =0,6м\с, t=?

4. Назовите центр, радиус, диаметр окружности. Как они связаны между собой?

• О – центр окружности;
• АВ = d -диаметр;
• ОС, ОВ, ОА = r -радиус;
• d = 2 r .

О

А

В

С

Длина окружности.

• Отрезок МР – длина данной окружности.
• МР= С.

М

Р

• Для всех окружностей отношение длины окружности к длине её диаметра является одно и то же число.
• Его обозначают греческой буквой π.

C = d =

d = 2 r

Из истории термина

Из древнеегипетских и вавилонских источников известно,что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали  равное 3,12.

В Древнем Египте  считали равным 3,16…

В истории математики известно, что первое вычисление числа π , обозначающего отношение длины окружности к её диаметру, было выполнено выдающимся математиком древности Архимедом (287-212 г.г. до н.э.).

Он установил, что  = 3,14…

Впервые обозначение числа π ввёл в 1706 году английский математик Джонс.

Русский математик Леонард Эйлер вычислил  с точностью до 153 десятичных знаков. Именно он в 1736 г ввел число  (первая буква в греческом слове «перифериа» - окружность ) для отношения длины окружности к длине её диаметра.

• Как вычислить длину окружности , зная её радиус?
• Как вычислить длину окружности , зная её диаметр?
• Каково соотношение диаметра и радиуса одной окружности?
• Чему равно число

d = 2 r

№ 838

С = 40,8 м

D - ?

Окружность арены во всех цирках мира имеет длину 40,8 м. Найдите диаметр арены ( П округлите до целых)?

2дм

7 5 р а з !

Устно. На представлении в цирке кошка показала необычайно развитый вестибулярный аппарат. Она пробежала 75 раз по круглой тумбочке, радиус которой 2 дм! Какое расстояние она пробежала?

Число П округлите до целых.

диаметр

4дм

с=2 πr

c= πd

Устно. Какое расстояние проедет петух на колесе, диаметр которого 4 дм, за 1 оборот? За 3 оборота? За 10 оборотов? За n оборотов? Число П округлите до десятых.

12,4дм

?

радиус

?

4,5дм

Устно. За 1 оборот колесо, на котором едет медвежонок, проехало 27,9 дм. Найти радиус колеса. Число П округлите до десятых.

27,9 дм

t = 3c

?

v = 4м/с

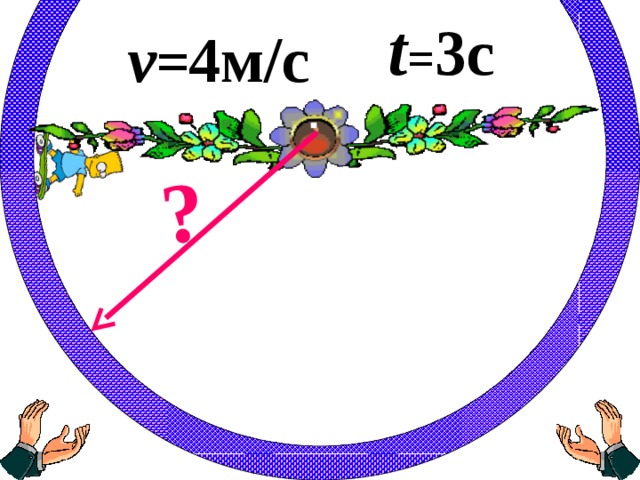
Устно. В программе принимает участие Барт Симпсон. Он на своём скейтборде проехал расстояние, равное половине всей окружности колеса, за 3 секунды. Найдите радиус окружности этого колеса, если скорость мальчика 4 м/с. (П=3)

105 оборотов

?

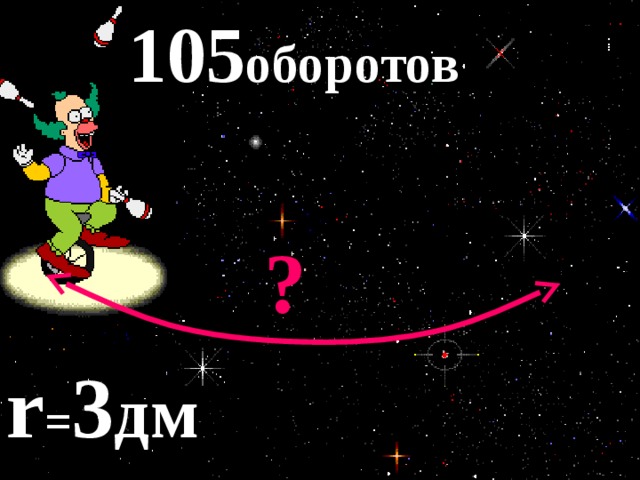
Клоун Красти удивил зрителей не меньше. Он проехал по арене на велосипеде, одновременно жонглируя кеглями. Какое расстояние он проехал, если колесо его велосипеда, радиусом 3 дм, обернулось 105 раз. Ответ выразить в метрах и округлить до единиц. (П=3,14)

r = 3 дм

20м

2мин

300 м/мин

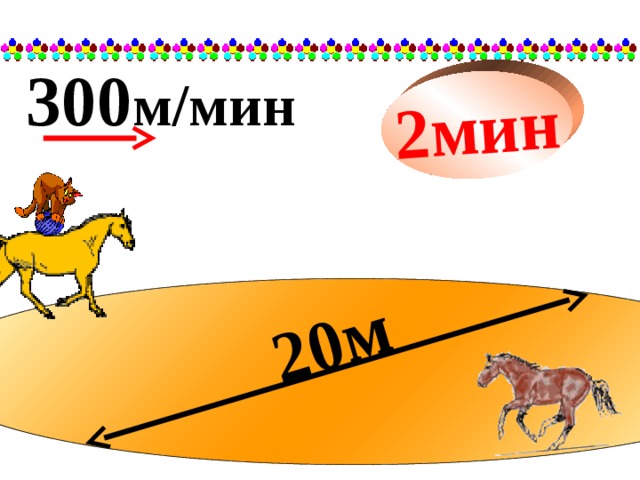
По арене цирка, диаметр которой 20 м, скачут лошади, со скоростью 300 м/мин. Сколько кругов проскачут лошади за 2 мин? Сколько прыжков выполнит кот – акробат за это же время, если за один круг он делает 26 прыжков?

Число П округлите до целых.

150

2м

О

Б

О

Р

О

Т

О

В

В

Р

Е

М

Я

?

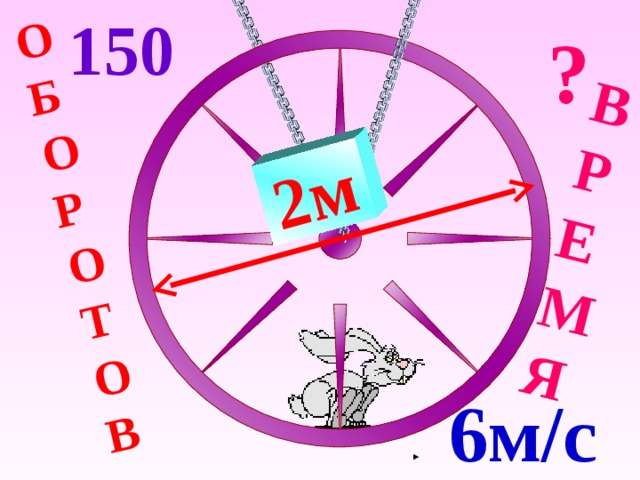
Мне запомнился аттракцион «Заяц в колесе». Сколько времени длился этот номер цирковой программы, если диаметр колеса 2 м, скорость зайца 6 м/с и колесо сделало 150 оборотов. (П=3,14)

6м/с

2,4м

обернулось 1250 раз

оборотов?

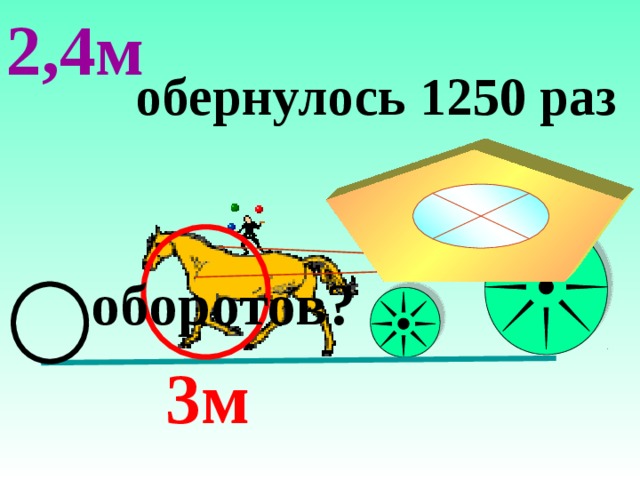
Г.В.Дорофеев, Л.Г.Петерсон. 6 класс №198(4). Маленькое колесо повозки, имеющее окружность 2,4 м, обернулось на некотором расстоянии 1250 раз. Сколько раз обернулось на этом расстоянии большое колесо, имеющее окружность 3 м?

Доп. вопросы: а) на сколько процентов больше оборотов сделало первое колесо? б) на сколько процентов меньше оборотов сделало второе колесо? в) Почему передняя ось повозки больше стирается и чаще загорается, чем задняя?

3м

3м

5м

6м/с

14 м/с

4 мин

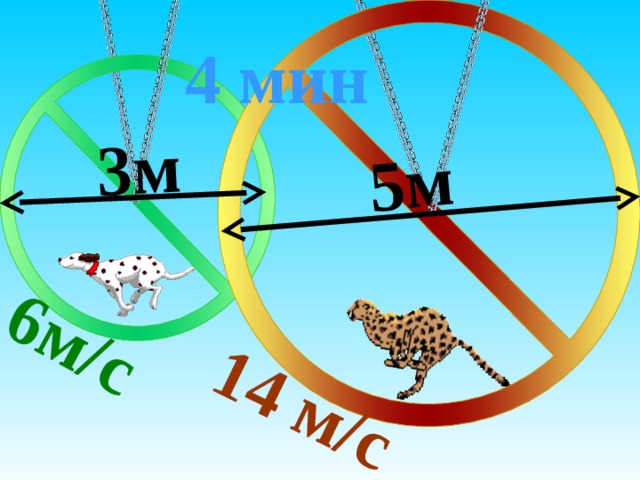
«Звери в колесе». Собака в колесе, диаметром 3м, мчится со скоростью 6 м/с. Гепард в колесе, диаметр которого 5м, развил скорость 14 м/с. Какое колесо сделает больше оборотов за 4 минуты? (П=3)

d=1дм

350 оборотов

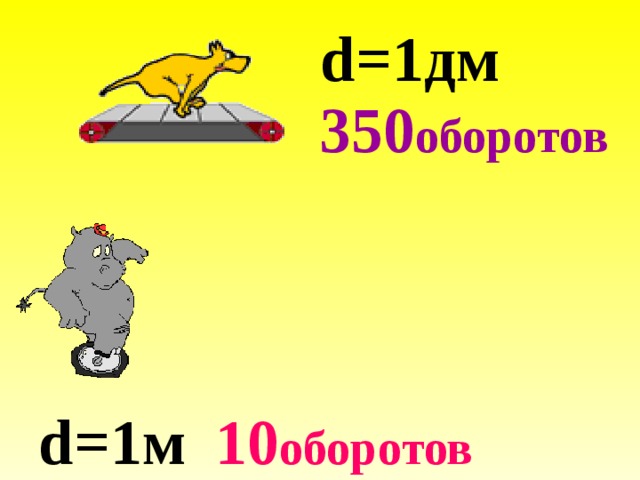
Удивительный конкурс: кто преодолел большее расстояние? Диаметр колеса велосипеда у бегемотика 1м и и оно сделало 10 оборотов. Диаметр колёс беговой дорожки, по которой бежит пёс, всего 1 дм, но это колёсико сделало 350 оборотов.

d=1м

10 оборотов

Домашнее задание:

• п.24 ( до фразы « на рис.40 »)
• № 852
• № 855
• № 848 (1)

Подведём итог урока.

• За что ты можешь себя похвалить?

• Что тебе удалось на уроке?

• Над чем ещё нужно поработать?

• Зачем нам нужен был этот урок?

Спасибо за урок.