Методы решения систем уравнений
Цели:
Обобщить знания и закрепить умения учащихся решать системы уравнений второй степени различными способами. Подготовиться к контрольной работе.
Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы, формировать умения чётко и ясно излагать свои мысли.
Воспитывать умение работать с имеющейся информацией, умение слушать товарищей, содействовать воспитанию интереса к математике, активности, мобильности, общей культуре.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: компьютер, проектор, тестовые знания.
Ход урока
Организационный момент (слайд 1) Пусть каждый день и каждый час
Вам новое добудет
Пусть добрым будет ум у вас
А сердце умным будет.
На доске ученики решают домашнее задание
ДКР №1(№4,5,6)
1 вариант
№ 4 x² - 3y² = 4,
x + y = 6. Ответ: (14; -8), (4; 2).
№ 5 x² - 2y² = -4,
x² + 2y² = 12. Ответ: (2; 2), (2; -2),(-2; 2),(-2; -2).
№ 6 (xy)² + 3y = 45,
5y - 2xy = 3. Ответ: (2; 3), (3 9/57; - 2 7/25).
2 вариант
№ 4 2x² - y² = 14,
3x + 2y = 5. Ответ: (3; -2), (27; -38).
№ 5 3x² + y² = 7,
x² + 2y² = 9. Ответ: (1; 2), (-1; 2),(1; -2),(-1; -2).
№ 6 (xy)² - 3xy = 18,
4x + y = 1. Ответ: (1; -3), (-3/4; 4).
Остальные фронтальный опрос
Фронтальный опрос (слайды 2-7)
1.Что называется системой уравнений второй степени?
Несколько уравнений, для которых надо найти значения переменных удовлетворяющих одновременно всем уравнениям
p
(x;y)=0,
q(x;y)=0.
2. Что называется решением системы уравнений второй степени?
Пара чисел (x;y) которая одновременно является решением каждого уравнения
3. Что значит решить систему уравнений второй степени?
Найти все её решения или установить, что решений нет
4. Какое свойство используется при решении систем уравнений?
Свойство равносильности
5. Какие методы решений систем уравнений вы знаете?
Графический метод (алгоритм)
Построить в одной системе координат график каждого уравнения.
Определить координаты точки пересечения.
Записать ответ: (х; у).
Установите соответствие между системой уравнений и рисунком , на котором представлен его график:
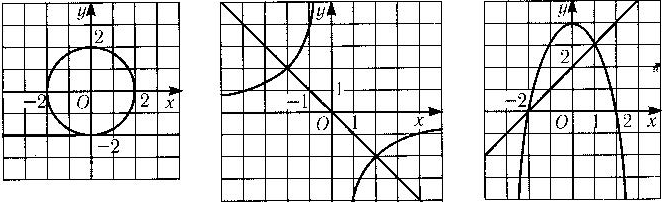
1 2 3
a)
x²+y=4, б) y+2=0, в) x+y=0,
x-y+2=0; x²+y²=4; xy=4.
Ответ: 1-б; 2-в; 3-а.
Метод подстановки (алгоритм)
Из какого-либо уравнения выразить одну переменную через другую.
Подставить полученное выражение для переменной в другое уравнение.
Решить полученное уравнение.
Подставить каждый из найденных значений переменной и вычислить значение второй переменной.
Записать ответ: (х; у).
Ка
кой ученик применил метод наиболее рационально: x²+y²+3xy=-1,
x+2y=0.
x ²=-y²-3xy-1, б) x²+y²+3xy=-1, в) x²+y²+3xy=-1,
x+2y = 0. 2y = -x. x = -2y.
Метод сложения (алгоритм)
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: (х; у).
Проверьте решение системы уравнений:
x ²-2y²=14,
x²+2y²=18.
2x²=32,
x²=16
x=4. Ответ: 4
Метод введения новой переменной (алгоритм)
Метод введения новых переменных применяется при решении систем двух уравнений с двумя переменными одним из следующих способов:
Вводится одна новая переменная только для одного уравнения системы;
Вводятся две новые переменные сразу для обоих уравнений.
6. Каким методом вы решали бы следующие системы уравнений:
; 
; 
; 
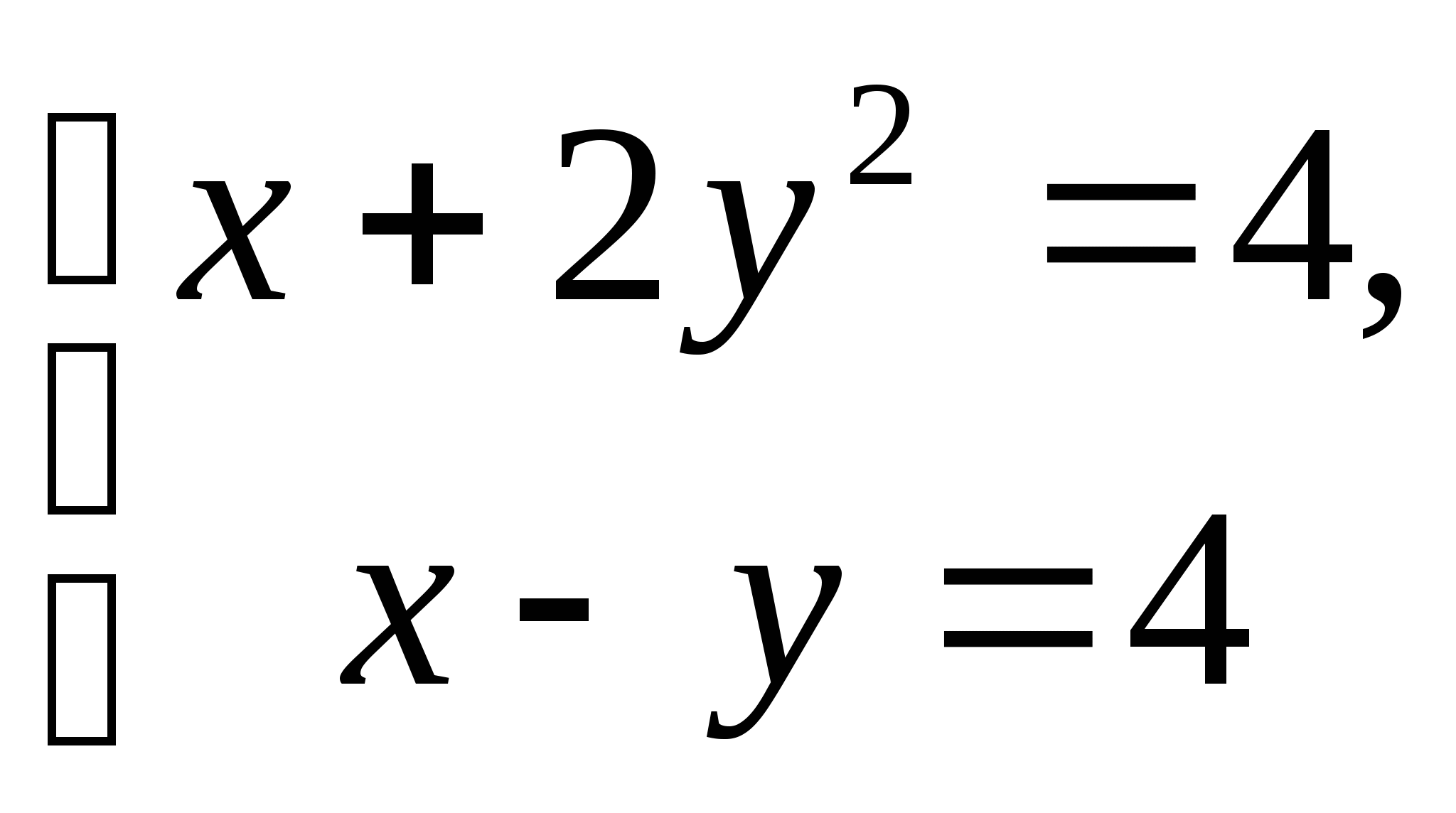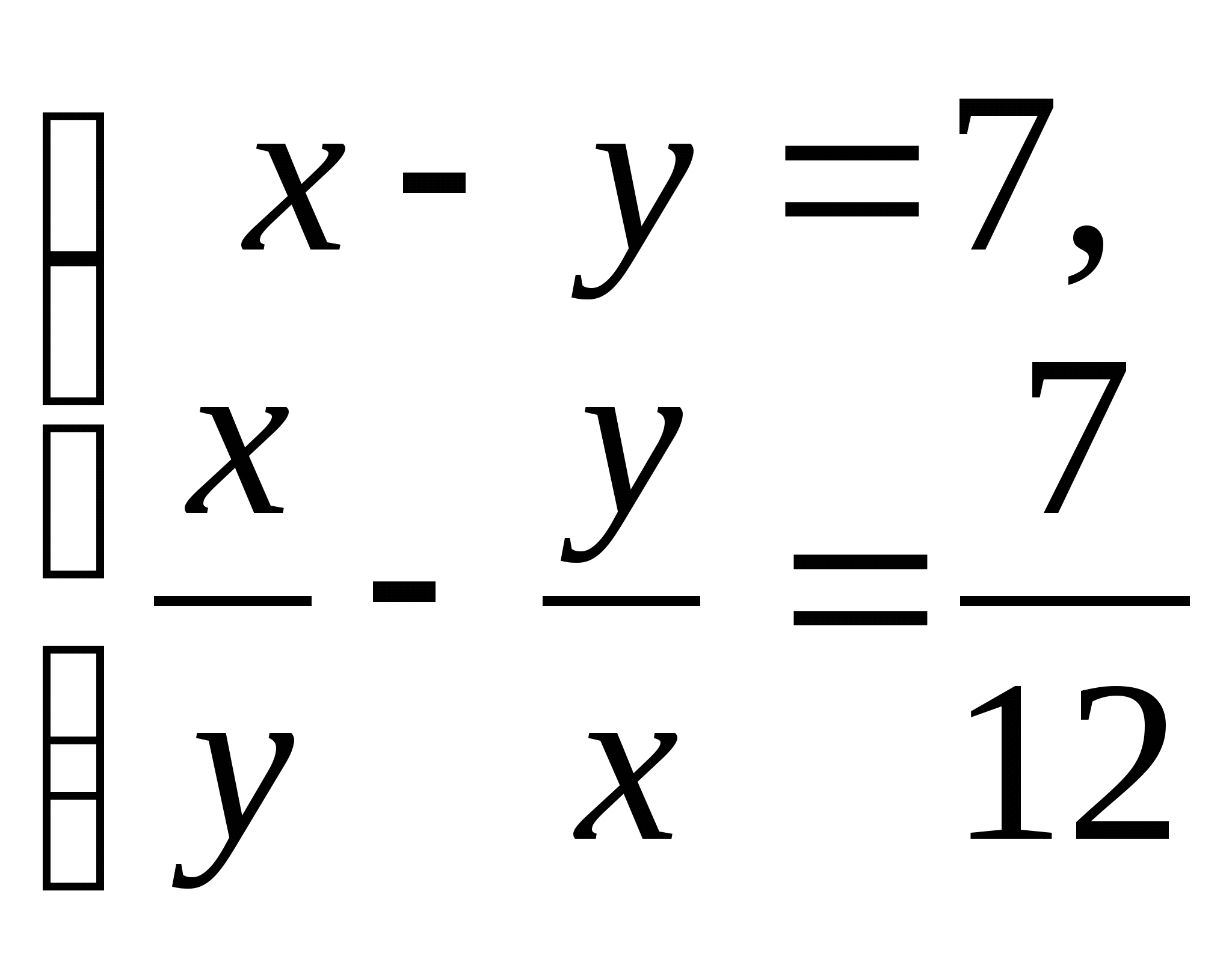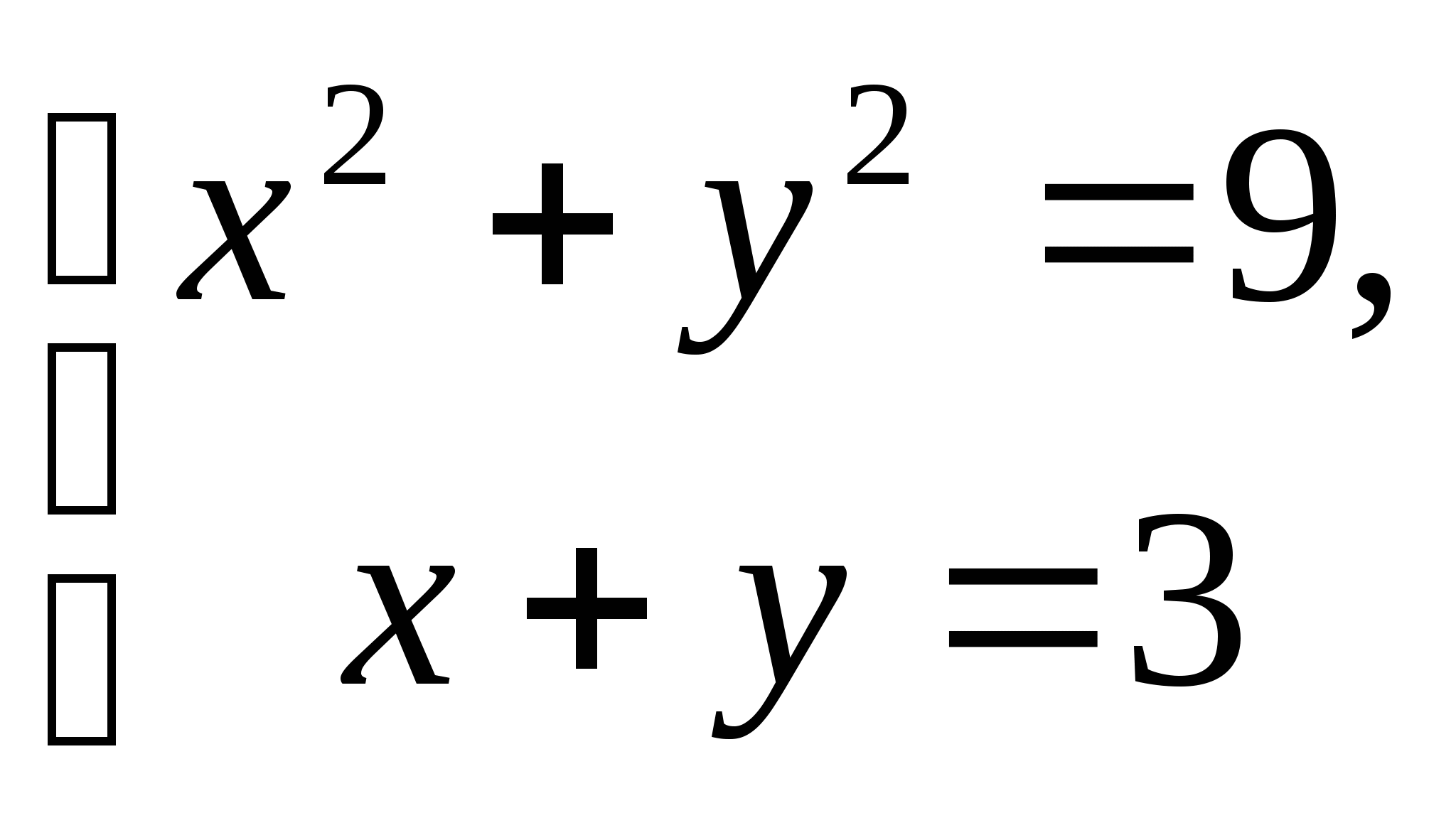
( x+2)²+(y-3)²=9,
y=
.
Проверка домашнего задания
ДКР № 1 (№4,5,6)
Запишем тему урока:
Методы решения систем уравнений
Решение упражнений:
x²
+ xy = 12, {x - 6y = -2, {x + y = 5,
y – x =2. 2x + 3y = 11. xy = - 14.
Ответ: (2; 4),(-3; -1). Ответ:( 4; 1). Ответ: (-2; 7), (7; -2).
Физкультминутка
Самостоятельная работа (выполнение теста)
I вариант
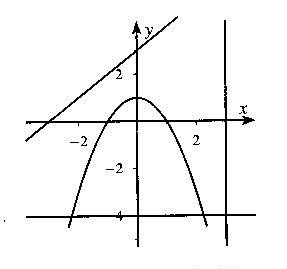
На рисунке изображены графики функций. Укажите систему уравнений, которая не имеет решений.
a
) y = 2 -x², б) y = 2- x², в) y = 2- x², г) таких систем нет.
y+4 = 0; x- y = -3; x-3 = 0;
2. Укажите систему уравнений, которая является математической моделью ситуации, описанной в задаче: «Площадь прямоугольного треугольника с катетами x и y равна 60см², а его гипотенуза равна 17»
а) x + y = 17, б) x² + y² = 17, в) x² + y² = 289, г) x² + y² = 289,
x y = 60; x+ y = 30; x y = 60; x y = 120;
Ре шите систему уравнений: x² + y² +2xy = 9,
x –y = 1;
а) (2;1); (-1;-2) б) (-2;1); (-1;-2) в) (-2; -1); (1;2); г) (-1;2); (2; -1).
Ответ: 1б; 2г; 3а.
II вариант
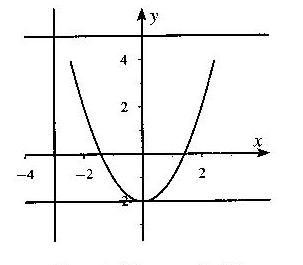
На рисунке изображены графики функций. Укажите систему уравнений, которая не имеет решений.
a ) y = x²-2, б) y = x²-2, в) y = x²-2, г) все три системы.
x+3 = 0; y+3 = 0; y-5 = 0;
Укажите систему уравнений, которая является математической моделью ситуации описанной в задаче: «Площадь прямоугольного треугольника с катетами x и y равна 84см², а его гипотенуза равна 25»
а) 
x + y = 25, б) x² + y² = 25, в) x² + y² = 625, г) x² + y² = 625,
x y = 84; x+ y = 42; x+ y = 168; x y = 84;
Ре шите систему уравнений: x² + y² -2xy = 1,
x + y = 3;
а) (-2;5); (5;-2) б) (2;1); (1;2) в) (-2; 1); (1;2); г) (-1;-2); (2; 1).
Ответ: 1б; 2в; 3б.
I и II вариант решают тест, сдают учителю на проверку, у себя оставляют ответы,
Можно проверить правильность выполнения.
Рефлексия(15 слайд)
Я все знаю, понял и могу объяснить другим!
Я все знаю, понял, но не уверен, что смогу объяснить другому.
Я сам знаю, понял, но объяснить другому не смогу.
У меня остались некоторые вопросы.
СПАСИБО!
Благодарю всех за проделанную работу
Порой задача не решается,
Но это, в общем, не беда.
Ведь солнце все же улыбается,
Не унывайте никогда.
Друзья тебе всегда помогут
Они с тобой, ты не один.
Поверь в себя – и ты все сможешь.
Иди вперед и победишь.
Задание на дом: Домашняя контрольная работа №2
