Тренировочные задания по подготовке к ОГЭ по математике

Квадрат

1. Сторона квад­ра­та равна 10. Най­ди­те его площадь.

2. Периметр квад­ра­та равен 40. Най­ди­те площадь квадрата.

3. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

4.  Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

5.  Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

6.  Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 83.

Прямоугольник

1. Задание 18 № 169864

В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сторона равна 12. Най­ди­те площадь прямоугольника.

2. Задание 18 № 169867

В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на  .

3. Задание 18 № 169898

В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны  . Най­ди­те площадь прямоугольника, деленную на 

4. Задание 18 № 311761

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

5. Задание 18 № 311849

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

6. Задание 18 № 316321

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше другой.

7. Задание 18 № 324077

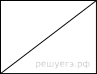В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

Параллелограмм

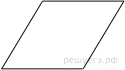
1. 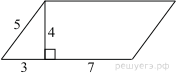 Найдите пло­щадь параллелограмма, изображённого на рисунке.

2. Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

3. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

4. Периметр ромба равен 24, а синус од­но­го из углов равен  . Най­ди­те площадь ромба.

5. Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

6. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на  .

7. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен  . Най­ди­те площадь параллелограмма.

8. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен  . Най­ди­те площадь параллелограмма.

9. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен  . Най­ди­те площадь параллелограмма.

10. В ромбе сто­ро­на равна 10, одна из диагоналей —  , а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

11.

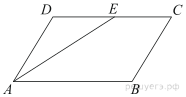
Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

12. 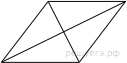 Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

13. 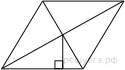 Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

14.

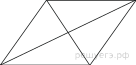
Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

15.  Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

16.

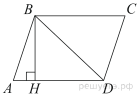
Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

17.

Высота BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 5 и HD = 8. Най­ди­те площадь ромба.

18.  Площадь ромба равна 54, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

19.

Высота   ромба   делит его сторону   на отрезки   и  . Найдите площадь ромба.

Квадрат

1. Сторона квад­ра­та равна 10. Най­ди­те его площадь.

Решение.

Площадь квадрата равна квадрату его стороны, поэтому она равна 100.

 

Ответ: 100.

2. Периметр квад­ра­та равен 40. Най­ди­те площадь квадрата.

Решение.

Периметр квадрата равен сумме длин всех его сторон. Таким образом, сторона квадрата равна 10. Площадь квадрата равна квадрату его стороны, поэтому она равна 100.

 

Ответ: 100.

3.

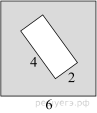
Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

Решение.

Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.

 

Ответ: 28.

4.  Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

Решение.

Все стороны квадрата равны, поэтому сторона длина стороны квадрата равна   Найдём площадь квадрата как квадрат его стороны: 

 

Ответ: 1600.

5.  Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

Решение.

Диагонали квадрата равны. Площадь квадрата можно найти как половину произведения его диагоналей: 

 

Ответ: 0,5.

6.  Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 83.

Решение.

Пусть   и   соответственно радиус и диаметр окружности,   — сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:

 

 

Ответ: 27 556.

Прямоугольник

1. Задание 18 № 169864

В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сторона равна 12. Най­ди­те площадь прямоугольника.

Решение.

Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.

 

Ответ: 120.

2. Задание 18 № 169867

В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на  .

Решение.

Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен половине гипотенузы. Поэтому одна из сторон прямоугольника равна 5. По теореме Пифагора найдем вторую строну:  Площадь прямоугольника равна произведению его смежных сторон, имеем:

 

 

Ответ: 25.

 

----------

В открытом банке иррациональный ответ.

3. Задание 18 № 169898

В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны  . Най­ди­те площадь прямоугольника, деленную на 

Решение.

Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтому СD = 5. Площадь прямоугольника равна произведению его смежных сторон:

 

 

Ответ: 25.

 

Примечание:

Вторую сторону можно было найти из определения синуса.

 

----------

В открытом банке иррациональный ответ.

4. Задание 18 № 311761

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

Решение.

Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника. Тогда периметр прямоугольника равен  откуда   Поэтому площадь прямоугольника равна 

 

Ответ: 120.

5. Задание 18 № 311849

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

Решение.

Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна   Следовательно, периметр прямоугольника равен

откуда   Поэтому площадь прямоугольника равна 

 

Ответ: 176.

6. Задание 18 № 316321

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше другой.

Решение.

Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника, тогда другая сторона равна   Следовательно, периметр прямоугольника равен

откуда   Поэтому площадь прямоугольника равна 

 

Ответ: 204.

7. Задание 18 № 324077

В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

Решение.

Пусть a и b — длины сторон прямоугольника, c — длина диагонали. Рассмотрим прямоугольный треугольник, образованный диагональю и сторонами треугольника, из теоремы Пифагора найдём вторую сторону прямогуольника:

 

 

Найдём площадь прямоугольника как произведение его сторон:

 

 

Ответ: 2688.

Параллелограмм

1.  Найдите пло­щадь параллелограмма, изображённого на рисунке.

Решение.

Площадь параллелограмма равна произведению длины основания на высоту:

 

 

 

Ответ: 40.

2. Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

Решение.

Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали:   Тогда вся неизвестная диагональ равна 8.

Площадь ромба равна половине произведения диагоналей:

 

Ответ: 24.

3. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Решение.

Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними. Таким образом,

 

Ответ: 50.

4. Периметр ромба равен 24, а синус од­но­го из углов равен  . Най­ди­те площадь ромба.

Решение.

Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними, поэтому

 

 

Ответ: 12.

5. Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

Решение.

Площадь параллелограмма равна произведению высоты на основание. Таким образом,

 

Ответ: 120.

6. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на  .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

 

 

Ответ: 30.

 

----------

В открытом банке иррациональный ответ.

7. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен  . Най­ди­те площадь параллелограмма.

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними, поэтому

 

Ответ: 20.

8. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен  . Най­ди­те площадь параллелограмма.

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:

 

 

Таким образом,

 

 

Ответ: 20.

9. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен  . Най­ди­те площадь параллелограмма.

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:

 

Таким образом,  , где x — число.

По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:

 

.

В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:

 

Таким образом,

 

Ответ: 20.

10. В ромбе сто­ро­на равна 10, одна из диагоналей —  , а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

Решение.

Площадь ромба равна произведению сторон на синус угла между ними:

 

 

Ответ:50.

 

Примечание:

 

Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.

11.

Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

Решение.

Диагональ параллелограмма делит его на два равных треугольника, поэтому   Медиана треугольника делит его на два равновеликих треугольника, поэтому  Следовательно,

 

 

 

Ответ: 42.

12.  Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

Решение.

Площадь ромба можно найти как половину произведения его диагоналей: 

 

Ответ: 42.

13.  Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

Решение.

Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что   и   получаем   Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники   и  , они прямоугольные,    следовательно, треугольники   и   равны, откуда   то есть высота   Найдём площадь ромба как произведение стороны на высоту:

 

 

Ответ: 18.

14.

Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

Решение.

Введём обозначения, как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть   Рассмотрим треугольник   он прямоугольный, из теоремы Пифагора найдём 

 

 

Найдём площадь ромба как половину произведения его диагоналей:

 

 

Ответ: 2400.

15.  Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Решение.

Проведём высоту в ромбе и введём обозначения, как показано на рисунке. Все стороны ромба равны, поэтому  Найдём   из прямоугольного треугольника 

 

 

Найдём площадь ромба как произведение стороны на высоту:

 

 

Ответ: 420,5.

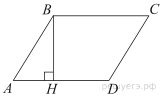
16.

Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

Решение.

Из прямоугольного треугольника   по теореме Пифагора найдём 

 

 

Площадь параллелограмма равна произведению основания на высоту:

 

 

Ответ: 1305.

17.

Высота BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 5 и HD = 8. Най­ди­те площадь ромба.

Решение.

Из прямоугольного треугольника   найдём 

 

 

Площадь ромба можно найти как произведение основания на высоту:

 

Ответ: 156.

18.  Площадь ромба равна 54, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

Решение.

Пусть сторона ромба равна a, тогда

 

Ответ: 6.

19.

Высота   ромба   делит его сторону   на отрезки   и  . Найдите площадь ромба.

Решение.

Из прямоугольного треугольника   найдём 

 

 

Площадь ромба можно найти как произведение основания на высоту:

 

Ответ: 980.