Тест по теме: «Многогранники и круглые тела». Вариант 4.
Cечение конуса плоскостью, проходящей через его вершину и параллельное его основанию?
Точка; b) Отрезок; c) Круг; d) Равнобедренный треугольник.
Пирамида – это . . .
Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и
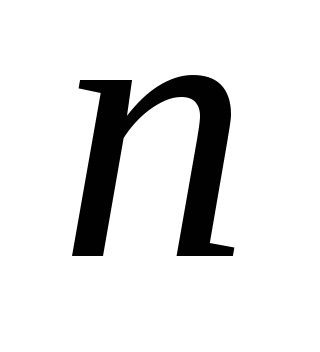 параллелограммов;
параллелограммов;Многогранник, составленный из
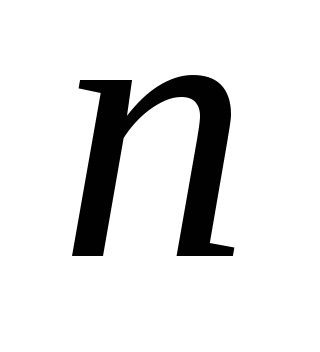 -угольника и
-угольника и 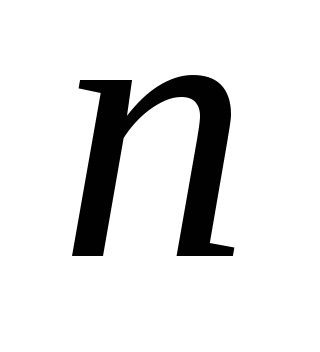 треугольников;
треугольников;Правильный многогранник, составленный из двадцати равносторонних треугольников.
Какая фигура получится в осевом сечении конуса, у которого радиус основания конуса равен половине образующей?
Равносторонний треугольник; c) Равнобедренный треугольник;
Окружность; d) Прямоугольник.
Поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки называется
Цилиндр b) Сфера c) Параллелепипед d) Конус
Какая фигура получится в осевом сечении цилиндра?
Круг; b) Треугольник; c) Прямоугольник; d)Пятиугольник.
Найдите площадь боковой поверхности правильной треугольной пирамиды, если одна из сторон основания равна 5 см, а высота составляет 3см?
15 см2 b) 30см2 c)
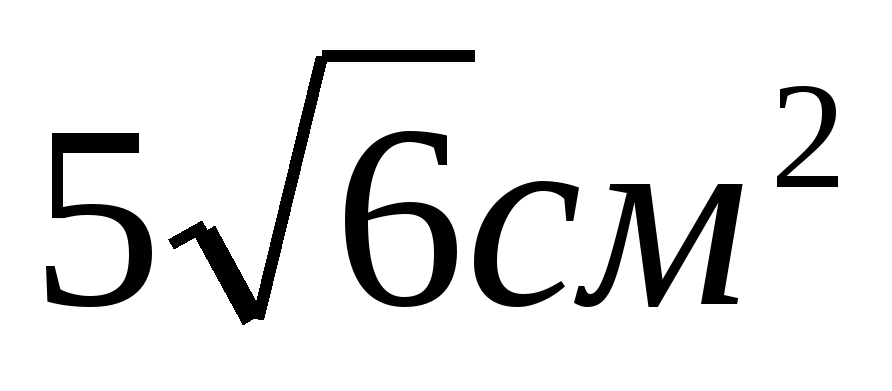 d)
d) 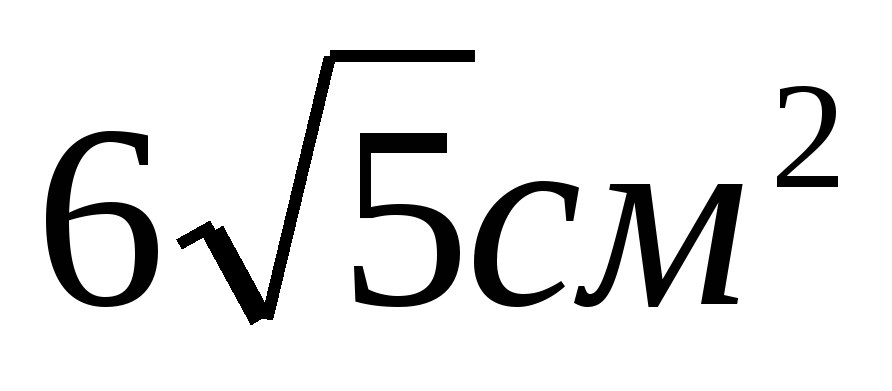
Какая из перечисленных фигур не является сечением конуса
Точка; b) Круг; c) Трапеция; d) Треугольник.
Площадь боковой поверхности цилиндра вычисляется по формуле
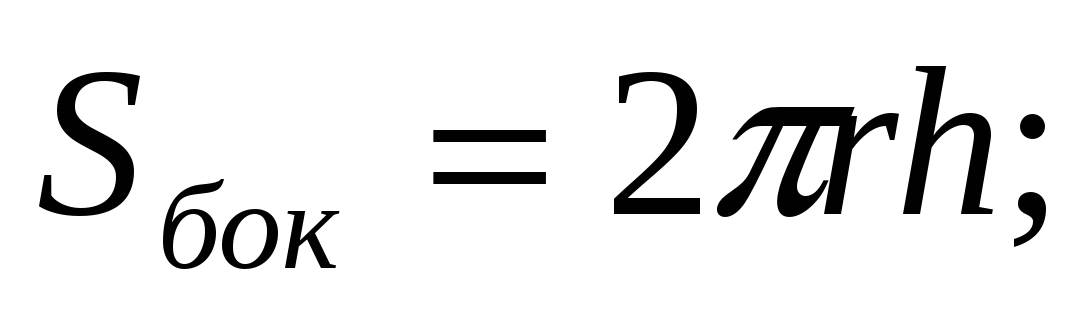 b)
b) 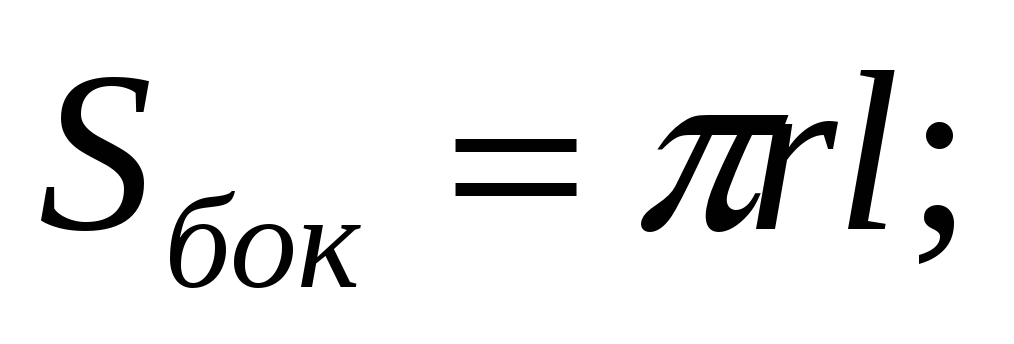 c)
c) 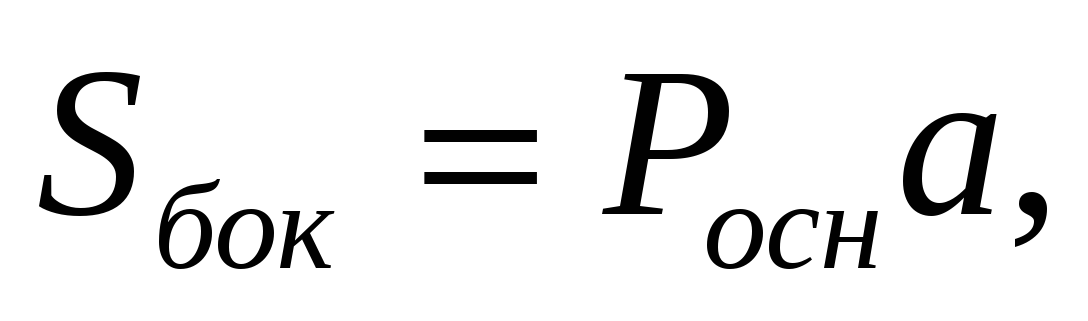 где
где  - апофема.
- апофема.
В правильной треугольной призме сторона основания равна 10 см и высота 15 см. Вычислить площадь боковой поверхности призмы.
α ) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Площадь боковой поверхности прямой призмы равна . . .
Половине произведения периметра основания на апофему;
Сумме оснований призмы умноженных на высоту призмы;
Произведению периметра основания на высоту призмы;
Произведению половины длины окружности основания на образующую.
Боковой гранью правильной пятиугольной усечённой пирамиды является . . .
Треугольник; b) квадрат; с) Равнобедренная трапеция; d) Прямоугольник.
Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ параллелепипеда.
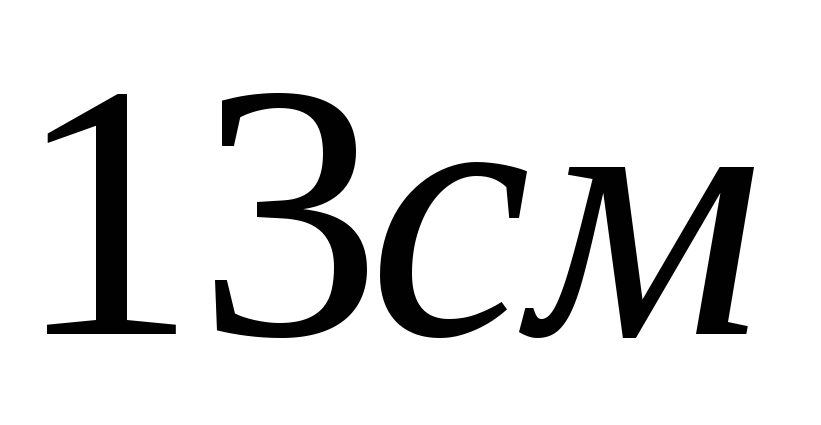 b)
b) 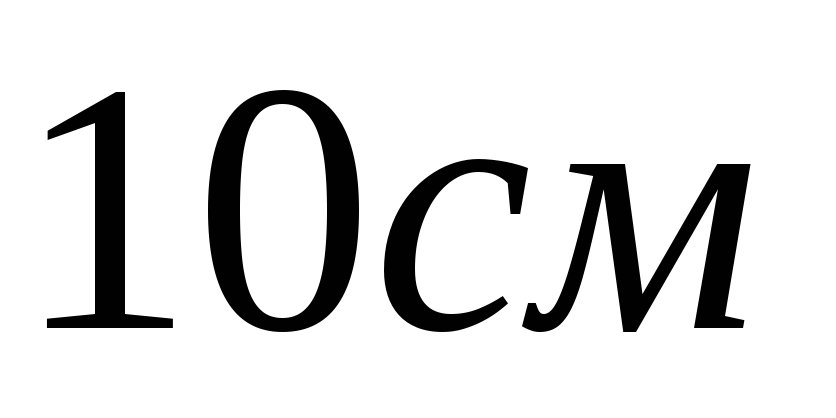 c)
c) 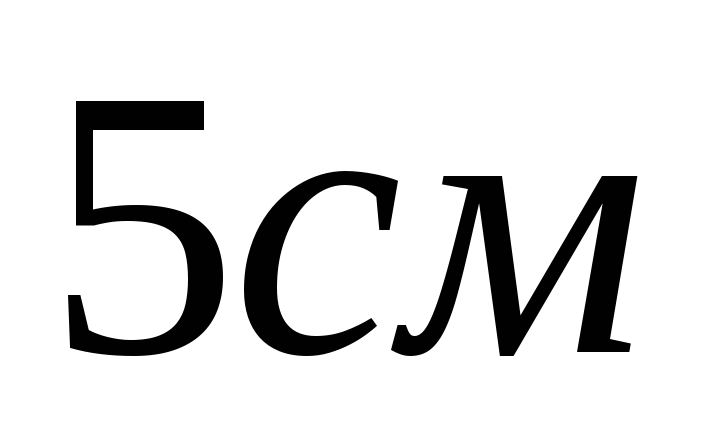 d)
d) 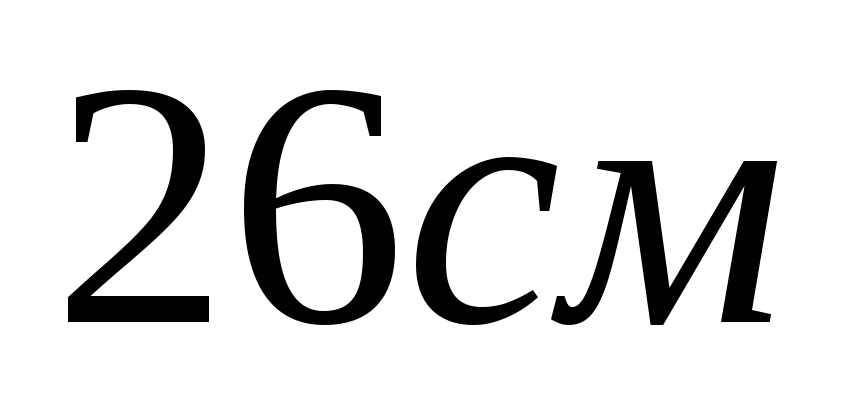
Сколько граней имеет правильная треугольная призма?
6; b) 8; c) 12; d) 9.
Найдите диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота 4 м.
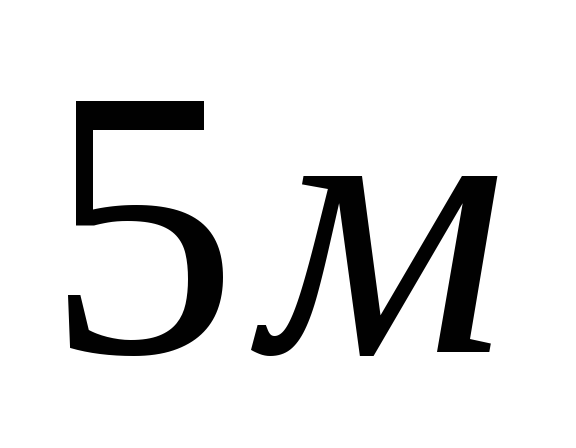 b)
b) 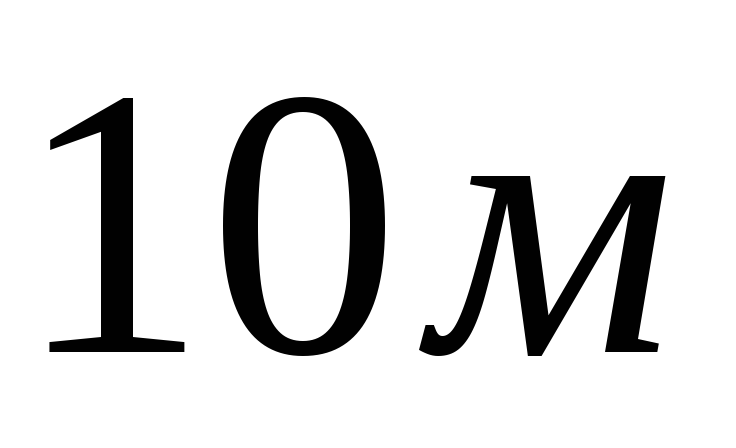 c)
c) 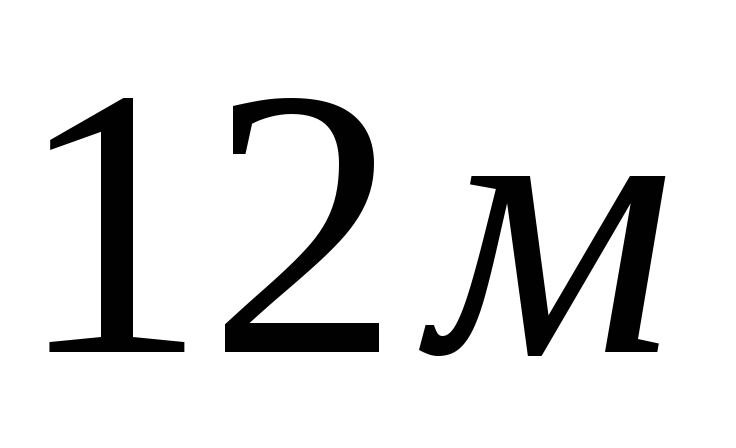 d)
d) 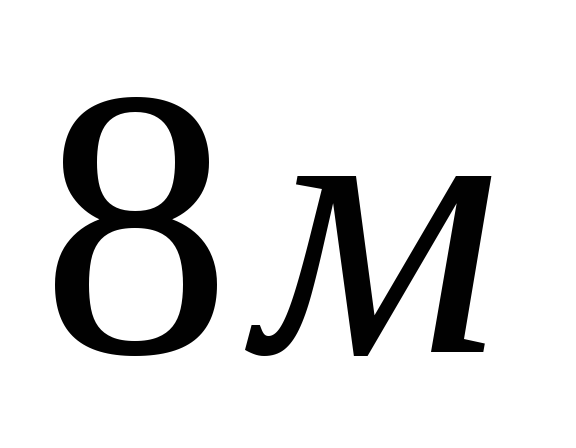
Какая фигура получиться в сечении конуса, параллельно плоскости основания?
Круг, радиус которого больше радиуса основания конуса;
Круг, радиус которого меньше радиуса основания конуса;
Круг, радиус которого равен радиусу основания конуса; d) Равнобедренный треугольник.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть . . .
Плоскостью; b) Двугранным углом; с) Гранью многогранника; d) Многогранником.
Площадь боковой поверхности правильной пирамиды равна
Произведению периметра основания на высоту призмы;
Сумме оснований призмы умноженных на высоту призмы;
Половине произведения периметра основания на апофему;
Произведению половины длины окружности основания на образующую.
Какое наименьшее число ребер может иметь многогранник?
6 b) 3 c) 8 d) 9
Тест по теме: «Многогранники и круглые тела». Вариант 3.
Конус нельзя получить путем вращения:
Прямоугольника вокруг боковой стороны; b) Равнобедренного треугольника вокруг его оси;
c) Прямоугольного треугольника вокруг катета; d) Треугольника вокруг его стороны.
Площадь боковой поверхности правильной пирамиды равна
Половине произведения периметра основания на апофему;
Сумме оснований призмы умноженных на высоту призмы;
Произведению периметра основания на высоту призмы;
Произведению половины длины окружности основания на образующую.
Боковой гранью правильной треугольной усечённой пирамиды является . . .
Треугольник; с) Равнобедренный треугольник;
Равнобедренная трапеция; d) Прямоугольник.
Найдите площадь боковой поверхности правильной треугольной призмы, если одна из сторон основания равна 5 см, а высота составляет 3см?
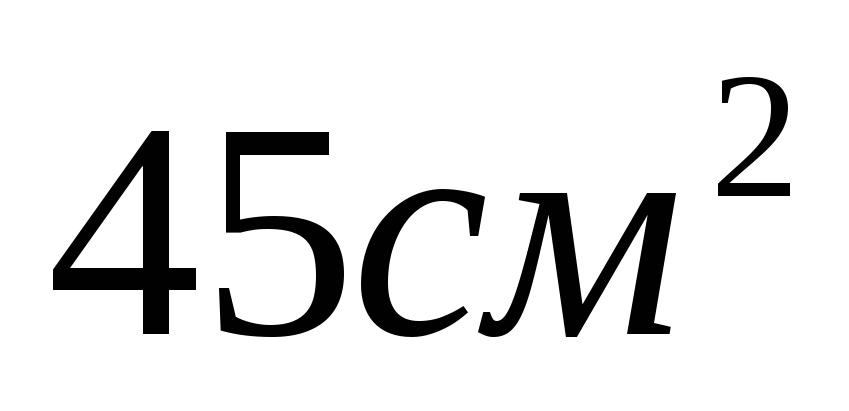 b)
b) 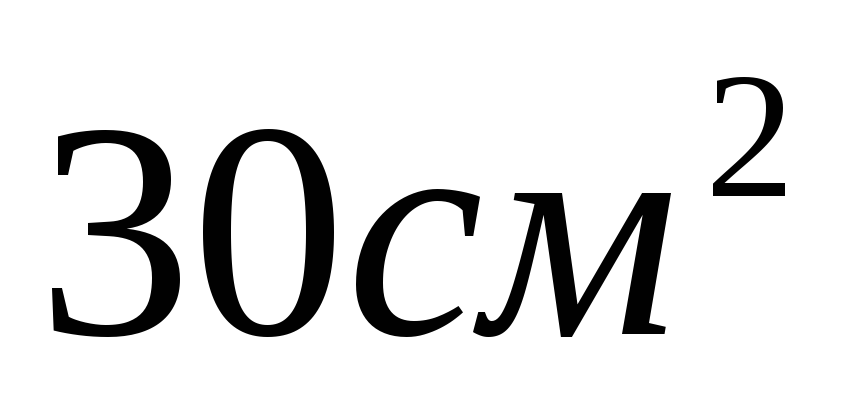 c)
c) 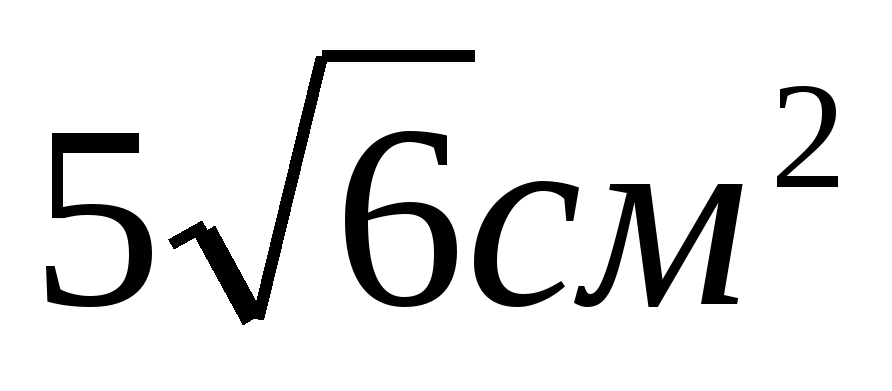 d)
d) 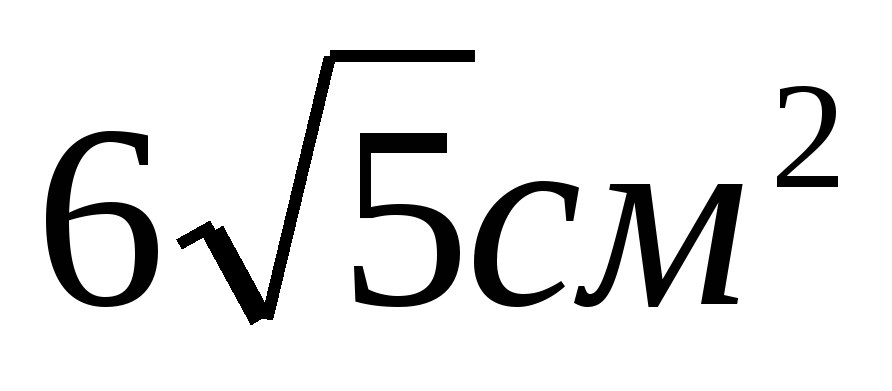
Найдите диагональ осевого сечения, если радиус цилиндра равен 3 м, а высота 8 м.
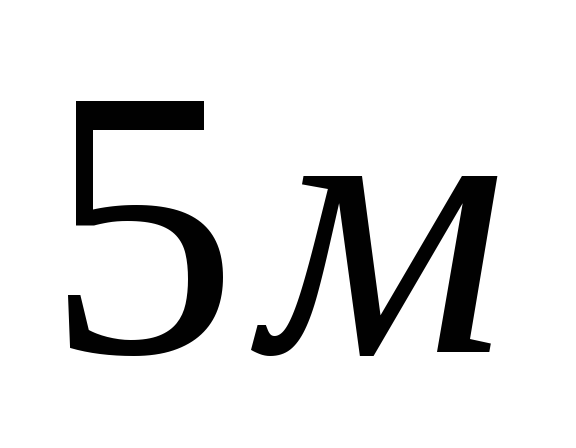 b)
b) 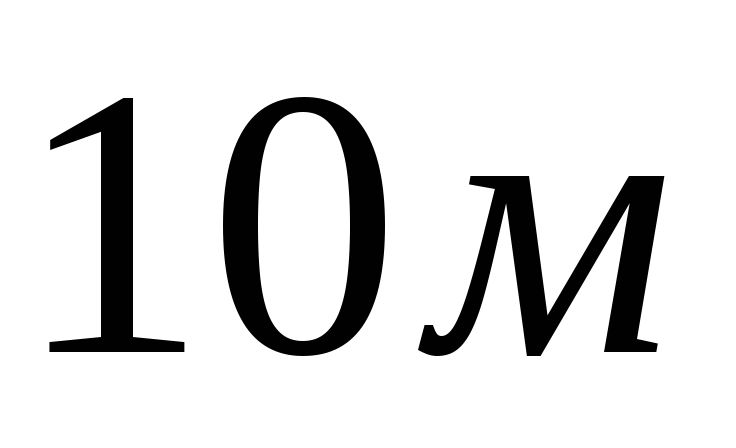 c)
c) 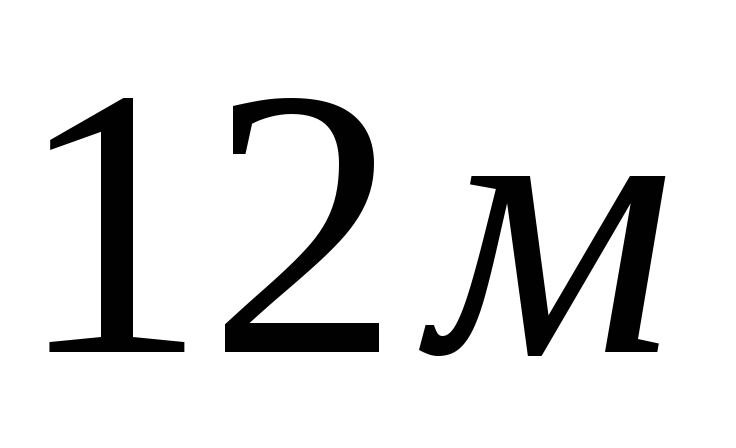 d)
d) 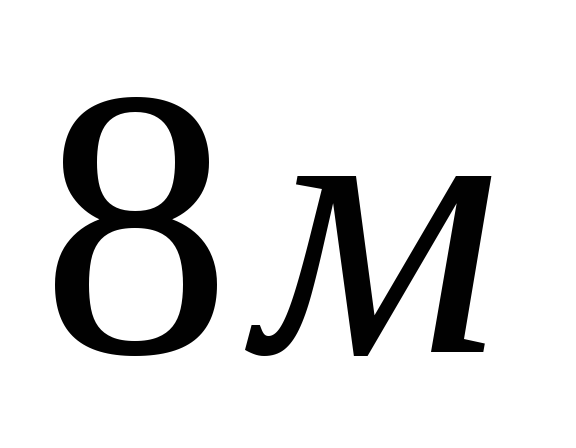
В правильной четырехугольной пирамиде сторона основания равна 5 см и высота боковой грани 15 см. Вычислить площадь боковой поверхности призмы.
225см2 b) 75см2 c) 100см2 d) 45см2
Что представляет собой сечение конуса плоскостью, проходящей через его вершину и образующую?
Отрезок; b) Круг; c) Точка; c) Равнобедренный треугольник.
Какое из перечисленных фигур не является сечением цилиндра
Круг; b) Прямоугольник; c) Треугольник; d) Ромб.
Какое наименьшее число ребер может иметь многогранник?
3 b) 9 c) 6 d) 8
Какая фигура получиться в сечении конуса, которое параллельно плоскости основания?
Круг меньшего радиуса основания конуса; б) Круг большего радиуса основания конуса;
с) Круг, радиус которого равен радиусу основания конуса; d) Равнобедренный треугольник.
Тело, ограниченное конической поверхностью и кругом с границей L, называется . . .
Конусом; b) Цилиндром; c) Параллелепипедом; d) Сферой.
Пирамида – этo: a) Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и
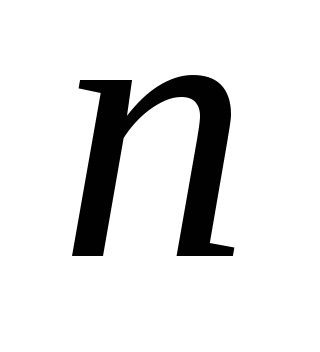 параллелограммов;
параллелограммов;
Многогранник, составленный из
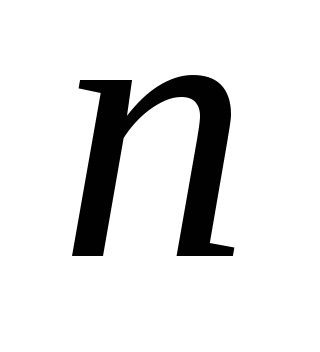 -угольника и
-угольника и 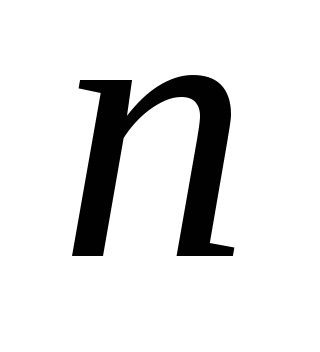 треугольников;
треугольников;Правильный многогранник, составленный из двадцати равносторонних треугольников.
Какая фигура получится в осевом сечении цилиндра?
Круг; b) Треугольник; c) Пятиугольник; d) Прямоугольник;
Диагонали параллелепипеда:
Не пересекаются; b) Не пересекаются, но численно равны;
c) Пересекаются в одной точке и делятся в этой точке пополам;
d) Пересекаются и перпендикулярны.
Основанием прямого параллелепипеда является ромб с диагоналями 3 см и 6 см, а высота параллелепипеда равна 8 см. Найдите большую диагональ параллелепипеда
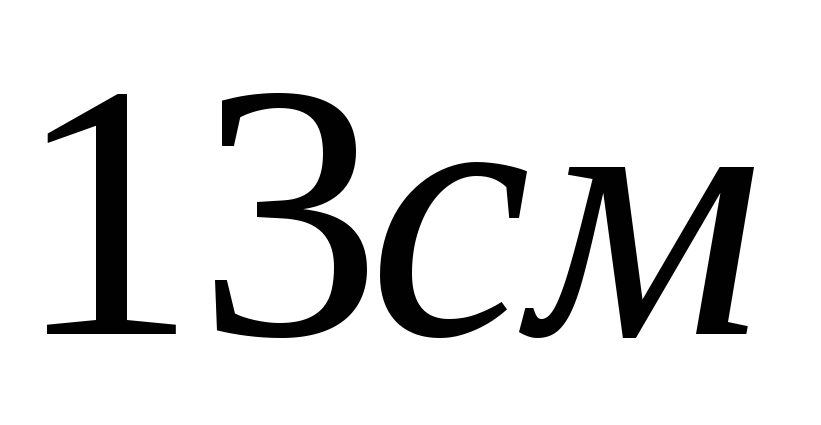 b)
b) 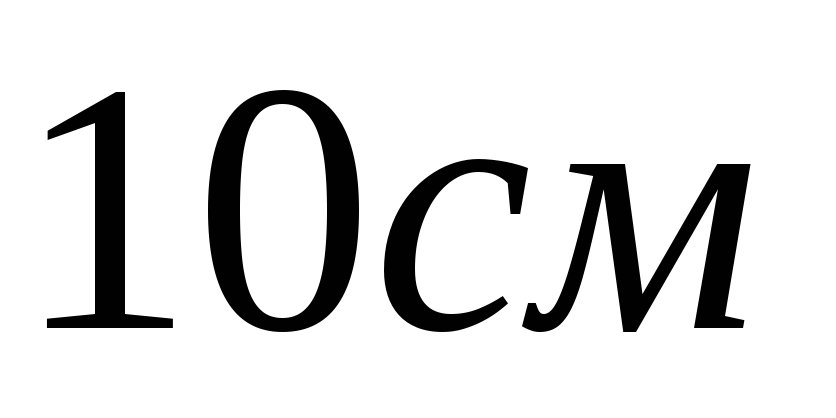 c)
c) 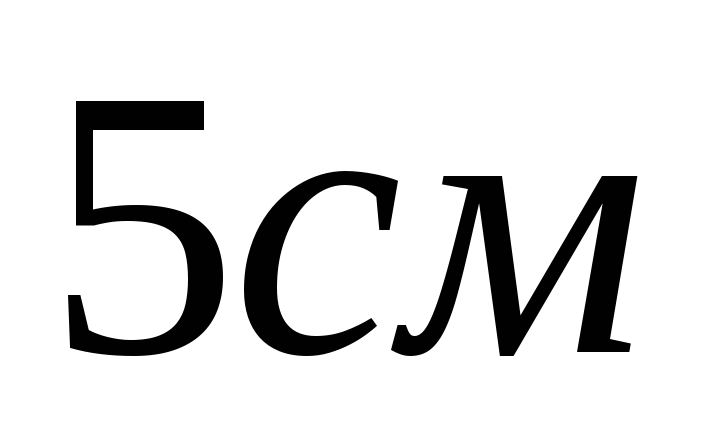 d)
d) 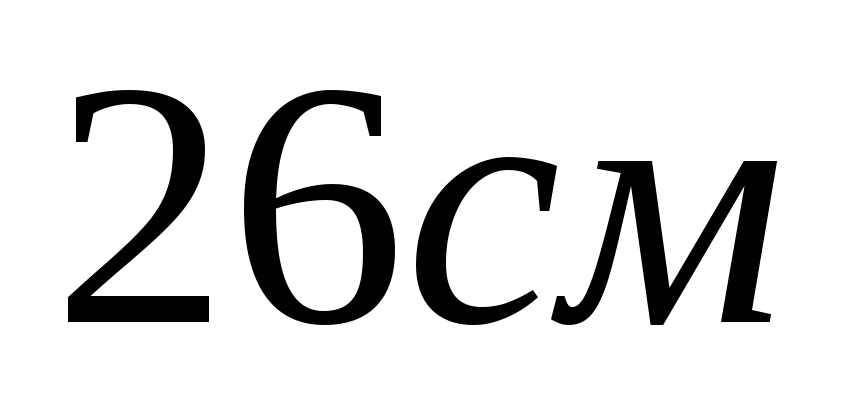
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется . . . a) Конусом; b) Цилиндром; c) Параллелепипедом; d) Сферой.
Полная поверхность пирамиды – это:
Сумма площадей всех её граней (основания и боковых граней);
Произведение основания на боковую поверхность; с) Разность боковой поверхности и основания
Цилиндр можно получить путем вращения
Прямоугольника; b) Треугольника; c) Трапеции; d) Пятиугольника.
Тест по теме: «Многогранники и круглые тела». Вариант 2.
Тело, ограниченное конической поверхностью и кругом с границей L, называется . . .
Сферой;
Цилиндром;
Параллелепипедом;
Конусом.
Основанием прямого параллелепипеда является ромб с диагоналями 6 см и 3 см, а высота параллелепипеда равна 8 см. Найдите большую диагональ параллелепипеда
Какая фигура получится в осевом сечении конуса, у которого радиус основания конуса равен половине образующей?
Равносторонний треугольник;
Равнобедренный треугольник;
Окружность;
Прямоугольник.
Какая фигура получится в сечении цилиндра, если секущая плоскость параллельна плоскостям оснований?
Прямоугольник;
Треугольник;
Круг;
Пятиугольник.
Найдите площадь боковой поверхности прямой треугольной призмы, если одна из сторон основания равна 5 см, а высота составляет 3см?
Какая фигура получиться в сечении конуса, которое параллельно плоскости основания?
Круг, радиус которого больше радиуса основания конуса;
Круг, радиус которого меньше радиуса основания конуса;
Круг, радиус которого равен радиусу основания конуса;
Равнобедренный треугольник.
Площадь боковой поверхности цилиндра вычисляется по формуле
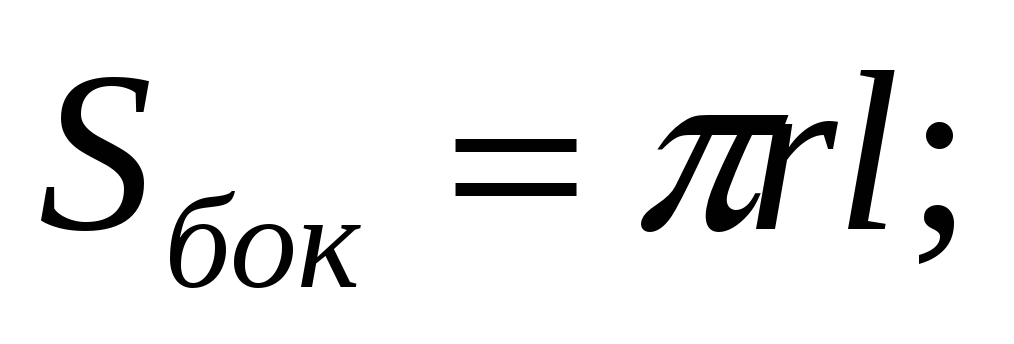
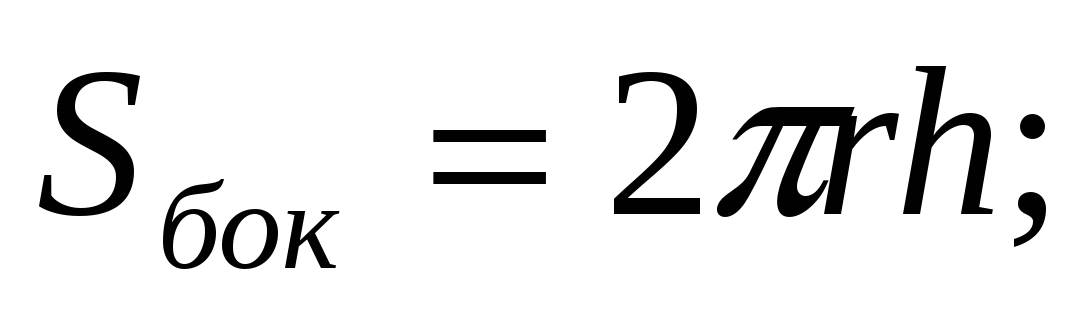
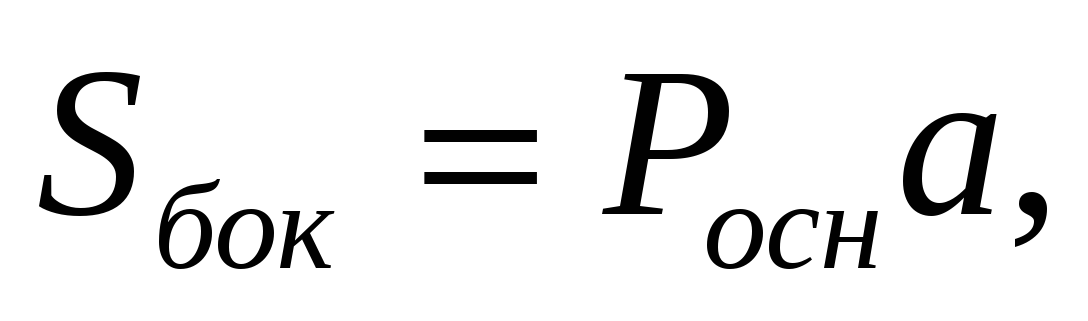 где
где  - апофема.
- апофема.
В правильной треугольной призме сторона основания равна 3 см и высота 5 см. Вычислить площадь боковой поверхности призмы.
Призма – это . . .
Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и
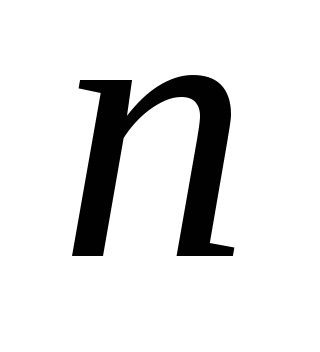 параллелограммов;
параллелограммов; Правильный многогранник, составленный из двадцати равносторонних треугольников;
Многогранник, составленный из
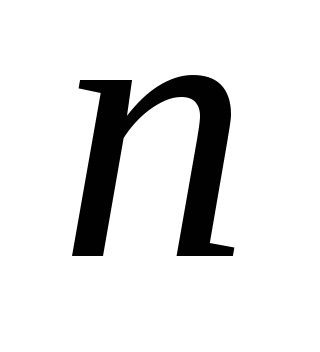 -угольника и
-угольника и 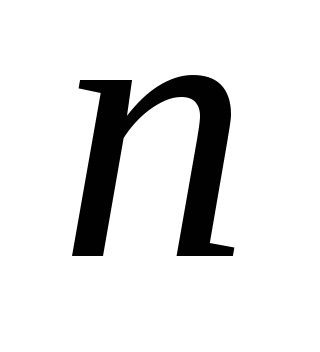 треугольников.
треугольников.
Боковой гранью правильной шестиугольной усечённой пирамиды является . . .
Треугольник;
Равнобедренный треугольник;
Равнобедренная трапеция;
Прямоугольник.
Что представляет собой сечение конуса плоскостью, проходящей через его вершину и параллельное его основанию?
Круг;
Отрезок;
Точка;
Равнобедренный треугольник.
Найдите диагональ осевого сечения, если радиус цилиндра равен 2 м, а высота 3 м.
Какая из перечисленных фигур не является сечением конуса
Точка;
Круг;
Трапеция;
Треугольник.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть . . .
Плоскостью;
Многогранником;
Гранью многогранника;
Двугранным углом.
Площадь боковой поверхности правильной пирамиды равна
Произведению периметра основания на высоту призмы;
Сумме оснований призмы умноженных на высоту призмы;
Половине произведения периметра основания на апофему;
Произведению половины длины окружности основания на образующую.
Цилиндр может получиться путем вращения
Прямоугольника;
Треугольника;
Трапеции;
Пятиугольника
Какое наименьшее число ребер может иметь многогранник?
5
6
8
9
Площадь боковой поверхности прямой призмы равна . . .
Произведению периметра основания на высоту призмы;
Сумме оснований призмы умноженных на высоту призмы;
Половине произведения периметра основания на апофему;
Произведению половины длины окружности основания на образующую.
Тест по теме: «Многогранники и круглые тела». Вариант 1.
Боковой гранью правильной пятиугольной усечённой пирамиды является . . .
Треугольник;
Равнобедренный треугольник;
Равнобедренная трапеция;
Прямоугольник.
Площадь боковой поверхности цилиндра вычисляется по формуле
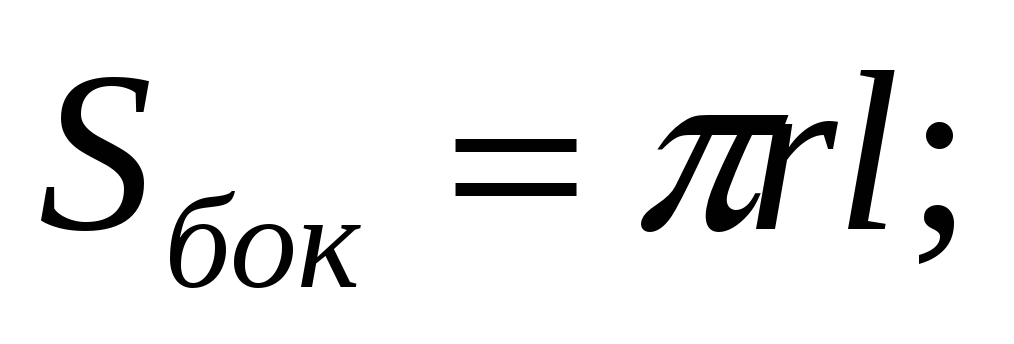
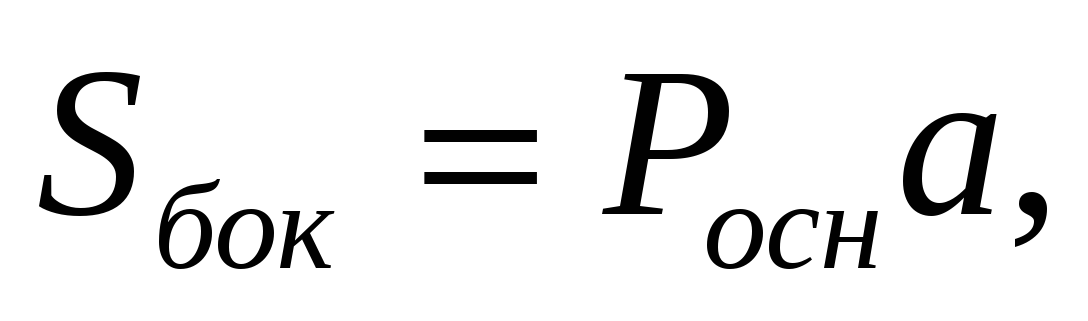 где
где  - апофема;
- апофема;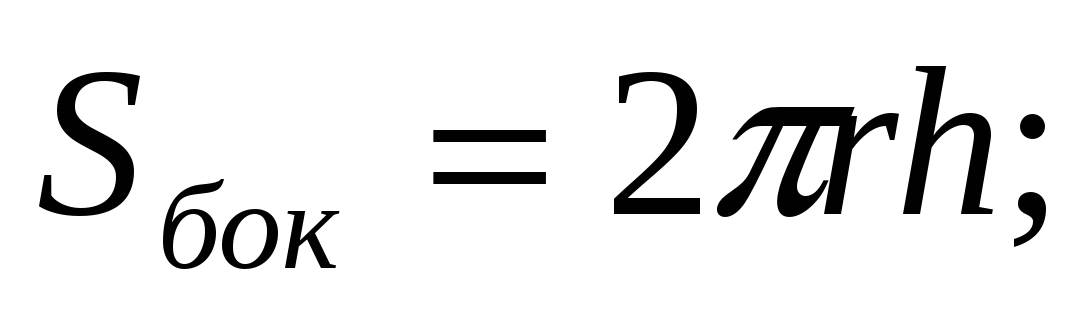
Площадь боковой поверхности правильной пирамиды равна
Произведению периметра основания на высоту призмы;
Сумме оснований призмы умноженных на высоту призмы;
Половине произведения периметра основания на апофему;
Произведению половины длины окружности основания на образующую.
В правильной треугольной призме сторона основания равна 3 см и высота 5 см. Вычислить площадь боковой поверхности призмы
Найдите диагональ осевого сечения, если радиус цилиндра равен 3 м, а высота 8 м.
Конус можно получить путем вращения . . .
Прямоугольного треугольника;
Прямоугольника;
Круга;
Пятиугольника.
Что представляет собой сечение конуса плоскостью, проходящей через его вершину и образующую?
Отрезок;
Круг;
Точка;
Равнобедренный треугольник.
Какое из перечисленных фигур не является сечением цилиндра
Круг;
Прямоугольник;
Треугольник.
Какое наименьшее число ребер может иметь многогранник?
5
7
9
6
Какая фигура получиться в сечении конуса, которое параллельно плоскости основания?
Круг, радиус которого меньше радиуса основания конуса;
Круг, радиус которого больше радиуса основания конуса;
Круг, радиус которого равен радиусу основания конуса;
Равнобедренный треугольник.
Тело, ограниченное конической поверхностью и кругом с границей L, называется . . .
Параллелепипедом;
Цилиндром;
Конусом;
Сферой.
Цилиндр можно получить путем вращения
Прямоугольника;
Треугольника;
Трапеции;
Пятиугольника.
Пирамида – это
Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и
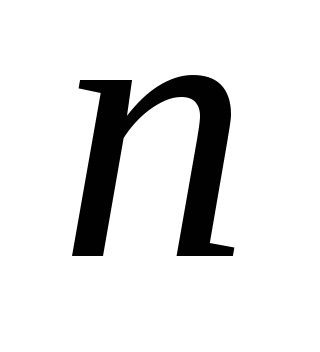 параллелограммов;
параллелограммов;Многогранник, составленный из
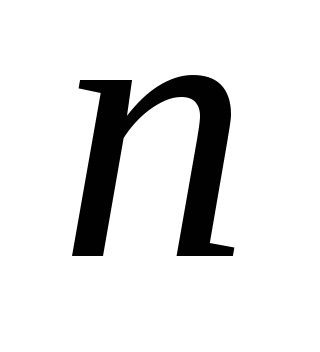 -угольника и
-угольника и 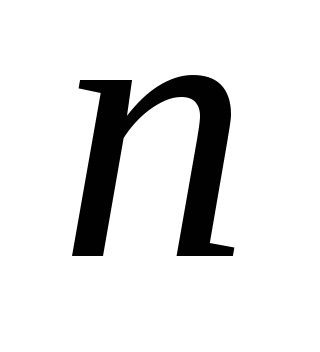 треугольников;
треугольников;Правильный многогранник, составленный из двадцати равносторонних треугольников.
Какая фигура получится в осевом сечении цилиндра?
Круг;
Треугольник;
Пятиугольник;
Прямоугольник.
Диагонали параллелепипеда . . .
Не пересекаются;
Не пересекаются, но численно равны;
Пересекаются в одной точке и делятся в этой точке пополам;
Пересекаются в одной точке и делятся в этой точке в отношении 1:3 считая от основания.
Основанием прямого параллелепипеда является ромб с диагоналями 3 см и 6 см, а высота параллелепипеда равна 4 см. Найдите меньшую диагональ параллелепипеда
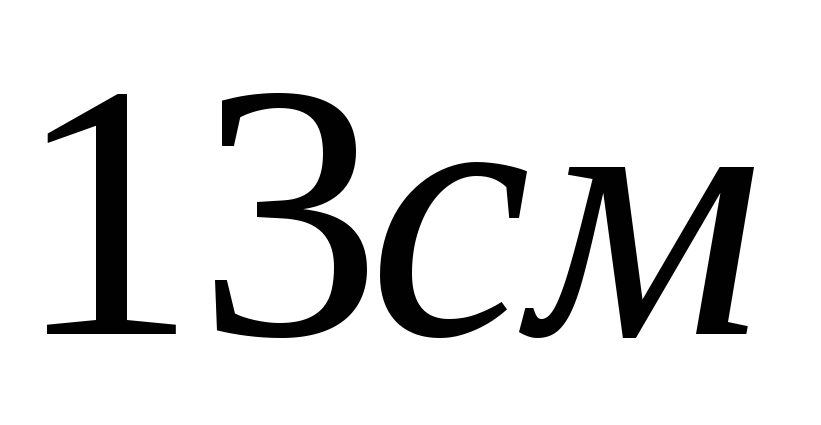 b)
b) 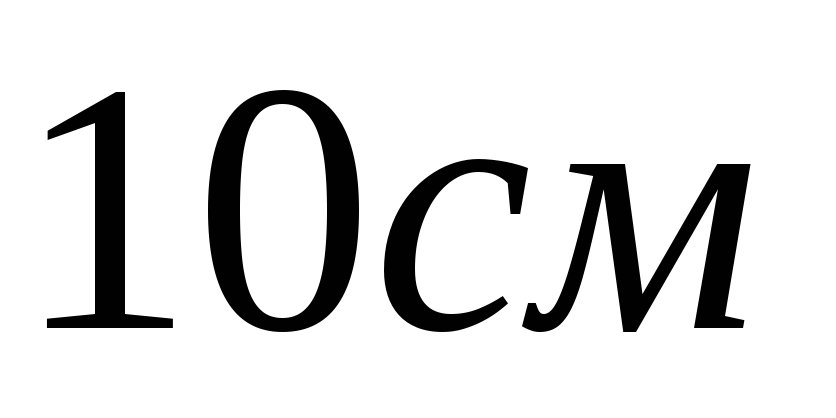 c)
c) 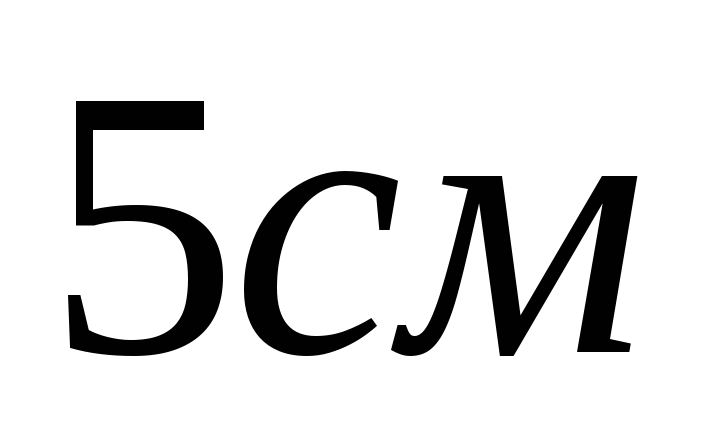 d)
d) 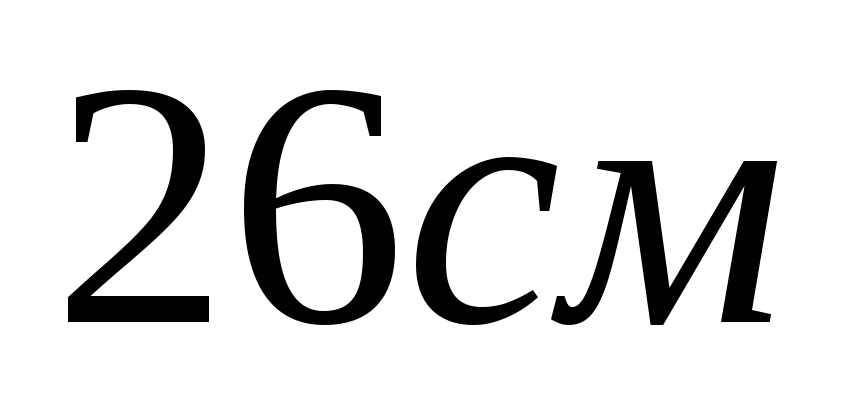
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется . . .
Конусом; b) Цилиндром; c) Параллелепипедом; d) Сферой.
Полная поверхность пирамиды – это . . .
Сумма площадей всех её граней (основания и боковых граней);
Произведение основания на боковую поверхность;
Разность боковой поверхности и основания;
Сумма площадей треугольников.
Норма оценок:
4, 5 ,16 задания оцениваются 2 – мя балами, остальные по 1 баллу
11 – 14 баллов – «3» 15 – 18 баллов - «4» 19 – 21 балл - «5»
Образовательные задачи:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.





