Проверка домашнего задания
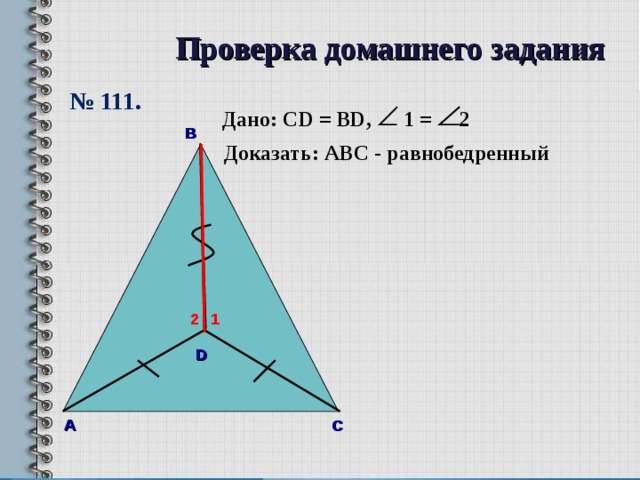
№ 111.
Дано: CD = BD , 1 = 2
В
Доказать: А B С - равнобедренный
1
2
D
А
С
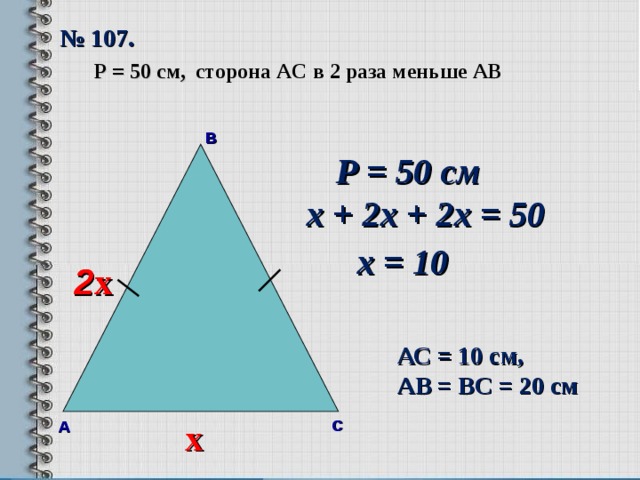
№ 107.
сторона A С в 2 раза меньше АВ
Р = 50 см,
В
Р = 50 см
х + 2х + 2х = 50
х = 10
2 х
2 х
АС = 10 см,
АВ = ВС = 20 см
х
С
А
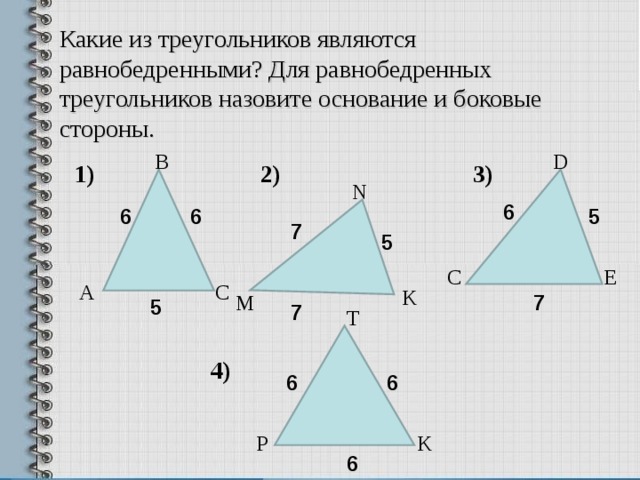
Какие из треугольников являются равнобедренными? Для равнобедренных треугольников назовите основание и боковые стороны.
D
В
2)
3)
1)
N
6
6
5
6
7
5
C
E
А
С
K
М
7
5
7
T
4)
6
6
P
K
6
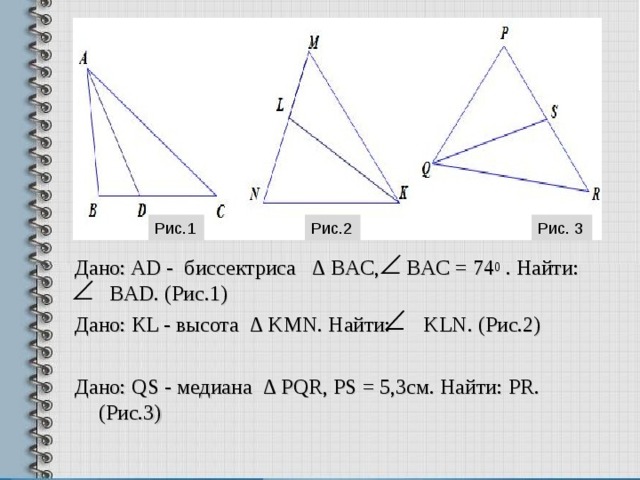
Рис. 1
Рис. 2
Рис. 3
Дано: AD - биссектриса ∆ BAC , BAC = 74 0 . Найти: BA D. (Рис.1)
Дано: КL - высота ∆ KMN. Найти: KLN . (Рис.2)
Дано: QS - медиана ∆ PQR , PS = 5,3см. Найти: PR. (Рис.3)
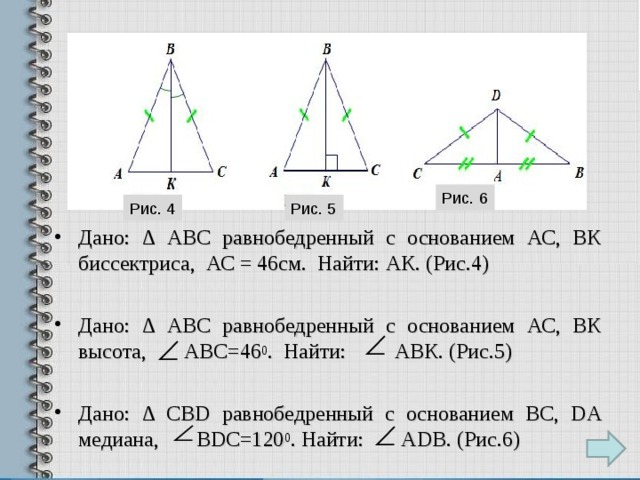
Рис. 6
Рис. 4
Рис. 5
- Дано: ∆ АВС равнобедренный с основанием АС, ВК биссектриса, АС = 46см. Найти: АК. (Рис.4)
- Дано: ∆ АВС равнобедренный с основанием АС, ВК высота, АВС=46 0 . Найти: АВК. (Рис.5)
- Дано: ∆ С BD равнобедренный с основанием B С, DA медиана, ВDС=120 0 . Найти: ADB . (Рис.6)

7 класс
Свойства равнобедренного треугольника
Три пути ведут к знанию:
Путь размышления – это путь самый благородный,
Путь подражания – это путь самый легкий,
И путь опыта – это путь самый горький.
Конфуций.
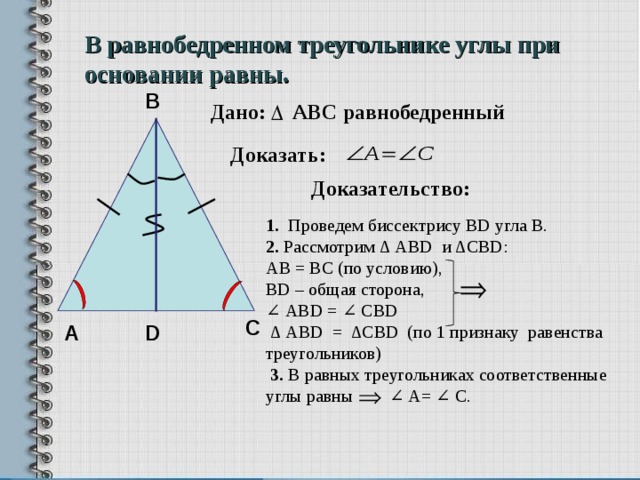
В равнобедренном треугольнике углы при основании равны.
В
Дано: АВС равнобедренный
Доказать:
Доказательство:
1. Проведем биссектрису BD угла В.
2. Рассмотрим ∆ АВ D и ∆ CBD :
AB = BC (по условию),
В D – общая сторона,
∠ А BD = ∠ С BD
∆ АВD = ∆CBD (по 1 признаку равенства треугольников)
3. В равных треугольниках соответственные углы равны ∠ А= ∠ С.
С
D
А
7
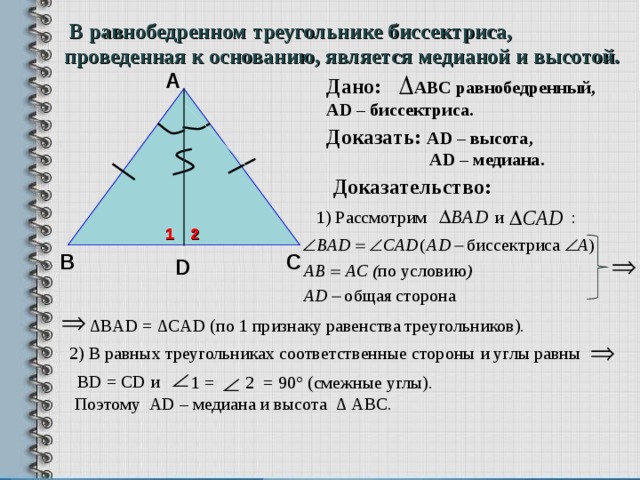
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
А
Дано: АВС равнобедренный,
А D – биссектриса .
Доказать: А D – высота,
А D – медиана.
Доказательство:
1) Рассмотрим и :
1
2
С
В
D
∆ BAD = ∆CAD ( по 1 признаку равенства треугольников).
2) В равных треугольниках соответственные стороны и углы равны
BD = CD и
1 = 2 = 90° (смежные углы).
Поэтому AD – медиана и высота ∆ АВС.
8
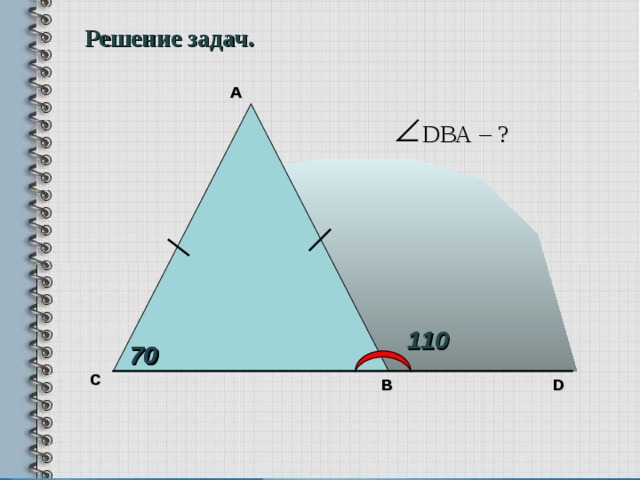
Решение задач.
А
D ВА – ?
Саврасова С.М., Ястребинецкий Г.А. «Упражнения по планиметрии на готовых чертежах»
110
70
70
С
B
D
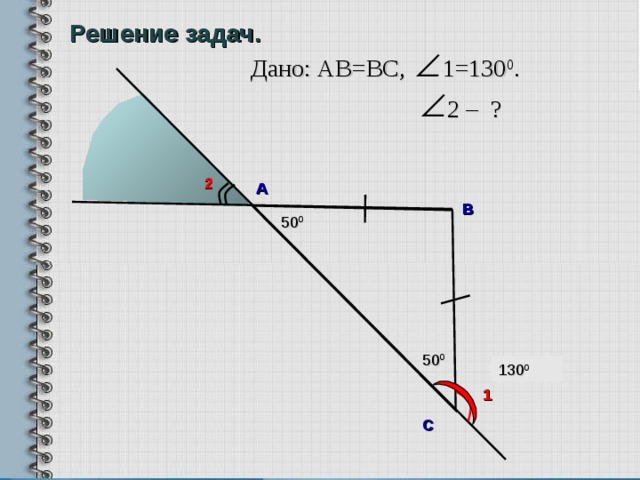
Решение задач.
Дано: АВ = В C , 1=130 0 .
2 – ?
2
А
B
50 0
Л. С. Атанасян. «Геометрия 7-9» № 112.
50 0
130 0
50 0
1
С
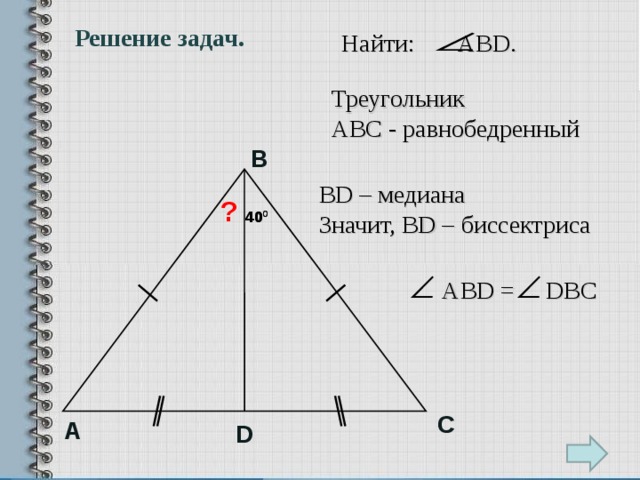
Решение задач.
Найти: АВ D .
Треугольник
АВС - равнобедренный
В
В D – медиана
Значит, В D – биссектриса
?
40 0
40 0
АВ D = D ВС
С.М. Саврасова, Г.А. Ястребинецкий «Упражнения на готовых чертежах»
С
А
D

Треугольники

Домашнее задание:
- п. 19 (стр. 35 – 36), № 109, 112, 118.





