Статья "Суммы конечные и бесконечные. Числовые ряды"

Суммы конечные и бесконечные. Числовые ряды

Первое знакомство с числовыми рядами состоялось в 9 классе при изучении арифметической прогрессии и геометрической прогрессии. Для задания этих последовательностей необходимо определить закон нахождения каждого члена последовательности, обычно записываемый в виде формулы.

Если   U₁,U₂,U₃,...,U_n,..- бесконечная последовательность чисел, то формально записанное выражение

  U₁+U₂+U₃+...+…            (1)

называется бесконечным рядом (или просто рядом). Многоточие в конце указывает, что выражение (1) не имеет последнего слагаемого, за каждым слагаемым всегда стоит следующее. Таким образом, ряд есть "бесконечная" сумма.

Короче ряд (1) можно записать в виде  ,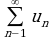

где индексы внизу и вверху символа суммы означают, что нужно взять сумму чисел U_n , когда n принимает целочисленные значения от 1 до ∞.

При сложении конечного числа слагаемых всегда получается определённый числовой результат, вычислить же сумму бесконечного числа слагаемых не может ни человек, ни компьютер, поскольку процесс сложения членов ряда (по самому определению) никогда не кончается.

Таким образом, выражение (1) является формальным, ведь сумма бесконечного числа слагаемых не определена. Но тем не менее в этом выражении поставлен знак суммирования и подразумевается, что члены ряда как-то складываются. Сумма любого конечного числа слагаемых будет найдена, если их складывать последовательно по одному. Это приводит к мысли поставить в соответствие ряду некоторое число и назвать его суммой ряда. С этой целью вводят понятие частичной суммы ряда.

Приближенные суммы ряда (1)

S₁=U₁,

S₂=U₁+U₂,

S_n=U₁+U₂+…+U_n

называются частичными суммами.

То есть, сумма n первых членов ряда называется n-й частичной суммой:

  S_n=U₁+U₂+…+U_n                           (2)

Частичные суммы имеют конечное число слагаемых, это «обычные» суммы, их можно найти, подсчитать. Для ряда получаем бесконечную последовательность его частичных сумм.

Если значения частичных сумм S_n при неограниченном возрастании n, то есть, при n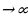  стремятся к некоторому числу S, то есть имеет предел

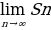       =S                                    (3)

то ряд называется сходящимся.

Это число S называется суммой ряда. В этом смысле можно записать такое равенство:

  S=U₁+U₂+…+U_n+…                                          (4)

Не для всякого ряда последовательность его частичных сумм стремится к определённому пределу.

Если предел последовательность частичных сумм ряда не существует, то ряд называется расходящимся. Расходящийся ряд суммы не имеет.