Разработка открытого урока по геометрии в 8 классе "Площади фигур"

КГУ «Ковыльненская средняя школа»

Разработка открытого урока геометрии в 8 классе по теме

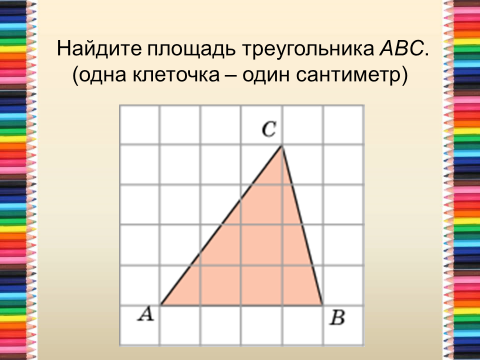
«Площади фигур»

Учитель Шут Л.А.

2016 – 2017 уч. год

Цели урока.

Обучающие:

• Закрепление у учащихся умений использовать формулы площадей.

Воспитательные:

• содействовать в развитии познавательной активности, чувства ответственности, культуры общения;

• создать условия для развития у школьников умений работать во времени;

• развивать математическую речь, творческие способности учащихся при решении геометрических задач; доказывать, сравнивать;

• совершенствовать умение применять имеющиеся знания в разных ситуациях.

Развивающие:

• содействовать в развитии логического мышления, памяти, внимания, воображения, мыслительной деятельности, процессов анализа, сравнения, обобщения.

Тип урока. Урок закрепления знаний.

Оборудование. Проектор, карточки.

Ход урока.

1. Устная работа.

Дать определение данной фигуры.

Выполнение упражнений.

1. Внутри параллелограмма АВСD отмечена точка М. Докажите, что сумма площадей треугольников АМD и ВМС равна половине площади параллелограмма.

Решение

SDВМС = h1BC, SDАМD = h2 AD, AD = BC, SDВМС + SDАМD = AD (h1 + h2) = = AD ∙ h,

S_DВМС + S_DАМD = S_ABCD.

2. В треугольнике АВС С = 90°. На сторонах АС, АВ, ВС соответственно взяты точки М, Р, K так, что четырехугольник СМРK является квадратом АС = 6 см, ВС = 14 см.

Найдите сторону МС.

Решение

1) SDАВС = AC ∙ CB = ∙ 6 ∙ 14 = 42 (см2). 2) SDАМР = AM ∙ MP = (6 – x) ∙ x (см2). 3) SDРВК = PK ∙ KB = (14 – x) ∙ x (см2).

4) S_МРСК = МС² = х².

5) S_DАВС = S_DАВР + S_DРВК + S_МРСК.

42 = (6 – х) · х + (14 – х) · х + х²

2х² + 6х – х² + 14х – х² = 84

6х + 14х = 84

х = 4,2.

Ответ: МС = 4,2 см.

Выполнение тестовых заданий (с последующей самопроверкой).

Г 8. Тест 1. В-I

1. На данном чертеже площадь всего

прямоугольника равна _________________.

1 см

1 см

2. Равные фигуры имеют равные _______________________.

3. М S_KLMNP = _________________________________

L N

K P

4. Площадь квадрата равна ______________________________________________

5. Площадь прямоугольника, смежные стороны которого равны 2,5 см и 4 см равна ______________

6. Площадь параллелограмма равна ________________________________________________________

7. В Площадь треугольника АВС, данного на чертеже

D равна ______________________________

А С

8. Площадь прямоугольного треугольника равна _____________________________________________

9. В С Формула площади трапеции АВСD, данной на чертеже,

имеет вид

S_ABCD = ­­­­­­­­­­­­­­­­­­­­­­­­_______________________

A D

Н

10. D E По данным на чертеже найти площадь параллелограмма

30˚ CDЕF.

3 4

К

C H F

8. Тест 1. В-II

1. На данном чертеже площадь всего

прямоугольника равна _________________.

1 см

1 см

2. Равные фигуры имеют равные __________________________________________________________

3. A S_ABCDEF = ________________________________________

B

F

C

E D

4. Площадь квадрата, сторона которого равна 2,5 см, равна __________________

5. Площадь прямоугольника равна _________________________________________________________

6. L M Площадь параллелограмма, данного на чертеже, равна

S_KLMN = ______________

K H N

7. Площадь треугольника равна ___________________________________________________________

8. C Площадь треугольника ABC, данного на чертеже, равна

b a S_ABC = _________

A c B

9. Площадь трапеции равна _____________________________________________________________

10 D E По данным на чертеже найти площадь ромба CDЕF.

C 4 дм F

Ответы.

1 вариант

1.

2. Площади.

3. (стороне в квадрате).

4.

5. -произведению его основания

на высоту;

-произведению двух сторон,

умноженному на синус угла

между ними;

-половине произведения

диагоналей, умноженной на

синус угла между ними.

6.

7. Половине произведения его

катетов.

8.

9. 24

2 вариант

1.

2. Площади.

3.

4. Произведению двух смежных

сторон.

5.

6. -половине произведения

основания, умноженного на

высоту, проведённую к

основанию;

-половине произведения двух

сторон, умноженной на синус

угла между ними.

7. или

8. Полусумме оснований,

умноженной на высоту.

9.

Критерии оценивания.

8-9 правильных ответов «5»

6-7 правильных ответов «4»

4-5 правильных ответа «3»

Разгадать кроссворд.

Задание на дом

Итог урока.

Самоанализ урока геометрии в 9 классе учителя математики

Шут Лидии Александровны.

Данный урок является заключительным уроком темы «Площади фигур». Урок тесно связан с предыдущими уроками данной темы, опирается на ранее изученный материал «Четырёхугольники. Соотношение между сторонами и углами прямоугольного треугольника». Урок работает на последующие, так как учит находить лощади простых фигур, что будет необходимо при изучении последующего материала.

В ходе урока были повторены формулы площадей простых фигур, продолжено развитие самостоятельности, логического мышления, применялись технические средства обучения (компьютер).

Выбранная мною структура урока и его содержание рациональны для решения поставленных задач.

Урок начинается организационным моментом, на котором учащимся сообщается тема и цели урока. Далее следует повторение материала предыдущих уроков посредством устной фронтальной работы с классом (презентация). На данном этапе урока были предложены разнообразные задания, задания на развитие логического мышления учащихся, задания, заставляющие учащихся грамотно применять полученные ранее знания, заставляющие учащихся мыслить творчески и активизируют познавательную деятельность.

Далее решение задач у доски с комментарием. Были разобраны задачи разного уровня, причём первая задача была более простая, чем вторая. Что позволило учащимся работать в нарастающем темпе.

Далее осуществляется контроль знаний, полученных на предыдущих уроках и повторенных в результате устной работы. Контроль знаний осуществляется при помощи работы над тестом с последующей самопроверкой.

Учащиеся работают в индивидуальном темпе.

Работа над кроссвордом – следующий этап урока.

Создаётся проблемная ситуация по правильному заполнению вертикалей и горизонталей. На данном этапе важно дать возможность высказаться каждому учащемуся и принять мнение каждого, и вместе сделать вывод. Этого удалось добиться фронтально работая с классом, учащиеся принимают участие в разгадывании кроссворда, «подсказывая» учителю ранее изученные факты, что позволяет им активно включиться в работу.

Все поставленные цели были реализованы на уроке. Повторение и усвоение знаний учащимися осуществлялось как через индивидуальную самостоятельную работу, так и фронтальную работу. На уроке царила доброжелательная атмосфера, высокая работоспособность учащихся обеспечивалась за счёт того, что осуществлялся личностно-ориентированный подход, шло формирование и развитие умений и навыков.