| |
РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ 10 КЛАСС
на 2017-2018 учебный год
ФГОС СОО
Рабочая программа по математике для 10 класса составлена в соответствии с Федеральным государственным образовательным стандартом среднего общего образования, утверждённым Приказом Минобрнауки РФ от 17 мая 2012 года № 413 (с изменениями и дополнениями), на основе Примерной основной образовательной программы среднего общего образования, Основной образовательной программы среднего общего образования БОУ г. Омска « Гимназия № 69 им. Чередова И.М.», авторской программы «Математика: алгебра и начала математического анализа, геометрия 10-11 класс» под редакцией Т.А.Бурмистрова, М.: «Просвещение», 2016г., 2018г. Рабочая программа конкретизирует содержание предметных тем образовательного стандарта, даёт распределение учебных часов по разделам и темам.
Алгебра и начала математического анализа. Всего 136 часов; в неделю 4 часа.
Геометрия. Всего 68 часов; в неделю 2 часа.
Описание места учебного предмета в учебном плане
Математика: алгебра и начала математического анализа, геометрия изучается на уровне среднего общего образования в качестве обязательного учебного предмета.
Рабочая программа ориентирована на использование: УМК для 10 класса:
1. Алгебра и начала математического анализа 10-11.Ш.А.Алимов, Ю.М.Колягин и др. Москва «Просвещение», 2017г.
2.Геометрия 10 – 11. Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Москва «Просвещение», 2016г.
Изучение учебного предмета «Математика: алгебра и начала математического анализа, геометрия» на углубленном уровне предполагает ориентировку на получение для подготовки специалистов инженерно-технического профиля и кадров для нужд науки.
На углубленном уровне:
- Выпускник научится в 10 классе: для успешного продолжения образования по специальностям, связанным с прикладным использованием математики.
- Выпускник получит возможность научиться в 10 классе: для обеспечения возможности успешного продолжения образования по специальностям, связанным с осуществлением научной и исследовательской деятельности в области математики и смежных наук.
Планируемые результаты освоения учебного предмета, курса
Личностные результаты:
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, основанного на диалоге культур, а также различных форм общественного сознания, осознание своего места в поликультурном мире;
сформированность основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовность и способность к самостоятельной, творческой и ответственной деятельности;
толерантное сознание и поведение в поликультурном мире, готовность и способность вести диалог с другими людьми, достигать в нём взаимопонимания, находить общие цели и сотрудничать для их достижения;
навыки сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
нравственное сознание и поведение на основе усвоения общечеловеческих ценностей;
готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
эстетическое отношение к миру, включая эстетику быта, научного и технического творчества, спорта, общественных отношений;
осознанный выбор будущей профессии и возможностей реализации собственных жизненных планов;
отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем.
Метапредметные результаты:
умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
умение использовать средства информационных и коммуникационных технологий (далее - ИКТ) в решении когнитивных, коммуникативных и организационных задач с соблюдением требований эргономики, техники безопасности, гигиены, ресурсосбережения, правовых и этических норм, норм информационной безопасности;
умение самостоятельно оценивать и принимать решения, определяющие стратегию поведения, с учётом гражданских и нравственных ценностей;
владение языковыми средствами - умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.
Предметные результаты:
сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
сформированность представлений об основных понятиях, идеях и методах математического анализа;
владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
владение навыками использования готовых компьютерных программ при решении задач;
сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;
сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения' их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;
сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.
| Раздел | Выпускник научится | Выпускник получит возможность научиться |
| Числа и выражения | 1.Свободно оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, иррациональное число, корень степени n, действительное число, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел. 2.Сравнивать действительные числа разными способами; упорядочивать числа, записанные в виде обыкновенной и десятичной дроби, числа, записанные с использованием арифметического квадратного корня, корней степени больше 2. 3.Выполнять вычисления и преобразования выражений, содержащих действительные числа, в том числе корни натуральных степеней. 4.Выполнять стандартные тождественные преобразования тригонометрических, логарифмических, степенных, иррациональных выражений. | 1.Свободно выполнять тождественные преобразования тригонометрических, логарифмических, степенных выражений.
|
| Уравнения и неравенства
| 1.Свободно оперировать понятиями: уравнение, неравенство, равносильные уравнения и неравенства, уравнение, являющееся следствием другого уравнения, уравнения, равносильные на множестве, равносильные преобразования уравнений. 2.Решать разные виды уравнений и неравенств и их систем, в том числе некоторые уравнения 3-й и 4-й степеней, дробно-рациональные и иррациональные. 3.Овладеть основными типами показательных, логарифмических, иррациональных, степенных уравнений и неравенств и стандартными методами их решений и применять их при решении задач. 4.Понимать смысл теорем о равносильных и неравносильных преобразованиях уравнений и уметь их доказывать. 5.Владеть методами решения уравнений, неравенств и их систем, уметь выбирать метод решения и обосновывать свой выбор. 6.Использовать метод интервалов для решения неравенств, в том числе дробно-рациональных и включающих в себя иррациональные выражения. 7.Владеть разными методами доказательства неравенств; 8.Свободно использовать тождественные преобразования при решении уравнений и систем уравнений. | 1.Свободно определять тип и выбирать метод решения показательных и логарифмических уравнений и неравенств, иррациональных уравнений и неравенств, тригонометрических уравнений и неравенств, их систем. 2.Свободно решать системы линейных уравнений.
|
| Функции | 1.Владеть понятием степенная функция; строить ее график и уметь применять свойства степенной функции при решении задач. 2.Владеть понятиями показательная функция, экспонента; строить их графики и уметь применять свойства показательной функции при решении задач. 3.Владеть понятием логарифмическая функция; строить ее график и уметь применять свойства логарифмической функции при решении задач. 4.Владеть понятиями тригонометрические функции; строить их графики и уметь применять свойства тригонометрических функций при решении задач. 5.Владеть понятием обратная функция; применять это понятие при решении задач. | Владеть понятием асимптоты и уметь его применять при решении задач.
|
| Элементы математического анализа | 1.Владеть понятием бесконечно убывающая геометрическая прогрессия и уметь применять его при решении задач. | В повседневной жизни и при изучении других учебных предметов: 1.Решать прикладные задачи из биологии, физики, химии, экономики и других предметов, связанные с исследованием характеристик реальных процессов, нахождением наибольших и наименьших значений, скорости и ускорения и т.п. 2.Интерпретировать полученные результаты. |
| Геометрия | 1.Владеть геометрическими понятиями при решении задач и проведении математических рассуждений. 2.Самостоятельно формулировать определения геометрических фигур, выдвигать гипотезы о новых свойствах и признаках геометрических фигур и обосновывать или опровергать их, обобщать или конкретизировать результаты на новых классах фигур, проводить в несложных случаях классификацию фигур по различным основаниям. 3.Исследовать чертежи, включая комбинации фигур, извлекать, интерпретировать и преобразовывать информацию, представленную на чертежах. 4.Решать задачи геометрического содержания, в том числе в ситуациях, когда алгоритм решения не следует явно из условия, выполнять необходимые для решения задачи дополнительные построения, исследовать возможность применения теорем и формул для решения задач. 5.Уметь формулировать и доказывать геометрические утверждения. 6.Владеть понятиями стереометрии: призма, параллелепипед, пирамида, тетраэдр. 7.Иметь представления об аксиомах стереометрии и следствиях из них и уметь применять их при решении задач. 8.Уметь строить сечения многогранников с использованием различных методов, в том числе и метода следов. 9.Иметь представление о скрещивающихся прямых в пространстве и уметь находить угол и расстояние между ними. 10.Применять теоремы о параллельности прямых и плоскостей в пространстве при решении задач. 11.Уметь применять параллельное проектирование для изображения фигур. 12.Уметь применять перпендикулярности прямой и плоскости при решении задач. 13.Владеть понятиями ортогональное проектирование, наклонные и их проекции, уметь применять теорему о трех перпендикулярах при решении задач. 14.Владеть понятиями расстояние между фигурами в пространстве, общий перпендикуляр двух скрещивающихся прямых и уметь применять их при решении задач. 15.Владеть понятием угол между прямой и плоскостью и уметь применять его при решении задач. 16.Владеть понятиями двугранный угол, угол между плоскостями, перпендикулярные плоскости и уметь применять их при решении задач. 17.Владеть понятиями призма, параллелепипед и применять свойства параллелепипеда при решении задач. 18.Владеть понятием прямоугольный параллелепипед и применять его при решении задач. 19.Владеть понятиями пирамида, виды пирамид, элементы правильной пирамиды и уметь применять их при решении задач. 20.Иметь представление о теореме Эйлера, правильных многогранниках. 21.Уметь применять для решения задач свойства плоских и двугранных углов трехгранного угла, теоремы косинусов и синусов трехгранного угла.
| 1.Иметь представление об аксиоматическом методе. 2.Владеть понятием геометрические места точек в пространстве и уметь применять их для решения задач. 3.Уметь применять для решения задач свойства плоских и двугранных углов, трехгранного угла, теоремы косинусов и синусов для трехгранного угла. 4.Владеть понятием перпендикулярное сечение призмы и уметь применять его при решении задач. 5.Иметь представление о двойственности правильных многогранников. 6.Владеть понятиями центральное и параллельное проектирование и применять их при построении сечений многогранников методом проекций.
|
| История математики
| 1.Иметь представление о вкладе выдающихся математиков в развитие науки. 2.Понимать роль математики в развитии России. | Представлять вклад выдающихся математиков в развитие математики и иных научных областей; понимать роль математики в развитии России.
|
| Методы математики | 1.Использовать основные методы доказательства, проводить доказательство и выполнять опровержение. 2.Применять основные методы решения математических задач. 3.На основе математических закономерностей в природе характеризовать красоту и совершенство окружающего мира и произведений искусства. 4.Применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач. 5.Пользоваться прикладными программами и программами символьных вычислений для исследования математических объектов. | Применять математические знания к исследованию окружающего мира (моделирование физических процессов, задачи экономики).
|
Содержание учебного предмета, курса
Алгебра и начала математического анализа.
Арифметический корень натуральной степени. Степень с действительным показателем, свойства степени. Степенная функция и ее свойства и график. Взаимно обратные функции. Графики взаимно обратных функций. Иррациональные уравнения. Иррациональные неравенства.
Показательная функция и ее свойства и график. Простейшие показательные уравнения и неравенства.
Логарифмическая функция и ее свойства и график. Логарифм, свойства логарифма. Десятичный и натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Число e и функция y= e
. Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических и иррациональных неравенств.
Радианная мера угла, тригонометрическая окружность. Тригонометрические функции чисел и углов. Формулы приведения, сложения тригонометрических функций, формулы двойного и половинного аргумента. Преобразование суммы, разности в произведение тригонометрических функций, и наоборот.
Тригонометрические уравнения cosx=а, sinx=а, tgx=а, Однородные тригонометрические уравнения. Решение простейших тригонометрических неравенств. Простейшие системы тригонометрических уравнений.
Геометрия.
Основные понятия геометрии в пространстве. Аксиомы стереометрии и следствия из них. Понятие об аксиоматическом методе.
Теорема Менелая для тетраэдра. Построение сечений многогранников методом следов. Центральное проектирование. Построение сечений многогранников методом проекций.
Скрещивающиеся прямые в пространстве. Угол между ними. Методы нахождения расстояний между скрещивающимися прямыми.
Теоремы о параллельности прямых и плоскостей в пространстве. Параллельное проектирование и изображение фигур. Геометрические места точек в пространстве.
Перпендикулярность прямой и плоскости. Ортогональное проектирование. Наклонные и проекции. Теорема о трех перпендикулярах.
Расстояния между фигурами в пространстве. Общий перпендикуляр двух скрещивающихся прямых. Методы нахождения расстояний между скрещивающимися прямыми.
Углы в пространстве. Перпендикулярные плоскости. Трехгранный и многогранный угол. Свойства плоских углов многогранного угла. Свойства плоских и двугранных углов трехгранного угла. Теоремы косинусов и синусов для трехгранного угла.
Виды многогранников. Правильные многогранники. Развертки многогранника. Кратчайшие пути на поверхности многогранника.
Теорема Эйлера. Двойственность правильных многогранников.
Призма. Параллелепипед. Свойства параллелепипеда. Прямоугольный параллелепипед. Наклонные призмы. Площадь ортогональной проекции. Перпендикулярное сечение призмы.
Пирамида. Виды пирамид. Элементы правильной пирамиды. Пирамиды с равнонаклоненными ребрами и гранями, их основные свойства.
Виды тетраэдров. Ортоцентрический тетраэдр, каркасный тетраэдр, равногранный тетраэдр. Прямоугольный тетраэдр. Медианы и бимедианы тетраэдра. Достраивание тетраэдра до параллелепипеда.
Тематическое планирование с указанием количества часов, отводимых на освоение каждой темы
| № пункта (геометрия)или параграфа (алгебра) | Наименование глав и параграфов | Количество часов | Дата |
|
| |||
|
| |||
|
| Глава 1. Действительные числа. | 18 |
|
| §1 | Целые и рациональные числа. | 2 |
|
| §2 | Действительные числа. | 2 |
|
| §3 | Бесконечно убывающая геометрическая прогрессия. | 2 |
|
| §4 | Арифметический корень натуральной степени. | 4 |
|
| §5 | Степень с рациональным показателем. | 5 |
|
|
| Урок обобщения и систематизации знаний. | 2 |
|
|
| Контрольная работа №1 по теме «Действительные числа». | 1 |
|
|
| Глава 2. Степенная функция. | 18 |
|
| §6 | Степенная функции, её свойства и график. Работа над ошибками. | 3 |
|
| §7 | Взаимно обратные функции. | 2 |
|
| §8 | Равносильные уравнения и неравенства. | 4 |
|
| §9 | Иррациональные уравнения. | 4 |
|
|
| Входная контрольная работа | 1 |
|
| §10 | Иррациональные неравенства. Работа над ошибками. | 2 |
|
|
| Урок обобщения и систематизации знаний. | 2 |
|
|
| Контрольная работа №2 по теме «Степенная функция». | 1 |
|
|
| Глава 3. Показательная функция. | 12 |
|
| §11 | Показательная функция, её свойства и график. Работа над ошибками | 2 |
|
| §12 | Показательные уравнения. | 3 |
|
| §13 | Показательные неравенства. | 3 |
|
| §14 | Системы показательных уравнений и неравенств. | 2 |
|
|
| Урок обобщения и систематизации знаний. | 1 |
|
|
| Контрольная работа №3 по теме «Показательная функция». | 1 |
|
|
| Глава 4. Логарифмическая функция. | 19 |
|
| §15 | Логарифмы. Работа над ошибками. | 2 |
|
| §16 | Свойства логарифмов. | 2 |
|
| §17 | Десятичные и натуральные логарифмы. Формула перехода. | 3 |
|
|
| Контрольная работа за 1 полугодие(алгебра + геометрия) | 2 |
|
| §18 | Логарифмическая функция, её свойства и график. | 2 |
|
| §19 | Логарифмические уравнения. | 3 |
|
| §20 | Логарифмические неравенства. | 4 |
|
|
| Урок обобщения и систематизации знаний. | 2 |
|
|
| Контрольная работа № 4 по теме «Логарифмическая функция». | 1 |
|
|
| Глава 5. Тригонометрические формулы. | 27 |
|
| §21 | Радианная мера угла. Работа над ошибками. | 1 |
|
| §22 | Поворот точки вокруг начала координат. | 2 |
|
| §23 | Определение синуса, косинуса и тангенса угла. | 2 |
|
| §24 | Знаки синуса, косинуса и тангенса угла. | 1 |
|
| §25 | Зависимость между синусом, косинусом и тангенсом одного и того же угла. | 2 |
|
| §26 | Тригонометрические тождества. | 3 |
|
| §27 | Синус, косинус и тангенс углов | 1 |
|
| §28 | Формулы сложения. | 3 |
|
| §29 | Синус, косинус и тангенс двойного угла. | 2 |
|
| §30 | Синус, косинус и тангенс половинного угла. | 2 |
|
| §31 | Формулы привидения. | 2 |
|
| §32 | Сумма и разность синусов. Сумма и разность косинусов. | 3 |
|
|
| Урок обобщения и систематизации знаний. | 2 |
|
|
| Контрольная работа №5 по теме «Основные тригонометрические формулы». | 1 |
|
|
| Глава 6. Тригонометрические уравнения. | 18 |
|
| §33 | Уравнение | 3 |
|
| §34 | Уравнение | 3 |
|
| §35 | Уравнение | 2 |
|
| §36 | Решение тригонометрических уравнений. | 5 |
|
|
| Примеры решения простейших тригонометрических неравенств | 2 |
|
|
| Урок обобщения и систематизации знаний. | 2 |
|
|
| Контрольная работа №6 по теме «Тригонометрические уравнения». | 1 |
|
|
| Итоговое повторение. | 22-10а,21-10б |
|
|
| Повторение по теме «Действительные числа». | 3 |
|
|
| Повторение по теме «Степенная функция». | 4 |
|
|
| Повторение по теме «Показательная функция». | 4 |
|
|
| Контрольная работа за год (алгебра + геометрия) | 2 |
|
|
| Повторение по теме «Логарифмическая функция». | 2 |
|
|
| Повторение по теме «Основные тригонометрические формулы». | 3-10а,4-10б |
|
|
| Повторение по теме «Тригонометрические уравнения». | 4-10а,5-10б |
|
|
| Глава8. Некоторые сведения из планиметрии. | 12 |
|
|
| §1.Углы и отрезки, связанные с окружностью. | 4 |
|
|
| §2.Решение треугольников. | 4 |
|
|
| §3.Теоремы Менелая и Чевы | 2 |
|
|
| §4.Эллипс, гипербола и парабола | 2 |
|
|
| Введение | 3 |
|
| 1,2 | Предмет стереометрии. Аксиомы стереометрии. | 1 |
|
| 3 | Некоторые следствия из аксиом. | 2 |
|
|
| Глава 1. Параллельность прямых и плоскостей | 16 |
|
|
| §1.Параллельность прямых и плоскостей, прямой и плоскости. | 4 |
|
| 4 | Параллельные прямые в пространстве. | 1 |
|
| 5 | Параллельность трех прямых. | 1 |
|
| 6 | Параллельность прямой и плоскости. | 1 |
|
|
| Решение задач по теме « Параллельность прямых и плоскостей». | 1 |
|
|
| §2.Взаимное расположение прямых в пространстве. Угол между двумя прямыми. | 4 |
|
| 7 | Скрещивающиеся прямые. | 1 |
|
| 8 | Углы с сонаправленными сторонами. | 1 |
|
| 9 | Угол между прямыми. | 1 |
|
|
| Решение задач. Контрольная работа №1 по теме « Параллельность прямых и плоскостей, прямой и плоскости. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. (20 мин.) | 1 |
|
|
| §3.Параллельность плоскостей. | 2 |
|
| 10 | Параллельные плоскости. Работа над ошибками. | 1 |
|
| 11 | Свойства параллельных плоскостей. | 1 |
|
|
| §4.Тетраэдр и параллелепипед. | 4 |
|
| 12 | Тетраэдр. | 1 |
|
| 13 | Параллелепипед. | 1 |
|
| 14 | Задачи на построение сечений. | 1 |
|
|
| Решение задач по теме « Тетраэдр и параллелепипед». | 1 |
|
|
| Контрольная работа 2 по теме « Параллельность прямых и плоскостей» | 1 |
|
|
| Зачет № 1 по теме « Параллельность прямых и плоскостей» | 1 |
|
|
| Глава 2. Перпендикулярность прямых и плоскостей. | 17 |
|
|
| §1.Перпендикулярность прямой и плоскости. | 5 |
|
| 15 | Перпендикулярные прямые в пространстве. | 1 |
|
| 16 | Параллельные прямые, перпендикулярные к плоскости. | 1 |
|
| 17 | Признак перпендикулярность прямой и плоскости. | 1 |
|
| 18 | Теорема о прямой, перпендикулярной к плоскости. | 1 |
|
|
| Решение задач по теме « Перпендикулярность прямой и плоскости». | 1 |
|
|
| §2.Перпендикуляр и наклонные. Угол между прямой и плоскостью. | 6 |
|
| 19 | Расстояние от точки до плоскости. | 1 |
|
| 20 | Теорема о трех перпендикулярах. | 1 |
|
| 21 | Угол между прямой и плоскостью. | 1 |
|
|
| Решение задач по теме « Перпендикуляр и наклонные. Угол между прямой и плоскостью». | 3 |
|
|
| §3.Двугранный угол. Перпендикулярность плоскостей | 4 |
|
| 22 | Двугранный угол. | 1 |
|
| 23 | Признак перпендикулярности двух плоскостей. | 1 |
|
| 24 | Прямоугольный параллелепипед. | 1 |
|
| 25,26 | Трехгранный угол. Многогранный угол. | 1 |
|
|
| Контрольная работа 3 по теме « Перпендикулярность прямых и плоскостей». | 1 |
|
|
| Зачет № 2 по теме «Перпендикулярность прямых и плоскостей» | 1 |
|
|
| Глава 3. Многогранники. | 14 |
|
|
| §1.Понятие многогранника. Призма. | 3 |
|
| 27,28 | Понятие многогранника. Геометрическое тело. Работа над ошибками. | 1 |
|
| 29 | Теорема Эйлера. | 1 |
|
| 30,31 | Призма. Пространственная теорема Пифагора. | 1 |
|
|
| §2.Пирамида. | 4 |
|
| 32 | Пирамида. | 1 |
|
| 33 | Правильная пирамида. | 1 |
|
| 34 | Усеченная пирамида. | 1 |
|
|
| Решение задач по теме « Пирамида. Призма». | 1 |
|
|
| §3.Правильные многогранники | 5 |
|
| 35 | Симметрия в пространстве. | 1 |
|
| 36 | Понятие правильного многогранника. | 1 |
|
| 37 | Элементы симметрии правильных многогранников. | 1 |
|
|
| Решение задач по теме «Многогранники». | 2 |
|
|
| Контрольная работа 4 по теме « Многогранники» | 1 |
|
|
| Зачет № 3 по теме « Многогранники» | 1 |
|
|
| Повторение | 3 |
|
|
| Повторение по теме « Параллельность прямых и плоскостей». Работа над ошибками. | 1 |
|
|
| Повторение по теме « Перпендикулярность прямых и плоскостей». | 1 |
|
и 
.
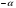х = а. Работа над ошибками.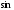
х = а.
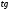х = а.
