ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочие программы основного общего образования по алгебре составлены на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В них также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Сознательное овладение учащимися системой алгебраических знаний и умений необходимо в повседневной жизни для изучения смежных дисциплиной продолжения образования. Практическая значимость школьного курса алгебры обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении алгебре способствует усвоению предметов гуманитарного цикла. Практические умения и навыки алгебраического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении алгебраических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте алгебры в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся и качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, алгебра развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Изучение алгебры, функций, вероятности и статистики существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.
Изучение алгебры позволяет формировать умения и навыки умственного труда — планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов. В процессе изучения алгебры школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса алгебры является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Тем самым алгебра занимает одно из ведущих мест в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание учащихся.
ОБЩАЯ ХАРАКТЕРИСТИКА КУРСА
В курсе алгебры можно выделить следующие основные содержательные линии: арифметика; алгебра; функции; вероятность и статистика. Наряду с этим в содержание включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая линия — «Логика и множества» — служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — способствует созданию общекультурного, гуманитарного фона изучения курса.
Содержание линии «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе, в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе.
Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности. Язык алгебры подчёркивает значение математики как языка для построения математических моделей процессов и явлений реального мира.
Развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений также являются задачами изучения алгебры. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
МЕСТО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Базисный учебный (образовательный) план на изучение алгебры в 7—9 классах основной школы отводит 4 часа в неделю в течение каждого года обучения, всего 416 уроков.
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОБУЧЕНИЯ И ОСВОЕНИЮ СОДЕРЖАНИЯ
КУРСА
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
1) сформированность ответственного отношения к учению,
готовность и способности обучающихся к саморазвитию и
самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных
интересов;
2) сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и
младшими, в образовательной, общественно полезной,
учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и
контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически
некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
умение самостоятельно планировать альтернативные пути
достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу
действия на уровне произвольного внимания и вносить необходимые коррективы;
3) умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований
и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное,
дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знакомо-символические средства, модели и схемы для решения
учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять
цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в
группе: находить общее решение и разрешать конфликты
на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
9) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной
речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных
математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
овладение основными способами представления и анализа статистических данных; умение решать задачи на нахождение частоты и вероятности случайных событий;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
СОДЕРЖАНИЕ КУРСА
АРИФМЕТИКА
Рациональные числа. Расширение множества натуральных чисел до множества целых. Множества целых чисел до множества рациональных. Рациональное число как отношение m/n, где т — целое число, п — натуральное. Степень с целым показателем.
Действительные числа. Квадратный корень из числа. Корень третьей степени. Запись корней с помощью степени с дробным показателем.
Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
Множество действительных чисел; представление действительных чисел бесконечными десятичными дробями. Сравнение действительных чисел.
Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени десяти в записи числа. Приближённое значение величины, точность приближения. Прикидка и оценка результатов вычислений.
АЛГЕБРА
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Степень с натуральным показателем и её свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трёхчлен; разложение квадратного трёхчлена на множители.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и её свойства.
Рациональные выражения и их преобразования. Доказательство тождеств.
Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения. Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений.
Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-рациональных уравнений.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.
Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства. Числовые неравенства и их свойства.
Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
ФУНКЦИИ
Основные понятия. Зависимости между величинами. Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, её график и свойства. Квадратичная функция, её график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства. Графики функций у = 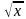 , у =
, у = 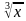 , у = | х |.
, у = | х |.
Числовые последовательности. Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой п-го члена.
Арифметическая и геометрическая прогрессии. Формулы п-го члена арифметической и геометрической прогрессий, суммы первых п-х членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
ВЕРОЯТНОСТЬ И СТАТИСТИКА
Описательная статистика. Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Частота случайного события.
Статистический подход к понятию вероятности. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
ЛОГИКА И МНОЖЕСТВА
Теоретико-множественные понятия. Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств, разность множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера — Венна.
Элементы логики. Понятие о равносильности, следовании, употребление логических связок если..., то ..., в том и только в том случае, логические связки и, или.
МАТЕМАТИКА В ИСТОРИЧЕСКОМ РАЗВИТИИ
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Зарождение алгебры в недрах арифметики. Аль -Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырёх. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.
Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ КУРСА АЛГЕБРЫ В 7-9 КЛАССАХ
РАЦИОНАЛЬНЫЕ ЧИСЛА
Выпускник научится:
понимать особенности десятичной системы счисления;
владеть понятиями, связанными с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применять калькулятор;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Выпускник получит возможность:
познакомиться с позиционными системами счисления с основаниями, отличными от 10;
углубить и развить представления о натуральных числах и свойствах делимости;
научиться использовать приёмы, рационализирующие
вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Выпускник научится:
использовать начальные представления о множестве действительных чисел;
владеть понятием квадратного корня, применять его в вычислениях.
Выпускник получит возможность:
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
ИЗМЕРЕНИЯ, ПРИБЛИЖЕНИЯ, ОЦЕНКИ
Выпускник научится:
1) использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Выпускник научится:
владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
4) выполнять разложение многочленов на множители.
Выпускник получит возможность:
научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
УРАВНЕНИЯ
Выпускник научится:
решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Выпускник получит возможность:
4) овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных
предметов, практики;
5) применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
НЕРАВЕНСТВА
Выпускник научится:
понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
разнообразным приёмам доказательства неравенств; уверенно применять аппарат "неравенств для решения разнообразных математических задач и задач из смежных
предметов, практики;
применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
Выпускник научится:
понимать и использовать функциональные понятия и язык (термины, символические обозначения);
строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Выпускник научится:
понимать и использовать язык последовательностей (термины, символические обозначения);
применять формулы, связанные с арифметической и геометрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе
с контекстом из реальной жизни.
Выпускник получит возможность научиться:
решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;
понимать арифметическую и геометрическую прогрессии как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты, опроса в виде таблицы, диаграммы.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
КОМБИНАТОРИКА
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.
Линия учебно-методических комплектов авторов Г. В. Дорофеева и др.
Дорофеев Г. В. Алгебра, 7 кл.: учебник для общеобразовательных организаций / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др. — М.: Просвещение, 2016.
Дорофеев Г. В. Алгебра, 8 кл.: учебник для общеобразовательных организаций / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др. — М.: Просвещение, 2018.
Дорофеев Г. В. Алгебра, 9 кл.: учебник для общеобразовательных организаций / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др. — М.: Просвещение, 2016.
Минаева С. С. Алгебра, 7 кл.: рабочая тетрадь/ С. С. Минаева, Л. О. Рослова. — М.: Просвещение, 2016.
Минаева С. С. Алгебра, 8 кл.: рабочая тетрадь. В 2 ч. / С. С. Минаева, Л. О. Рослова. — М.: Просвещение, 2017.
Минаева С. С. Алгебра, 9 кл.: рабочая тетрадь. В 2 ч. / С. С. Минаева, Л. О. Рослова. — М.: Просвещение, 2016.
Евстафьева Л. П. Алгебра, 7 кл.: дидактические материалы/Л. П. Евстафьева, А. П. Карп. — М.: Просвещение, 2018.
Евстафьева Л. П. Алгебра, 8 кл.: дидактические материалы/Л. П. Евстафьева, А. П. Карп. — М.: Просвещение, 2017.
Евстафьева Л. П. Алгебра, 9кл.: дидактические материалы/Л. П. Евстафьева, А. П. Карп. — М.: Просвещение, 2017.
.Кузнецова Л. В. Алгебра, 7 кл.: тематические тесты / Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова и др. — М.: Просвещение, 2016.
Кузнецова Л. В. Алгебра, 8 кл.: тематические тесты / Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова и др. — М.: Просвещение, 2016.
Кузнецова Л. В. Алгебра, 9 кл.: тематические тесты / Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова и др. — М.: Просвещение, 2016.
Кузнецова Л. В. Алгебра, 7—9 кл.: контрольные работы/Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова. — М.: Просвещение, 2016.
Суворова С. Б. Алгебра, 7 кл.: методические рекомендации/С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова и др. — М.: Просвещение, 2015.
Суворова С. Б. Алгебра, 8 кл.: методические рекомендации/С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова и др. — М.: Просвещение, 2015.
Суворова С. Б. Алгебра, 9 кл.: методические рекомендации /С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова и др. — М.: Просвещение, 2017.
Календарно-тематическое планирование уроков алгебры в 8-х классах
| Наименование раздела | Дата | Тема урока | Кол-во часов | Элементы содержания | Дом. задание и подробности урока | Предметные результаты | Метапредметные: познавательные, коммуникативные, регулятивные | Личностные результаты |
| Повторение (7 часов) | 1 | «Разложение многочлена на множители» | 1 | Разложение многочлена на множители | Без домашнего задания | Выполняют разложение многочленов на множители, применяя различные способы | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют выполнять различные роли в группе, сотрудничают в совместном решении задач. | Объясняют самому себе свои наиболее заметные достижения; проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную оценку и самооценку учебной деятельности; понимают причины успеха в учебной деятельности |
|
| 2 | «Разложение многочлена на множители» | 1 | Разложение многочлена на множители | дидактика №1(1), 2(1), 3(1, 2) | Анализируют многочлен и распознают возможность применения того или иного приёма разложения его на множители. | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют выполнять различные роли в группе, сотрудничают в совместном решении задач. | Объясняют самому себе свои отдельные ближайшие цели саморазвития; проявляют положительное отношение к урокам математики; понимают причины успеха в учебной деятельности; дают адекватную оценку и самооценку учебной деятельности; анализируют соответсвие результатов требованиям конкретной учебной задачи |
|
| 3 | «Формулы сокращенного умножения» | 1 | Формулы сокращенного умножения | Карточка для инд. работы № 3 | Выполняют разложение многочленов на множители, применяя формулы сокращенного умножения. | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют принимать точку зрения другого | Проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную самооценку учебной деятельности; понимают причины успеха в учебной деятельности; анализируют соответствие результатов требованиям учебной задачи |
|
| 4 | «Формулы сокращенного умножения» | 1 | Формулы сокращенного умножения | Карточка для инд. работы № 4 | Выполняют разложение многочленов на множители, применяя формулы сокращенного умножения. | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют принимать точку зрения другого | Выражают положительное отношение к процессу познания; адекватно оценивают свою учебную деятельность; применяют правила делового сотрудничества |
|
| 5 | «Решение уравнений с помощью разложения на множители» | 1 | Разложение многочлена на множители; уравнения | Карточка для инд. работы № 5 | Решают уравнения разного уровня сложности с помощью разложения на множители. | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют принимать точку зрения другого | Проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную самооценку учебной деятельности; |
|
| 6 | «Разложение многочлена на множители» | 1 | Разложение многочлена на множители | Карточка для инд. работы № 6 | Выполняют разложение многочленов на множители, применяя различные способы | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют выполнять различные роли в группе, сотрудничают в совместном решении задач. | Объясняют самому себе свои наиболее заметные достижения; проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную оценку и самооценку учебной деятельности; понимают причины успеха в учебной деятельности |
|
| 7 | Входная контрольная работа. | 1 |
| Без домашнего задания | Контроль знаний учащихся курса алгебры 7 класса | Выполняют контрольную работу | Выражают положительное отношение к процессу познания; адекватно оценивают свою учебную деятельность; применяют правила делового сотрудничества |
| Глава 1. Алгебраические дроби (27 часов) | 8 | Что такое алгебраическая дробь? | 1 | Алгебраическая дробь. Множество допустимых значений. | дидактика №4, 5(1), 7(1) | Конструируют алгебраические выражения. Находят область определения дроби; выполняют числовые подстановки и вычисляют значение дроби, в том числе с помощью калькулятора | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом и развернутом виде. Коммуникативные - умеют оформлять мысли в устной и письменной речи с учетом ситуаций. | Объясняют самому себе свои наиболее заметные достижения; проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную оценку и самооценку учебной деятельности; понимают причины успеха в учебной деятельности |
|
| 9 | Основное свойство дроби | 1 | Основное свойство алгебраической дроби. Сокращение дробей. Приведение дробей к общему знаменателю. | п.1.1, №4 (б,г), №7(б,г,е,з), № 13(б,г,е) | Формулируют основное свойство алгебраической дроби и применяют его для преобразования дробей | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют слушать других, пытаются принимать другую точку зрения, готовы изменить свою точку зрения. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и сверстников; анализируют соответствие результатов требованиям конкретной учебной задачи |
|
| 10 | Сокращение дробей | 1 | Разложение на множители числителя и знаменателя дробей и сокращение дробей
| п.1.2, №20 (б), 21(б,г), 22(б,г | Формулируют основное свойство алгебраической дроби и применяют его для преобразования дробей | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - преобразовывают модели с целью выявления общих законов, определяющих предметную область. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее. | Проявляют познавательный интерес к изучению предмета, оценивают свою учебную деятельность, применяют правила делового сотрудничества |
|
| 11 | Основное свойство дроби. Самостоятельная работа №1 по теме: «Сокращение дробей» | 1 | Сокращение дробей. | )№26, 27 (в,г) | Формулируют основное свойство алгебраической дроби и применяют его для преобразования дробей | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют слушать других, принимать другую точку зрения, готовы изменить свою точку зрения. | Объясняют самому себе свои наиболее заметные достижения; проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; адекватно воспринимают оценку учителя |
|
| 12-13 | Сложение и вычитание алгебраических дробей | 2 | Правила сложения и вычитания алгебраических дробей.. | п.1.2, №36, 37 (г,д,е) | Выполняют сложение, вычитание алгебраических дробей. Применяют преобразование выражений | Регулятивные - составляют план выполнения задач, решают проблемы творческого и поискового характера. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее. | Проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную самооценку учебной деятельности; понимают причины успеха в учебной деятельности; анализируют соответствие результатов требованиям учебной задачи |
|
| 14-15 | Решение задач по теме: «Сложение и вычитание алгебраических дробей» | 2 | Правила сложения и вычитания алгебраических дробей. | п.1.3 №46 (г,д,е), 50 (б,г,е) | Выполняют сложение, вычитание алгебраических дробей. Применяют преобразование выражений | Регулятивные - составляют план выполнения задач, решают проблемы творческого и поискового характера. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций. | Объясняют самому себе свои отдельные ближайшие цели саморазвития; проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач; доброжелательное отношение к сверстникам; адекватно воспринимают оценку учителя |
|
| 16 | Упрощение выражений. Самостоятельная работа № 2 по теме: «Сложение и вычитание алгебраических дробей» | 1 | Правила сложения и вычитания алгебраических дробей. | №55 (г,д,е), 57 (г,д,е), 65(в,г) | Выполняют сложение, вычитание алгебраических дробей. Применяют преобразование выражений | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - записывают выводы в виде правил "если…, то…". Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; адекватно воспринимают оценку учителя |
|
| 17-18 | Умножение и деление алгебраических дробей | 2 | Правила умножения и деления алгебраических дробей. | № 63, 68(в,г)
| Выполняют умножение и деление алгебраических дробей. Применяют преобразование выражений | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют выполнять различные роли в группе, сотрудничают в совместном решении задачи. | Проявляют познавательный интерес к изучению предмета, способам решения учебных задач; дают адекватную самооценку учебной деятельности; понимают причины успеха/неуспеха в учебной деятельности; анализируют соответствие результатов требованиям учебной задачи |
|
| 19 | Упрощение выражений. Самостоятельная работа №3 по теме: «Умножение и деление алгебраических дробей» | 1 | Правила умножения и деления алгебраических дробей. | п.1.4, №73 (б), 74 (б) 79(д,е,ж,з) | Выполняют умножение и деление алгебраических дробей. Применяют преобразование выражений | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Выражают положительное отношение к процессу познания; адекватно оценивают свою учебную деятельность; применяют правила делового сотрудничества |
|
| 20-22 | Преобразование выражений, содержащих алгебраические дроби | 3 | Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. | №86 (б), 88 (б) | Выполняют действия алгебраических дробей. Применяют преобразование выражений для решения задач. | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменить свою точку зрения. | Проявляют познавательный интерес к изучению предмета, оценивают свою учебную деятельность, применяют правила делового сотрудничества |
|
| 23 | Преобразование выражений, содержащих алгебраические дроби | 1 | Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. | п.1.5, №91 (б,г,е), 94(в,г) | Выражают переменные из формул (физических, геометрических, описывающих бытовые ситуации). | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников (справочники, Интернет). Коммуникативные - умеют понимать точку зрения другого, слушать друг друга. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают оценку результатов своей учебной деятельности |
|
| 24 | Упрощение выражений. Самостоятельная работа №4 по теме: «Преобразование алгебраических выражений» | 1 | Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. | №95(б), 97(б), 102(а) | Проводят исследования, выявляют закономерности | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - записывают выводы в виде правил "если…, то…". Коммуникативные - умеют оформлять мысли в устной и письменной речи с учетом речевых ситуаций. | Принимают и осваивают роль обучающегося; проявляют познавательный интерес к изучению предмета; дают адекватную оценку своей учебной деятельности |
|
| 25 | Определение степени с целым показателем | 1 | Степень с целым показателем и ее свойства. Выделение множителя — степени десяти — в записи числа. 5Стандартный вид числа.
| №99 | Формулируют определение степени с целым показателем | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом речевых ситуаций. | Объясняют отличия в оценках одной и той же ситуации разными людьми, принимают роль ученика, проявляют познавательный интерес к изучению предмета |
|
| 26 | Степень с целым показателем | 1 | Степень с целым показателем и ее свойства. Выделение множителя — степени десяти — в записи числа. Стандартный вид числа.
| п.1.6, № 107(в,г), 108 (б,г,е) | Формулируют определение степени с целым показателем | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 27 | Свойства степеней с целым показателем | 1 | Свойства степени с целым показателем. Миллиардная часть метра – нанометр. | № 114, 125 (б,г,е) 126 (б,г,е) | Формулируют, записывают в символической форме и иллюстрируют примерами свойства степени с целым показателем; применяют свойства степени для преобразования выражений и вычислений. | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения |
|
| 28 | Свойства степеней с целым показателем. Самостоятельная работа №5 по теме: «Свойства степеней с целым показателем» | 1 | Степень с целым показателем и ее свойства. | п.1.7, №148(б,г,е) №149(б,г,е) №150(б,г,е,з) | Используют запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивают числа и величины, записанные с использованием степени 10. Выполняют вычисления с реальными данными. Выполняют прикидку и оценку результатов вычислений | Регулятивные - работают по составленному плану, используют основные и дополнительные средства (справочная литература, средства ИКТ). Познавательные - сопоставляют и отбирают информацию, полученную из разных источников (справочники, Интернет). Коммуникативные - умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций. | Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету |
|
| 29-30 | Решение уравнений | 2 | Решение линейных уравнений, коэффициентами которых являются обыкновенные или десятичные дроби. Уравнения, составленные из алгебраических дробей. | №152,155 | Решают уравнения с дробными коэффициентами, | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют принимать точку зрения другого | Проявляют устойчивый интерес к способам решения познавательных задач, положительное отношение к урокам математики |
|
| 31-32 | Решение задач | 2 | Решение задач с использованием линейных уравнений.
| п.1.8, №167 168(б,г) | Решают текстовые задачи алгебраическим методом | Регулятивные - пределяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют интерес к изучению предмета, дают положительную оценку и самооценку результатам деятельности |
|
| 33 | Подготовка к контрольной работе по теме: «Алгебраические дроби» | 1 | Решение линейных уравнений. Решение задач с использованием линейных уравнений. | № 170,173 | Конструируют алгебраические выражения. Находят область определения алгебраической дроби; выполняют числовые подстановки и вычисляют значение дроби, в том числе с помощью калькулятора. Выполняют действия алгебраических дробей. Применяют преобразование выражений для решения задач. Выражают переменные из формул (физических, геометрических, описывающих бытовые ситуации). Проводят исследования, выявляют закономерности. Формулируют, записывают в символической форме и иллюстрируют примерами свойства степени с целым показателем; применяют свойства степени для преобразования выражений и вычислений. Используют запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивают числа и величины, записанные с использованием степени 10. | Регулятивные - Определяют цель учебной деятельности, осуществляют поиск средств ее осуществления. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач, дают позитивную оценку и самооценку учебной деятельности |
|
| 34 | Контрольная работа №1 по теме: «Алгебраические дроби» | 1 | Сложение и вычитание, умножение и деление алгебраических дробей. Преобразование выражений, содержащих алгебраические дроби. Свойства степени с целым показателем. | №176,178 | Конструируют алгебраические выражения. Находят область определения алгебраической дроби; выполняют числовые подстановки и вычисляют значение дроби, в том числе с помощью калькулятора. Выполняют действия алгебраических дробей. Применяют преобразование выражений для решения задач. Выражают переменные из формул (физических, геометрических, описывающих бытовые ситуации). Проводят исследования, выявляют закономерности. Формулируют, записывают в символической форме и иллюстрируют примерами свойства степени с целым показателем; | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - делают предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - умеют слушать других, принимать точку зрения другого, изменить свою точку зрения. | Принимают и осваивают социальную роль обучающегося; проявляют мотивы своей учебной деятельности; понимают личностный смысл учения |
| Глава 2. Квадратные корни (22 часа) | 35 | Анализ результатов КР. Работа над ошибками. Задача о нахождении стороны квадрата | 1 | Квадратный корень. Площадь квадрата. Символ √ | Без домашнего задания | Формулируют определения квадратного корня из числа, решают задачи, приведшие к понятию квадратного корня | Регулятивные - работают по составленному плану, используют основные и дополнительные средства информации. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее, подтверждая аргументы фактами. | Объясняют самому себе свои наиболее заметные достижения; проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач; доброжелательное отношение к сверстникам; дают адекватную оценку учебной деятельности |
|
| 36-37 | Вычисление квадратных корней | 2 | Квадратный корень. Площадь квадрата. Символ √ | п.2.1, №225(б,г,е,з), 226(б,г,е), 225 | Вычисляют квадратные корни | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - записывают выводы в виде правил "если..., то...". Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Объясняют самому себе свои наиболее заметные достижения; проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач; доброжелательное отношение к сверстникам; дают адекватную оценку учебной деятельности |
|
| 38 | Иррациональные числа | 1 | Иррациональные числа. Действительные числа. | №236,241 | Приводят примеры иррациональных чисел; распознают иррациональные и рациональные числа. Описывают множество действительных чисел. Изображают числа точками координатной прямой | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом речевых ситуаций. | Объясняют отличия в оценках одной и той же ситуации разными людьми, проявляют познавательный интерес к изучению предмета, дают адекватную оценку своей учебной деятельности |
|
| 39 | Теорема Пифагора. Самостоятельная работа №6 по теме: «Квадратные корни» | 1 | Теорема Пифагора. Решение задач с применением теоремы Пифагора. | п.2.2№250,252, 258 | Формулируют теорему Пифагора, умеют находить любую сторону прямоугольного треугольника, если известны две другие | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средства ее достижения. Познавательные - делают предположения об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее, подтверждать аргументы фактами. | Понимают необходимость учения, осваивают и принимают социальную роль обучающегося, дают адекватную оценку результатам своей учебной деятельности |
|
| 40 | Квадратный корень (алгебраический подход) | 1 | Определение квадратного корня.. Арифметический квадратный корень. Число решений уравнения х2= а. | п.2.3, №275,277, 260 | Применяют график функции у = х2 для нахождения корней квадратных уравнений, используют при необходимости калькулятор; проводят оценку квадратных корней | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи.Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 41-42 | График зависимости у = | 2 | Графики зависимостей y= | п.2.4, №294(б,г,е) 298(б,г,е), 302 | Строят график функции у = | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения |
|
| 43-44 | Свойства квадратных корней | 2 | Теоремы о корне из произведения и частного.
| п.2.5 №310(б,г,е) 314, 315 | Доказывают свойства арифметических квадратных корней; применяют их к преобразованию выражений | Регулятивные - работают по составленному плану, используют основные и дополнительные средства получения информации. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее, подтверждать аргументы фактами. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 45-46 | Использование свойств квадратного корня при упрощении | 2 | Теоремы о корне из произведения и частного.
| п.2.6, №320-323(б,г,е) | Доказывают свойства арифметических квадратных корней; применяют их к преобразованию выражений | Регулятивные - работают по составленному плану, используют основные и дополнительные средства для получения информации (справочная литература, средства ИКТ). Познавательные - записываю выводы в виде правил «если …, то …». Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее. | Дают положительную адекватную самооценку на основе заданных критериев успешности учебной деятельности, проявляют познавательный интерес к предмету |
|
| 47-48 | Свойства квадратного корня | 2 | Теоремы о корне из произведения и частного.
| №332,337, 340 | Доказывают свойства арифметических квадратных корней; применяют их к преобразованию выражений | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - делают предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - понимают точку зрения другого. | Проявляют положительное отношение к урокам математики, широкий интерес к способам решения новых учебных задач, понимают причины успеха в своей учебной деятельности |
|
| 49-51 | Преобразование выражений, содержащих квадратные корни | 3 | Подобные радикалы. Равенство. Освобождение от иррациональности в знаменателе дроби. | №343,348 | Преобразовывают выражения, содержащие квадратные корни | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее, подтверждать аргументы фактами. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают социальную роль ученика |
|
| 52-53 | Преобразование выражений, содержащих квадратные корни. Самостоятельная работа №7 по теме: «Преобразование выражений» | 2 | Подобные радикалы. Равенство. Освобождение от иррациональности в знаменателе дроби. | п.2.7, №354 (б,г,е,ж,и), 356 (б,г,е), 359 (б,г) | Преобразовывают выражения, содержащие квадратные корни | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - записывают выводы правил "если…, то…". Коммуникативные - организовывают учебное взаимодействие в группе. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют положительное отношение к урокам математики, дают самооценку результатов своей учебной деятельности |
|
| 54 | Кубический корень | 1 | Определение кубического корня. Зависимость y= | №363,368 | Формулируют определение кубического корня из числа, вычисляют кубические корни из числа | Регулятивные - работают по составленному плану, используют основные и дополнительные средства для получения информации. Познавательные - передают содержание в сжатом, выборочном и развернутом виде. Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее, подтверждая фактами. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 55 | Подготовка к контрольной работе: «Квадратные корни» | 1 | Квадратные корни, корни n-ой степени, графики зависимостей: y= | п.2.8, №393, 394 | Формулируют определения квадратного корня из числа, решают задачи, приведшие к понятию квадратного корня. Приводят примеры иррациональных чисел; распознают иррациональные и рациональные числа. Описывают множество действительных чисел. Изображают числа точками координатной прямой. Формулируют теорему Пифагора, умеют находить любую сторону прямоугольного треугольника, если известны две другие. Строят график функции у = | Регулятивные - В диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Куют оммуникативные - умеют критично относиться к своему мнению. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач, дают позитивную оценку и самооценку учебной деятельности, адекватно воспринимают оценку учителя и сверстников, анализируют соответствие результатов требованиям учебной задачи |
|
| 56 | Контрольная работа №2 по теме: «Квадратные корни» | 1 | Квадратные корни, корни n-ой степени, графики зависимостей: y= | стр 118 (1-18) | Формулируют определения квадратного корня из числа, решают задачи, приведшие к понятию квадратного корня. Приводят примеры иррациональных чисел; распознают иррациональные и рациональные числа. Описывают множество действительных чисел. Изображают числа точками координатной прямой. Формулируют теорему Пифагора, умеют находить любую сторону прямоугольного треугольника, если известны две другие. Строят график функции у = | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют выполнять различные роли в группе, сотрудничать в совместном решении учебной задачи. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач. доброжелательное отношение к сверстникам, адекватно воспринимают оценку учителя, понимают причины успеха в учебной деятельности |
| Глава 3. Квадратные уравнения (24 часа) | 57 | Анализ результатов КР. Работа над ошибками. Какие уравнения называются квадратными | 1 | Квадратное уравнение. Коэффициенты. Приведенное квадратное уравнение
| Без домашнего задания | Распознают квадратные уравнения, классифицируют их | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 58 | Формула корней квадратного уравнения | 1 | Формула корней квадратного уравнения. Дискриминант. Знак дискриминанта и число корней.
| п.3.1, №424(в), 428(б,г), 430 | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения |
|
| 59-60 | Решение квадратных уравнений | 2 | Формула корней квадратного уравнения. Дискриминант. Знак дискриминанта и число корней.
| п.3.2, №435(б,г,е) 436(б,г,е,з) | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - составляют план выполнения задач, решают проблемы творческого и поискового характера. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают адекватную оценку результатов своей учебной деятельности |
|
| 61 | Решение квадратных уравнений | 1 | Формула корней квадратного уравнения. Дискриминант. Знак дискриминанта и число корней.
| №438(б,г,е,з), 439(б.г), 440(б,г,е) | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средства ее достижения. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют выполнять различные роли в группе, сотрудничать в совместном решении задачи. | Объясняют отличия в оценках одной и той же ситуации разными людьми, проявляют положительное отношение к урокам математики, дают положительную оценку и самооценку результатов учебной деятельности |
|
| 62 | Решение квадратных уравнений. Самостоятельная работа №8 по теме: «Квадратные уравнения» | 1 | Формула корней квадратного уравнения. Дискриминант. Знак дискриминанта и число корней.
| №441(б,г,е) 442(б,г,е,з) | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - строят предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - умеют отстаивать свою точку зрения, аргументируя ее, подтверждать аргументы фактами. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают социальную роль ученика |
|
| 63-64 | Вторая формула корней квадратного уравнения | 2 | Квадратные уравнения с четным вторым коэффициентом. Уравнения высших степеней. | №443(б), 446 | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - работают по составленному плану, используют основные и дополнительные средства для получения информации. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Принимают и осваивают социальную роль обучающегося, проявляют мотивы своей учебной деятельности, дают адекватную оценку своей учебной деятельности |
|
| 65 | Решение квадратных уравнений с помощью второй формулы | 1 | Квадратные уравнения с четным вторым коэффициентом. Уравнения высших степеней. | п.3.3, №449(б,г,е,з),450(б) | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают полные квадратные уравнения. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - записывают выводы в виде правил "если…, то…". Коммуникативные - умеют организовать учебное взаимодействие в группе (распределяют роли, договариваются друг с другом и т. д.) | Объясняют самому себе свои наиболее заметные достижения, понимают причины успеха в своей учебной деятельности, дают адекватную оценку результатам учебной деятельности, проявляют интерес к предмету |
|
| 66-67 | Решение задач | 2 | Текстовые задачи с арифметическим, геометрическим, физическим содержанием, с экономическими фабулами. Математическая модель. Применение при решении задач квадратных уравнений. | №451(б,г,е,з),454 | Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решают составленное уравнение; интерпретируют результат | Регулятивные - работают по составленному плану, используют основные и дополнительные средства (справочная литература, средства ИКТ). Познавательные - сопоставляют и отбирают информацию, полученную из разных источников (справочники, Интернет). Коммуникативные - умеют выполнять различные роли в группе, сотрудничать в совместном решении задачи. | Объясняют отличия в оценках одной и той же ситуации разными людьми, принимают социальную роль ученика, проявляют познавательный интерес к изучению предмета, дают адекватную оценку своей учебной деятельности |
|
| 68 | Решение задач | 1 | Текстовые задачи с арифметическим, геометрическим, физическим содержанием, с экономическими фабулами. Математическая модель. Применение при решении задач квадратных уравнений. | п.3.4,№ 465-467(б) | Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решают составленное уравнение; интерпретируют результат | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Проявляют положительное отношение к урокам математики, широкий интерес к способам решения новых учебных задач, понимают причины успеха в своей учебной деятельности |
|
| 69-70 | Неполные квадратные уравнения | 2 | Неполные квадратные уравнения. Приемы решения уравнений | №469,471, 474 | Решают неполные квадратные уравнения | Регулятивные - определяют цель учебной деятельности, осуществляют средства ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют понимать точку зрения другого. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, к способам решения учебной задачи |
|
| 71 | Неполные квадратные уравнения. Самостоятельная работа №9 по теме: «Неполные квадратные уравнения» | 1 | Неполные квадратные уравнения. Приемы решения уравнений | п.3.5, №490-493(б,г,е) | Решают неполные квадратные уравнения | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - преобразовывают модели с целью выявления общих законов, определяющих предметную область. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Проявляют положительное отношение к урокам математики, осваивают и принимают социальную роль обучающегося, понимают причины успеха своей учебной деятельности |
|
| 72 | Теорема Виета | 1 | Теорема Виета. Формулы Виета. Теорема, обратная теореме Виета. | №495(б,г,е,з),499(б) | Проводят простейшие исследования квадратных уравнений. Наблюдают и анализируют связь между корнями и коэффициентами квадратного уравнения. Формулируют и доказывают теорему Виета, а также обратную теорему, применют эти теоремы для решения разнообразных задач | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Дают позитивную самооценку результатам деятельности, понимают причины успеха в своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 73-74 | Решение квадратных уравнений с помощью теоремы Виета | 2 | Теорема Виета. Формулы Виета. Теорема, обратная теореме Виета. | п.3.6,№516(б,г),519 | Используют различные приемы проверки правильности выполняемых заданий | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 75 | Разложение квадратного трехчлена на множители | 1 | Определение квадратного трехчлена. Дискриминант квадратного трехчлена. Корни квадратного трехчлена. Разложение квадратного трёхчлена на множители. | Без домашнего задания | Распознают квадратный трёхчлен, выясняют возможность разложения на множители, представляют квадратный трёхчлен в виде произведения линейных множителей. Применяют различные приёмы самоконтроля при выполнении преобразований. Проводят исследования квадратных уравнений с буквенными коэффициентами, выявляют закономерности | Регулятивные - работают по составленному плану, используют основные и дополнительные средства. Познавательные - передают содержание в сжатом и развернутом виде. Коммуникативные - умеют организовывать учебное взаимодействие в группе (распределяют роли, договариваются друг с другом и т. д.). | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают адекватную оценку результатов своей учебной деятельности, понимают причины успеха в деятельности |
|
| 76-77 | Сокращение дробей с использованием разложения на множители | 2 | Определение квадратного трехчлена. Дискриминант квадратного трехчлена. Корни квадратного трехчлена. Разложение квадратного трёхчлена на множители. | п.3.7, №534,537 | Распознают квадратный трёхчлен, выясняют возможность разложения на множители, представляют квадратный трёхчлен в виде произведения линейных множителей. Применяют различные приёмы самоконтроля при выполнении преобразований. Проводят исследования квадратных уравнений с буквенными коэффициентами, выявляют закономерности | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Проявляют положительное отношение к урокам математики, широкий интерес к способам решения новых учебных задач, понимают причины успеха в учебной деятельности |
|
| 78 | Разложение на множители. Самостоятельная работа №10 по теме: «Разложение на множители» | 1 | Определение квадратного трехчлена. Дискриминант квадратного трехчлена. Корни квадратного трехчлена. Разложение квадратного трёхчлена на множители. | №538(б,г,е)544(б,г,е) | Распознают квадратный трёхчлен, выясняют возможность разложения на множители, представляют квадратный трёхчлен в виде произведения линейных множителей. Применяют различные приёмы самоконтроля при выполнении преобразований. Проводят исследования квадратных уравнений с буквенными коэффициентами, выявляют закономерности | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположения об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют оформлять мысли в устной и письменной речи с учетом речевых ситуаций. | Объясняют отличия в оценках одной и той же ситуации разными людьми, проявляют положительное отношение к урокам математики |
|
| 79 | Подготовка к контрольной работе по теме: «Квадратные уравнения» | 1 | Квадратные уравнения. Теорема Виета. Задачи. | №540,541 | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают квадратные уравнения – полные и неполные. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной. Наблюдают и анализируют связь между корнями и коэффициентами квадратного уравнения. Формулируют и доказывают теорему Виета, а также обратную теорему, применяют эти теоремы для решения разнообразных задач. Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решают составленное уравнение; интерпретируют результат. Распознают квадратный трёхчлен, выясняют возможность разложения на множители, представляют квадратный трёхчлен в виде произведения линейных множителей. Применяют различные приёмы самоконтроля при выполнении преобразований. Проводят исследования квадратных уравнений с буквенными коэффициентами, выявляют закономерности | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средства ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют понимать точку зрения другого. | Дают позитивную самооценку результатам учебной деятельности, понимают причины успеха в учебной деятельности, проявляют познавательный интерес к предмету |
|
| 80 | Контрольная работа №3 по теме: «Квадратные уравнения» | 1 | Квадратные уравнения. Теорема Виета. Задачи. | стр.167 (1-8) | Распознают квадратные уравнения, классифицируют их. Выводят формулу корней квадратного уравнения. Решают квадратные уравнения – полные и неполные. Проводят простейшие исследования квадратных уравнений. Решают уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной. Наблюдают и анализируют связь между корнями и коэффициентами квадратного уравнения. Формулируют и доказывают теорему Виета, а также обратную теорему, применяют эти теоремы для решения разнообразных задач. Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решают составленное уравнение; интерпретируют результат. Распознают квадратный трёхчлен, выясняют возможность разложения на множители, представляют квадратный трёхчлен в виде произведения линейных множителей. Применяют различные приёмы самоконтроля при выполнении преобразований. Проводят исследования квадратных уравнений с буквенными коэффициентами, выявляют закономерности | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют понимать точку зрения другого, слушают. | Объясняют самому себе свои наиболее заметные достижения, проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, понимают причины успеха в учебной деятельности |
| Глава 4. Системы уравнений (24 часа) | 81 | Работа над ошибками. Линейное уравнение с двумя переменными | 1 | Определение линейного уравнения с двумя переменными. Решение уравнений с двумя переменными. Что называется решением уравнения с двумя переменными. | Без домашнего задания | Определяют, является ли пара чисел решением уравнения с двумя переменными; приводят примеры решений уравнений с двумя переменными. Решабт задачи, алгебраической моделью которых является уравнение с двумя переменными; находят целые решения путём перебора. Распознают линейные уравнения с двумя переменными | Регулятивные - составляют план выполнения задач, решения проблем творческого и поискового характера. Познавательные - делают предположения об информации, которая нужна для решения предметной задачи. Коммуникативные - умеют взглянуть на ситуацию с иной позиции и договориться с людьми иных позиций. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают социальную роль ученика |
|
| 82 | График линейного уравнения с двумя переменными | 1 | График уравнения вида: ax + by = c.
| п.4.1№ 576(б,г), 577 (б,г), 581 | Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений | Регулятивные - работают по составленному плану, используют основные и дополнительные средства получения информации. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников.Коммуникативные - умеют выполнять различные роли в группе, сотрудничать в совместном решении задачи. | Объясняют самому себе свои наиболее заметные достижения, адекватно оценивают результаты своей учебной деятельности, проявляют интерес к предмету |
|
| 83 | График линейного уравнения с двумя переменными | 1 | График уравнения вида: ax + by = c.
| п.4.2, № 588(б,г), 589(б,г), 590(б,г,е) | Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, дают положительную оценку результатам своей учебной деятельности, проявляют интерес к предмету |
|
| 84 | Уравнение прямой вида у = kx + l | 1 | Графики зависимостей: y=kx и y=kx+l. Взаимное расположение прямых линейного уравнения в зависимости от коэффициентов. | № 595,596, 597 | Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений; извлекают из уравнения вида у = kx + b информацию о положении прямой в координатной плоскости. Распознают параллельные и пересекающиеся прямые по их уравнениям; конструируют уравнения прямых, параллельных данной прямой. Используют приёмы самоконтроля при построении графиков линейных уравнений | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют принимать точку зрения другого. | Проявляют устойчивый интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают адекватную оценку результатов своей учебной деятельности |
|
| 85 | Уравнение прямой вида у = kx + l | 1 | Графики зависимостей: y=kx и y=kx+l. Взаимное расположение прямых линейного уравнения в зависимости от коэффициентов. | п.4.3, № 609(б,г,е), 610(б,г) | Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений; извлекают из уравнения вида у = kx + b информацию о положении прямой в координатной плоскости. Распознают параллельные и пересекающиеся прямые по их уравнениям; конструируют уравнения прямых, параллельных данной прямой. Используют приёмы самоконтроля при построении графиков линейных уравнений | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - оформляют свои мысли в устной и письменной речи с учетом речевых ситуаций. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 86 | Уравнение прямой вида у = kx + l. Самостоятельная работа №11 по теме: «Уравнение прямой вида у = kx + l» | 1 | Графики зависимостей: y=kx и y=kx+l. Взаимное расположение прямых линейного уравнения в зависимости от коэффициентов. | №618(б,г,е)619(б,г,е) 620(б,г) | Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений; извлекают из уравнения вида у = kx + b информацию о положении прямой в координатной плоскости. Распознают параллельные и пересекающиеся прямые по их уравнениям; конструируют уравнения прямых, параллельных данной прямой. Используют приёмы самоконтроля при построении графиков линейных уравнений | Регулятивные - работают по совместному плану, используют основные и дополнительные средства получения информации. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют высказывать точку зрения, пытаясь ее обосновать, приводя аргументы. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют познавательный интерес к предмету, дают адекватную оценку результатов своей учебной деятельности, понимают причины успеха в учебной деятельности |
|
| 87-88 | Системы уравнений. Решение систем способом сложения | 2 | Условия параллельности прямых. Система уравнений. Решение систем уравнений с двумя переменными способом сложения.
| №621(б,г) 626(б,г) | Решают системы двух линейных уравнений с двумя переменными способом сложения | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 89 | Решение систем способом сложения | 1 | Условия параллельности прямых. Система уравнений. Решение систем уравнений с двумя переменными способом сложения.
| п.4.4, №634 635(б), 636(б,ге) | Решают системы двух линейных уравнений с двумя переменными способом сложения | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - делают предположения об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют уважительно относиться к позиции другого, договариваться. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к предмету |
|
| 90 | Решение систем уравнений способом сложения. Самостоятельная работа №12 по теме: «Системы уравнений» | 1 | Условия параллельности прямых. Система уравнений. Решение систем уравнений с двумя переменными способом сложения.
| №637 (б), 639(б,г,е) 640(б,г,е) | Решают системы двух линейных уравнений с двумя переменными способом сложения | Регулятивные - определяют цель учебной деятельности, ищут средства ее осуществления. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют высказывать свою точку зрения и ее обосновать, приводя аргументы. | Объясняют самому себе свои наиболее заметные достижения, выражают положительное отношение к процессу познания, оценивают свою учебную деятельность |
|
| 91-92 | Решение систем уравнений способом подстановки | 2 | Способ записи систем с помощью фигурной скобки. Решение систем способом сложения и способом подстановки. | №642(б,г,е)645(б,г) | Решают системы двух линейных уравнений с двумя переменными способом подстановки, решают простейшие системы, в которых одно из уравнений не является линейным | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Принимают и осваивают социальную роль обучающегося; проявляют мотивы своей учебной деятельности; понимают личностный смысл учения |
|
| 93 | Решение систем уравнений способом подстановки | 1 | Способ записи систем с помощью фигурной скобки. Решение систем способом сложения и способом подстановки. | п.4.5, №650-651(б,г,е) | Решают системы двух линейных уравнений с двумя переменными способом подстановки, решают простейшие системы, в которых одно из уравнений не является линейным | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - самостоятельно предполагают, какая информация нужна для решения учебной задачи. Коммуникативные - умеют слушать других, принимать другую точку зрения. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач |
|
| 94 | Решение систем уравнений способом подстановки. Самостоятельная работа №13 по теме: «Системы уравнений» | 1 | Способ записи систем с помощью фигурной скобки. Решение систем способом сложения и способом подстановки. | №652(б,г,е) 654(б,г) | Решают системы двух линейных уравнений с двумя переменными способом подстановки, решают простейшие системы, в которых одно из уравнений не является линейным | Регулятивные - составляют план выполнения задач, решения проблем творческого и поискового характера. Познавательные - преобразовывают модели с целью выявления общих законов, определяющих предметную область. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее, подтверждая аргументы фактами. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 95-96 | Решение задач с помощью систем уравнений | 2 | Математическая модель задачи. Система уравнений. Решение уравнения или системы уравнения. Соответствие полученного результата условию задачи | №655(б,г,е) 657(б,г) | Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решают составленную систему уравнений; интерпретируют результат | Регулятивные - работают по составленному плану, используют основные и дополнительные средства. Познавательные - умеют передавать содержание в сжатом, выборочном или развернутом виде. Коммуникативные - при необходимости отстаивают свою точку зрения, аргументируя ее, подтверждают аргументы фактами. | Объясняют самому себе свои отдельные ближайшие цели саморазвития; проявляют познавательный интерес к изучению математики; понимают причины успеха в учебной деятельности; дают адекватную оценку и самооценку учебной деятельности |
|
| 97 | Решение задач на движение | 1 | Математическая модель задачи. Система уравнений. Решение уравнения или системы уравнения. Соответствие полученного результата условию задачи | п.4.6, №664(в) 665(б) 667(б)
| Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решают составленную систему уравнений; интерпретируют результат | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - самостоятельно предполагают, какая информация нужна для решения предметной учебной задачи. Коммуникативные - умеют понимать точку зрения другого. | Объясняют свои наиболее заметные достижения; проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников |
|
| 98-99 | Решение задач на проценты | 2 | Математическая модель задачи. Система уравнений. Решение уравнения или системы уравнения. Соответствие полученного результата условию задачи | №666(б) 675,680(б) | Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решают составленную систему уравнений; интерпретируют результат | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и сверстников; анализируют соответствие результатов требованиям учебной задачи |
|
| 100-101 | Задачи на координатной плоскости | 2 | Применение алгебраического аппарата к решению задач с геометрической тематикой. Координаты точки пересечения прямых. | №669(б) 671(б) 670(б) | Решают системы двух линейных уравнений с двумя переменными графическим способом; используют графические представления для исследования систем линейных уравнений. Применяют алгебраический аппарат для решения задач на координатной плоскости | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 102 | Задачи на координатной плоскости | 1 | Применение алгебраического аппарата к решению задач с геометрической тематикой. Координаты точки пересечения прямых. | п.4.7 №685(б), 687(б) 672(б)
| Решают системы двух линейных уравнений с двумя переменными графическим способом; используют графические представления для исследования систем линейных уравнений. Применяют алгебраический аппарат для решения задач на координатной плоскости | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи.Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения |
|
| 103 | Подготовка к контрольной работе по теме: «Системы уравнений» | 1 | Линейное уравнение с двумя переменными. Графики уравнений вида: ax+by=c иax=by. Системы уравнений с двумя переменными. Задачи. | №686(б), 688(б),689 690 | Определяют, является ли пара чисел решением уравнения с двумя переменными; приводят примеры решений уравнений с двумя переменными. Решают задачи, алгебраической моделью которых является уравнение с двумя переменными; находят целые решения путём перебора. Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений; извлекают из уравнения вида у = kx + b информацию о положении прямой в координатной плоскости. Распознают параллельные и пересекающиеся прямые по их уравнениям; конструируют уравнения прямых, параллельных данной прямой. Используют приёмы самоконтроля при построении графиков линейных уравнений. Решают системы двух линейных уравнений с двумя переменными; используют графические представления для исследования систем линейных уравнений; решают простейшие системы, в которых одно из уравнений не является линейным. Применяют алгебраический аппарат для решения задач на координатной плоскости. Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решают составленную систему уравнений; интерпретируют результат | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом своих учебных и жизненных речевых ситуаций. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников |
|
| 104 | Контрольная работа №4 по теме: «Системы уравнений» | 1 | Линейное уравнение с двумя переменными. Графики уравнений вида: ax+by=c иax=by. Системы уравнений с двумя переменными. Задачи. | стр224 №1-11 | Определяют, является ли пара чисел решением уравнения с двумя переменными; приводят примеры решений уравнений с двумя переменными. Решают задачи, алгебраической моделью которых является уравнение с двумя переменными; находят целые решения путём перебора. Распознают линейные уравнения с двумя переменными; строят прямые – графики линейных уравнений; извлекают из уравнения вида у = kx + b информацию о положении прямой в координатной плоскости. Распознают параллельные и пересекающиеся прямые по их уравнениям; конструируют уравнения прямых, параллельных данной прямой. Используют приёмы самоконтроля при построении графиков линейных уравнений. Решают системы двух линейных уравнений с двумя переменными; используют графические представления для исследования систем линейных уравнений; решают простейшие системы, в которых одно из уравнений не является линейным. Применяют алгебраический аппарат для решения задач на координатной плоскости. Решают текстовые задачи алгебраическим способом: переходят от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решают составленную систему уравнений; интерпретируют результат | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - преобразовывают модели с целью выявления общих законов, определяющих предметную область. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее. | Объясняют самому себе свои отдельные ближайшие цели саморазвития; проявляют познавательный интерес к изучению математики; понимают причины успеха в учебной деятельности; дают адекватную оценку и самооценку учебной деятельности; анализируют соответствие результатов требованиям учебной задачи |
| Глава 5. Функции (19 часов) | 105 | Работа над ошибками. Чтение графиков | 1 | Графики функции. Графические характеристики - сравнение скоростей, вычисление скоростей, определение максимальных и минимальных значений. | Без домашнего задания | Читают графики реальных зависимостей | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - делают предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают социальную роль ученика, объясняют свои достижения |
|
| 106 | Что такое функция | 1 | Что такое функция. Зависимые, независимые переменны. Координаты. Абсцисса и ордината. Область определения функции. График функции. | п.5.1№727,728 | Вычисляют значения функций, заданных формулами (при необходимости используют калькулятор); составляют таблицы значений функций. Используют функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строят речевые конструкции с использованием функциональной терминологии | Регулятивные - составляют план выполнения заданий совместно с учителем.Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют уважительно относиться к позиции другого, договориться. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности |
|
| 107-108 | График функции | 2 | Зависимые, независимые переменны. Координаты. Абсцисса и ордината. Область определения функции. График функции. | п.5.2, №737-739 (б),740(б,г) | Строят по точкам графики функций. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют принимать точку зрения другого, слушать. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, адекватно оценивают результаты своей учебной деятельности, проявляют интерес к предмету |
|
| 109 | График функции | 1 | Зависимые, независимые переменны. Координаты. Абсцисса и ордината. Область определения функции. График функции. | п.5.3 №758 760,763 | Строят по точкам графики функций. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом своих учебных и жизненных речевых ситуаций. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников |
|
| 110 | Свойства функции | 1 | Свойства функции. Наибольшее и наименьшее значения функции. Положительные и отрицательные значения функции. Функция возрастает, убывает. | №766,770, 771 | Описывают свойства функции на основе её графического представления. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства получения информации. Познавательные - преобразовывают модели с целью выявления общих законов, определяющих предметную область. Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Проявляют познавательный интерес к изучению математики, способам решения учебных задач; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и сверстников; анализируют соответствие результатов требованиям учебной задачи |
|
| 111-112 | Исследование графика функции | 2 | Свойства функции. Наибольшее и наименьшее значения функции. Положительные и отрицательные значения функции. Функция возрастает, убывает. | п.5.4№778, 780(б,г), 781(б,г) | Описывают свойства функции на основе её графического представления. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, дают положительную оценку результатам своей учебной деятельности, проявляют интерес к предмету |
|
| 113 | Свойства функции. Самостоятельная работа №14 по теме: «Функция» | 1 | Свойства функции. Наибольшее и наименьшее значения функции. Положительные и отрицательные значения функции. Функция возрастает, убывает. | №782(б) 783(б),785 | Описывают свойства функции на основе её графического представления. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей | Регулятивные - определяют цель учебной деятельности, ищут средства ее осуществления. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют высказывать свою точку зрения и ее обосновать, приводя аргументы. | Объясняют самому себе свои наиболее заметные достижения, выражают положительное отношение к процессу познания, оценивают свою учебную деятельность |
|
| 114-115 | Свойства линейной функции | 2 | Определение линейной функции. График линейной функции. Свойства линейной функции. График постоянной функции. | №787,788 | Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Показывают схематически расположение на координатной плоскости графиков функций вида у = kx, у =kx + b в зависимости от значения коэффициентов, входящих в формулы. Строят графики изучаемых функций; описывают их свойства | Регулятивные - определяют цель учебной деятельности, ищут средства ее осуществления. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Принимают и осваивают социальную роль обучающегося; проявляют мотивы своей учебной деятельности; понимают личностный смысл учения |
|
| 116-117 | Линейная функция | 2 | Определение линейной функции. График линейной функции. Свойства линейной функции. График постоянной функции. | п.5.5№791,793 | Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Показывают схематически расположение на координатной плоскости графиков функций вида у = kx, у =kx + b в зависимости от значения коэффициентов, входящих в формулы. Строят графики изучаемых функций; описывают их свойства | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют понимать точку зрения другого. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 118-119 |
Свойства функции у = | 2 | Функция обратной пропорциональности. График функции. Свойства функции. | №795(б,г) 803(б,г) 801 | Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Показывают схематически расположение на координатной плоскости графиков функций вида в зависимости от значения коэффициентов, входящих в формулу у = | Регулятивные - составляют план выполнения заданий совместно с учителем. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом речевых ситуаций. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности |
|
| 120-121 | Свойства функции у = | 2 | Функция обратной пропорциональности. График функции. Свойства функции. | п.5.6 №813 815,817 | Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Показывают схематически расположение на координатной плоскости графиков функций вида в зависимости от значения коэффициентов, входящих в формулу у = | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - передают содержание в сжатом или развернутом виде. Коммуникативные - умеют высказывать свою точку зрения и пытаются ее обосновать, приводя аргументы. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
|
| 122 | Повторение по теме: «Функции» | 1 | Функции. Построение графика функций. Формулировка свойств функций. Чтение графиков. | №820,822 | Вычисляют значения функций, заданных формулами (при необходимости используют калькулятор); составляют таблицы значений функций. Строят по точкам графики функций. Описывают свойства функции на основе её графического представления. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей. Используют функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строят речевые конструкции с использованием функциональной терминологии. Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознают виды изучаемых функций. Показывают схематически расположение на координатной плоскости графиков функций вида у = kx, у =kx + b, у = | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее осуществления. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают роль ученика, объясняют свои достижения |
|
| 123 | Контрольная работа №5 по теме: «Функции» | 1 | Функции. Построение графика функций. Формулировка свойств функций. Чтение графиков. | стр 280-281 (1-10) | Вычисляют значения функций, заданных формулами (при необходимости используют калькулятор); составляют таблицы значений функций. Строят по точкам графики функций. Описывают свойства функции на основе её графического представления. Моделируют реальные зависимости формулами и графиками. Читают графики реальных зависимостей. Используют функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строят речевые конструкции с использованием функциональной терминологии. Используют компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознают виды изучаемых функций. Показывают схематически расположение на координатной плоскости графиков функций вида у = kx, у =kx + b, у = | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатов своей учебной деятельности |
| Вероятность и статистика (11 часов) | 124 | Анализ результатов контрольной работы. Работа над ошибками Статистические характеристики | 1 | Размах. Среднее арифметическое. Таблица частот. Мода. Медиана ряда. | Без домашнего задания | Характеризуют числовые ряды с помощью различных средних | Регулятивные - понимают причины своего неуспеха и находят способы выхода из этой ситуации. Познавательные - делают предположение об информации, которая нужна для решения учебной задачи. Коммуникативные - умеют критично относиться к своему мнению. | Объясняют самому себе свои наиболее заметные достижения |
|
| 125-126 | Вероятность равновозможных событий | 2 | Размах. Среднее арифметическое. Таблица частот. Мода. Медиана ряда. | п.6.1, №858(б,г) 861, 863 | Находят вероятность событий при равновозможных исходах | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют при необходимости отстаивать свою точку зрения, аргументируя ее, подтверждая аргументы фактами. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач |
|
| 127 | Вероятность равновозможных событий | 1 | Классическое определение вероятности. Способ вычисления вероятности события. | п.6.2, №872 №875 | Находят вероятность событий при равновозможных исходах | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее осуществления. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 128 | Сложные эксперименты | 1 | Классическое определение вероятности. Способ вычисления вероятности события. | №877, 878(в) №879, 880 | Решают задачи на вычисление вероятностей с применением комбинаторики | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют интерес к изучению предмета, дают положительную оценку и самооценку результатам деятельности |
|
| 129-130 | Сложные эксперименты | 2 | Классическое определение вероятности. Способ вычисления вероятности события. | п.6.3, №886 №888 | Решают задачи на вычисление вероятностей с применением комбинаторики | Регулятивные - обнаруживают и формулируют учебную проблему совместно с учителем. Познавательные - делают предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом речевых ситуаций. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 131-132 | Геометрические вероятности | 2 | Способ вычисления вероятности события. | №890,892 | Находят геометрические вероятности | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - сопоставляют и отбирают информацию, полученную из разных источников. Коммуникативные - умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают роль ученика, объясняют свои достижения |
|
| 133 | Повторение по теме: «Вероятность и статистика» | 1 | Классическое определение вероятности. Способ вычисления вероятности события. | п.6.4№ 894, №898,899 | Характеризуют числовые ряды с помощью различных средних. Находят вероятность событий при равновозможных исходах; решают задачи на вычисление вероятностей с применением комбинаторики. Находят геометрические вероятности | Регулятивные - в диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки. Познавательные - делают предположения об информации, которая нужна для решения предметной учебной задачи. Коммуникативные - умеют уважительно относиться к позиции другого, договариваться. | Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета |
|
| 134 | Контрольная работа №6 по теме: «Вероятность и статистика» | 1 | Размах. Среднее арифметическое. Таблица частот. Мода. Медиана ряда. Классическое определение вероятности. Способ вычисления вероятности события. | №910, стр306(1-4) | Характеризуют числовые ряды с помощью различных средних. Находят вероятность событий при равновозможных исходах; решают задачи на вычисление вероятностей с применением комбинаторики. Находят геометрические вероятности | Регулятивные - определяют цель учебной деятельности, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют слушать других, принимать другую точку зрения, изменять свою точку зрения. | Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, осознают и принимают роль ученика, объясняют свои достижения |
| Итоговое повторение за курс 8 класса (6 часов) | 135 | Итоговое повторение по теме: «Алгебраические дроби» | 1 | Основное свойство дроби. Преобразование выражений, содержащих алгебраические дроби. Степень с целым показателем. | стр 63-64 (1-18) | Конструируют алгебраические выражения. Находят область определения алгебраической дроби; выполняют числовые подстановки и вычисляют значение дроби, в том числе с помощью калькулятора. Выполняют действия алгебраических дробей. Применяют преобразование выражений для решения задач. Выражают переменные из формул (физических, геометрических, описывающих бытовые ситуации). Проводят исследования, выявляют закономерности. Формулируют, записывают в символической форме и иллюстрируют примерами свойства степени с целым показателем; применяют свойства степени для преобразования выражений и вычислений. Используют запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивают числа и величины, записанные с использованием степени 10. Выполняют вычисления с реальными данными. Выполняют прикидку и оценку результатов вычислений. Решают уравнения с дробными коэффициентами, решают текстовые задачи алгебраическим методом | Регулятивные - работают по составленному плану, используют наряду с основными и дополнительные средства. Познавательные - записывают выводы в виде правил «если …, то …». Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Объясняют самому себе свои отдельные ближайшие цели саморазвития, проявляют интерес к изучению предмета, дают положительную оценку и самооценку результатам деятельности Проявляют познавательный интерес к изучению математики, способам решения учебных задач; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и сверстников; анализируют соответствие результатов требованиям учебной задачи |
|
| 136 | Итоговое повторение по теме: «Квадратные корни» | 1 | Арифметический квадратный корень. Теоремы о корне из произведения и частного. Подобные радикалы. Равенство. Преобразования выражений, содержащих радикалы. Освобождение от иррациональности в знаменателе дроби. Формула дискриминанта квадратного уравнения, формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена
| стр 64-65 (1-16) стр 119-120 (1-20) | Формулируют определения квадратного корня из числа, решают задачи, приведшие к понятию квадратного корня. Приводят примеры иррациональных чисел; распознают иррациональные и рациональные числа. Описывают множество действительных чисел. Изображают числа точками координатной прямой. Формулируют теорему Пифагора, умеют находить любую сторону прямоугольного треугольника, если известны две другие. Строят график функции у = | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют организовывать учебное взаимодействие в группе. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников |
|
| 137-138 | Итоговая контрольная работа за курс 8 класса | 2 | Основной теоретический материал за курс 8 класса. | стр281-283 (1-15) | Находят область определения алгебраической дроби; выполняют числовые подстановки и вычисляют значение дроби, в том числе с помощью калькулятора. Выполняют действия алгебраических дробей. Строят графики функций у = | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом ситуаций. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников |
|
| 139-140 | Анализ контрольной работы. Работа над ошибками. Задание на лето. | 2 | Основной теоретический материал за курс 8 класса. | Без дом. задания | Анализ типичных ошибок, их исправление. Получают задание на лето. | Регулятивные - определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств ее достижения. Познавательные - передают содержание в сжатом, выборочном или развернутом виде. Коммуникативные - умеют оформлять свои мысли в устной и письменной речи с учетом ситуаций. | Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; |





