
«Я слышу и забываю,
Я вижу и запоминаю,
Я делаю и я понимаю»
( Конфуций )

Повторение изученного материала
Параллелогр.
1. Противолежащие стороны параллельны и равны
Прямоугол.
2. Все стороны равны
Ромб
3. Противолежащие углы равны, сумма соседних углов равна 180 о
Квадрат
4. Все углы прямые
5. Диагонали пересекаются и точкой пересечения делятся пополам
6. Диагонали равны
7. Диагонали взаимно перпендикулярны и являются биссектрисами углов

Повторение изученного материала
1. Любой ромб является…
а) квадратом; в) параллелограммом;
б) прямоугольником; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник…
а) ромб; в) прямоугольник;
б) квадрат; г) нет правильного ответа.
3.Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм…
а) ромб; в) прямоугольник;
б) квадрат; г) нет правильного ответа .
4. Прямоугольник – это четырехугольник, в котором…
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
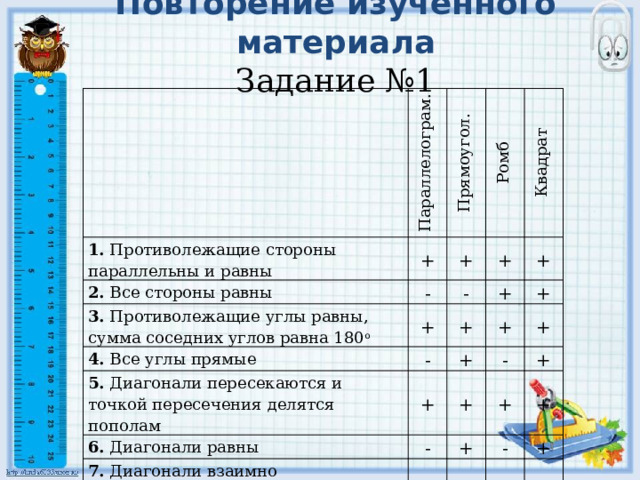
Повторение изученного материала Задание №1
Параллелограм.
1. Противолежащие стороны параллельны и равны
Прямоугол.
+
2. Все стороны равны
-
Ромб
+
3. Противолежащие углы равны, сумма соседних углов равна 180 о
+
4. Все углы прямые
-
+
Квадрат
+
+
-
+
5. Диагонали пересекаются и точкой пересечения делятся пополам
+
+
+
6. Диагонали равны
+
-
+
+
-
7. Диагонали взаимно перпендикулярны и являются биссектрисами его углов
+
+
+
-
+
-
-
+
+
+

Задание №2
1. Любой ромб является…
а) квадратом; в) параллелограммом;
б) прямоугольником; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник…
а) ромб; в) прямоугольник;
б) квадрат; г) нет правильного ответа.
3.Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм…
а) ромб; в) прямоугольник;
б) квадрат; г) нет правильного ответа.
4. Прямоугольник – это четырехугольник, в котором…
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в) два угла прямые и две стороны равны

Критерии оценивания:
«5» - не более 2 ошибок
«4» - не более 4 ошибок
«3» - от 4 до 7 ошибок
«2» – более 7 ошибок

Лучевая
- Расположение частей тела, позволяющее разделить его на 2 равные, зеркально отражающие друг друга половины в нескольких плоскостях.

Билатеральная (осевая)
- Расположение частей тела, позволяющее разделить его на две равные, зеркально отражающие друг друга половины лишь одной плоскостью. Эта плоскость носит название оси симметрии.
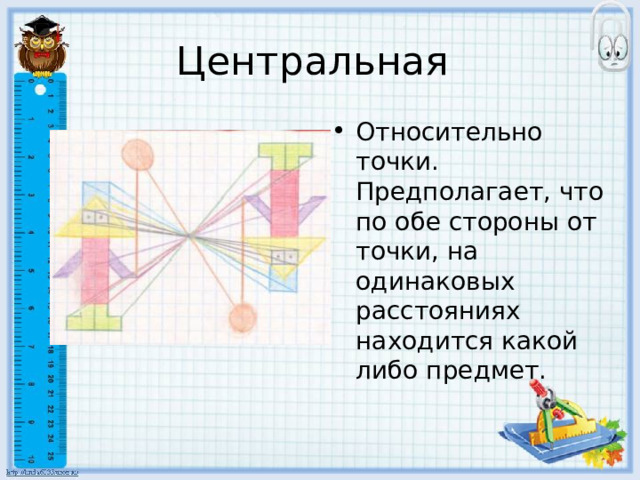
Центральная
- Относительно точки. Предполагает, что по обе стороны от точки, на одинаковых расстояниях находится какой либо предмет.

Зеркальная
- Зеркальная в архитектуре и природе. Отражение прибрежных зданий. Оптическое отражение в реке прибрежных деревьев. Отражение свечи в зеркале.

Подобие
- Представляет собой своеобразные аналогии предыдущих с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними.

Архитектура
- Особенно блистательно использовали в архитектурных сооружениях древние зодчие. В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты


Техника
- В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью в работе.


Искусство
- Как бы ни развивалось в дальнейшем искусство, элементы в нем все же будут преобладать

В одежде

Русский язык и ……… слов и чисел
- Вертикальная ось ……: А; Д; Л; М; П; Т; Ф; Ш. Горизонтальная ось ……: В; Е; З; К; С; Э; Ю. И вертикальные, и горизонтальные оси ……: Ж; Н; О; Х. Ни вертикальные, ни горизонтальные оси: Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я.
- В русском языке есть слова – палиндромы, которые можно читать одинаково в двух направлениях: Шалаш, казак, радар, Алла, Анна, кок, поп.

в быту

в природе
- Ярко выраженно обладают листья, ветви, цветы, плоды. Форма листа дерева не является случайной: она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок, одна из которых расположена зеркально относительно другой. листк упорно повторяется, будь то гусеница, бабочка, жучок и т.п.



в животном мире


в музыке

в декоративно-прикладном творчестве
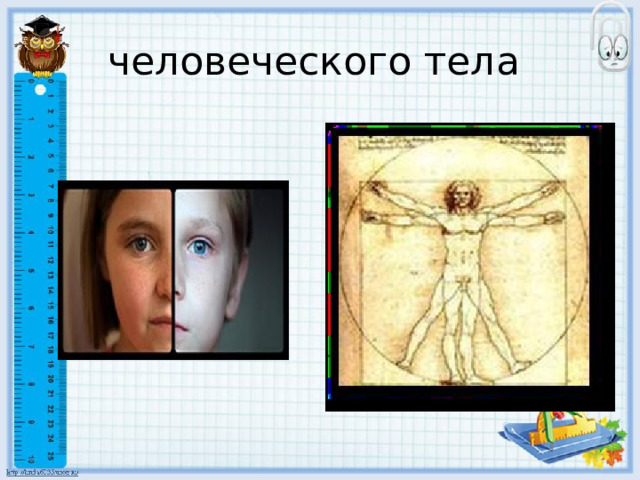
человеческого тела

Времена года

Семья

Тема урока:

СИММЕТРИЯ
(осевая и центральная)
Тема урока:

Симметрия - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости.
(толковый словарь русского языка Ожегова)
«Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».
Г. Вейль
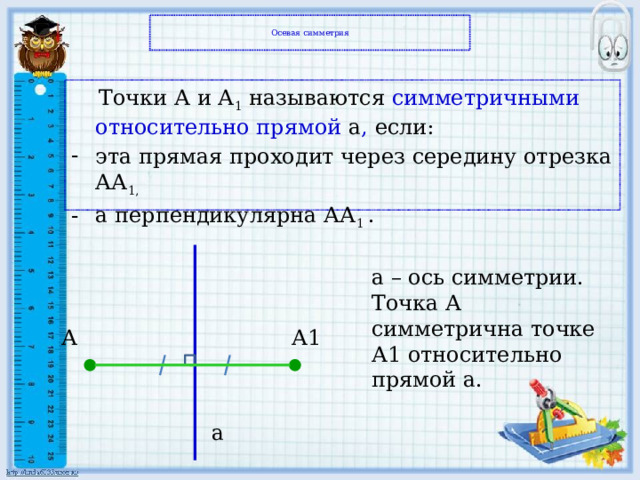
Осевая симметрия
Точки А и А 1 называются симметричными относительно прямой а , если:
- эта прямая проходит через середину отрезка АА 1,
- а перпендикулярна АА 1 .
a – ось симметрии.
Точка А симметрична точке А1 относительно прямой а.
А
А1
а
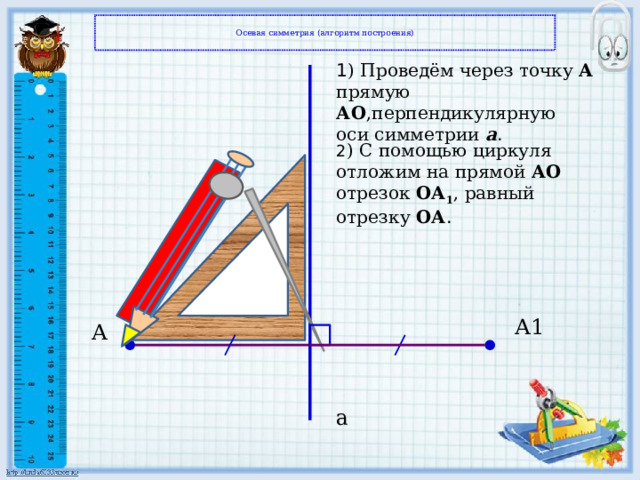
Осевая симметрия (алгоритм построения)
1 ) Проведём через точку А прямую АO ,перпендикулярную оси симметрии a .
2 ) С помощью циркуля
отложим на прямой АO отрезок OА 1 , равный отрезку OА .
А1
А
а
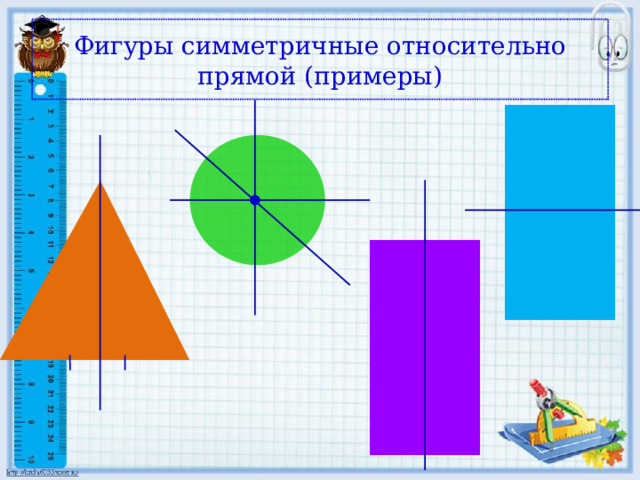
Фигуры симметричные относительно прямой (примеры)
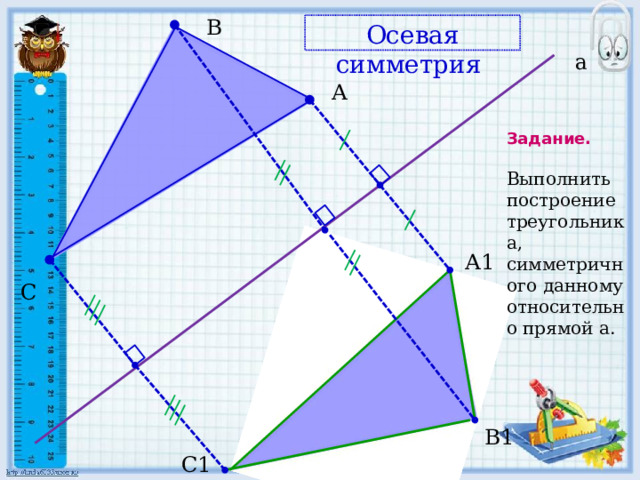
B
Осевая симметрия
а
А
Задание. Выполнить построение треугольника, симметричного данному относительно прямой a.
A1
C
B1
C1
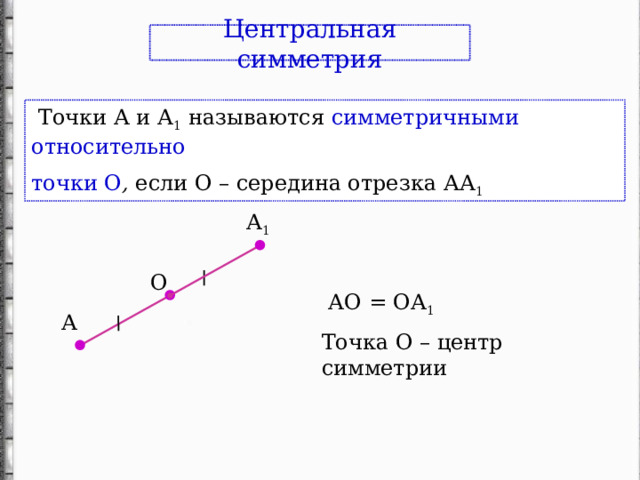
Центральная симметрия
Точки А и А 1 называются симметричными относительно
точки О , если О – середина отрезка АА 1
А 1
О
АО = ОА 1
Точка О – центр симметрии
А
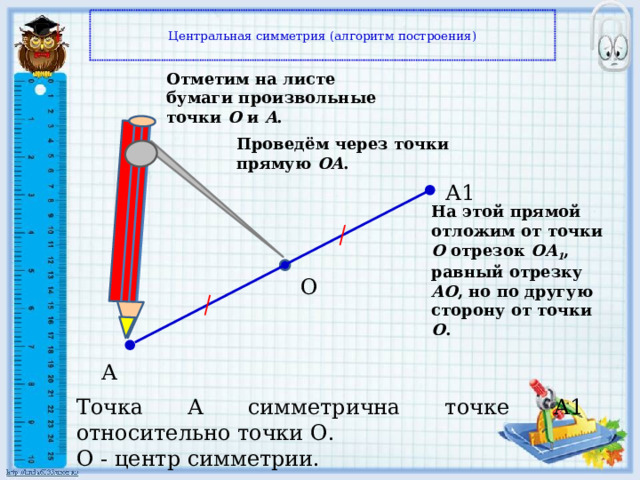
Центральная симметрия (алгоритм построения)
Отметим на листе бумаги произвольные точки O и A .
Проведём через точки прямую OA .
А1
На этой прямой отложим от точки O отрезок OA 1 , равный отрезку AO , но по другую сторону от точки O .
О
А
Точка А симметрична точке А1 относительно точки О.
О - центр симметрии.
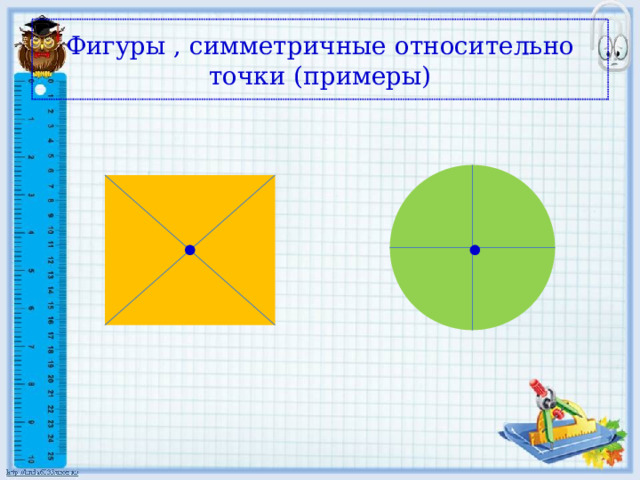
Фигуры , симметричные относительно точки (примеры)
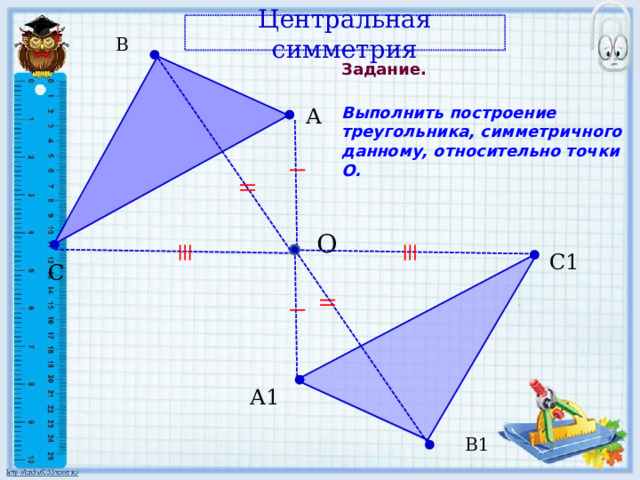
Центральная симметрия
В
Задание.
Выполнить построение треугольника, симметричного данному, относительно точки O.
А
О
С1
С
А1
В1

О симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза.
И снежный рой - творение мороза.

Домашнее задание:
Вопросы 16 – 20 стр. 115,
№ 417, 423;
подготовить информацию о симметрии в….





