Презентация к уроку алгебры и началам анализа в 11 классе на тему: " Применение производной для исследования функций на монотонность и экстремумы"

Применение производной для исследования функций на монотонность и экстремумы

• Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков монотонности функции ( промежутков возрастания и убывания ). Такой анализ легко сделать с помощью производной.

• Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей , если большему значению аргумента соответствует меньшее значение функции.

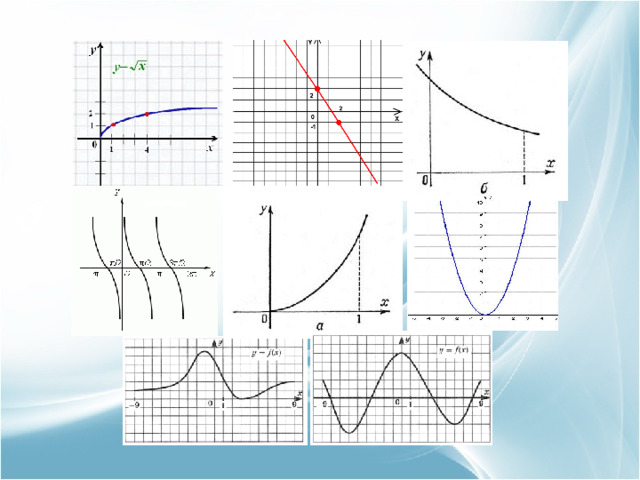
убывающая

убывающая

убывающая

возрастающая

возрастающая

возрастающая и убывающая на интервалах

возрастающая и убывающая на интервалах

возрастающая и убывающая на интервалах

Теорема 1.

• Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Теорема 2.

• Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает) .

Правило нахождения интервалов монотонности

• Находим область определения функции f(x) .
• Вычисляем производную f’(x) данной функции.
• Находим точки, в которых f’(x) =0 или не существует. Эти точки называются критическими для функции f(x).
• Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности .
• Исследуем знак f’(x) на каждом интервале. Если f’(x)› 0 , то на этом интервале f ( x) возрастает ; если f’(x)‹ 0 , то на таком интервале функция f(x) убывает .

Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5

• Область определения : R . Функция непрерывна.
• Вычисляем производную : y’=6x²-6x-36.
• Находим критические точки: y’= 0.

x²-x-6 =0

Д=1-4*(-6)*1=1+24=25

• Делим область определения на интервалы:
• Функция возрастает при x ϵ (-∞;-2] υ [3;+∞) , функция убывает при x ϵ [ -2;3 ] .

-

+

+

-2

3

Пример №2. Найти промежутки монотонности функции y=x³-3x²

• Область определения : R . Функция непрерывна.
• Вычисляем производную : y’= 3 x²-6x.
• Находим критические точки: y’= 0.

x²- 2 x =0

x(x-2)=0

x1=0 и x2=2

• Делим область определения на интервалы:
• Функция возрастает при x ϵ (-∞;0] υ [2;+∞) , функция убывает при x ϵ [0 ; 2] .

+

-

-

0

2

• Точку x 0 называют точкой минимума функции y=f(x) , если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x 0 ) .
• Точку x 0 называют точкой максимума функции y=f(x) , если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x 0 ) .

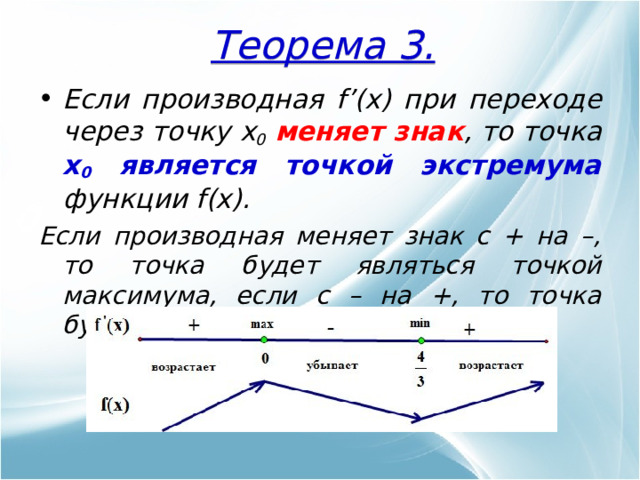
Теорема 3.

• Если производная f ’( x ) при переходе через точку x 0 меняет знак , то точка x 0 является точкой экстремума функции f ( x ).

Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума

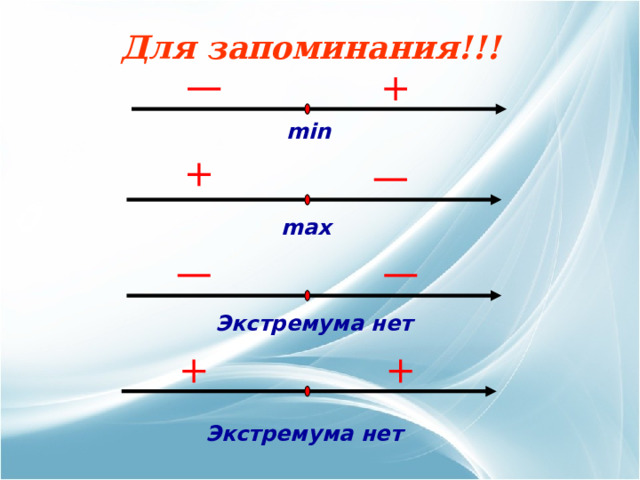
Для запоминания!!!

min

max

Экстремума нет

Экстремума нет

Пример № 3 . Найти экстремумы функции y= - 2x³-3x² +12 x -4

• Область определения : R . Функция непрерывна.
• Вычисляем производную : y’= - 6x²-6x +12 .
• Находим критические точки: y’= 0.

- x²-x +2=0

Д=1-4*(-1)*2=1+8=9

x 1 =1; x 2 =-2

• Делим область определения на интервалы:
• x =-2 – точка минимума . Найдём минимум функции y min =-24 . x =1 – точка максимума . Найдём максимум функции: y max =3 .

+

-

-

-2

1

Работа на уроке:

• Исследовать на экстремум функцию y=x 2 +2.

Решение:

• Находим область определения функции: D(y)=R.
• Находим производную: y’=(x 2 +2)’=2x.
• Приравниваем её к нулю: 2x=0 , откуда x=0 – критическая точка.
• Делим область определения на интервалы и определяем знаки производной на каждом интервале:
• x =0 – точка минимума. Найдём минимум функции y min =2.

-

+

0

• Исследовать на экстремум функцию y= 1/3 x 3 -2 x 2 +3 x+1.

Решение:

• Находим область определения функции: D(y)=R.
• Находим производную: y’=( 1/3 x 3 -2 x 2 +3 x+1)’=x 2 -4x+3.
• Приравниваем её к нулю: x 2 -4x+3=0 , откуда x 1 =1, x 2 =3 – критические точки.
• Делим область определения на интервалы и определяем знаки производной на каждом интервале:
• x =1 – точка максимума. Найдём максимум функции y max =7/3. x =3 – точка минимума. Найдём минимум функции: y min =1 .

-

+

+

1

3

• Исследовать на экстремум функцию y=x 3 +3 x 2 +9 x -6 .

Решение:

• Находим область определения функции: D(y)=R.
• Находим производную: y’=(x 3 +3 x 2 +9 x -6 )’= 3 x 2 +6 x+ 9 .
• Приравниваем её к нулю: 3 x 2 +6 x+ 9=0, откуда D
• Однако, функция возрастает на всей D(y) , так как y’= 3 x 2 +6 x+ 9 0 :

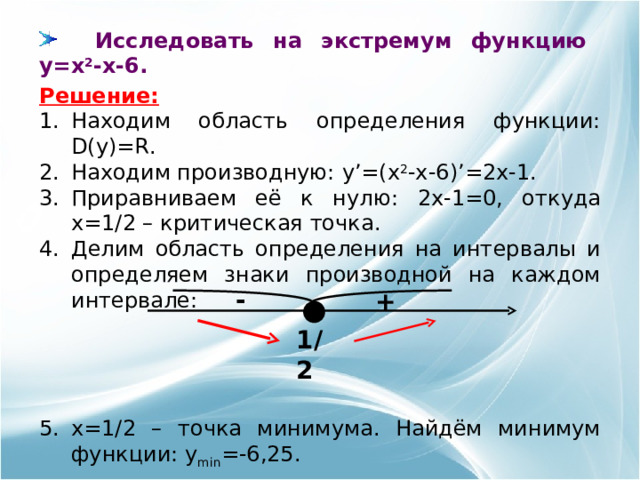
• Исследовать на экстремум функцию y=x 2 -x-6.

Решение:

• Находим область определения функции: D(y)=R.
• Находим производную: y’=(x 2 -x-6)’=2x-1.
• Приравниваем её к нулю: 2x-1=0 , откуда x=1/2 – критическая точка.
• Делим область определения на интервалы и определяем знаки производной на каждом интервале:
• x =1/2 – точка минимума. Найдём минимум функции: y min =-6,25 .

-

+

1/2

Выполнить задания:

Пример: Исследовать функцию на монотонность и экстремумы

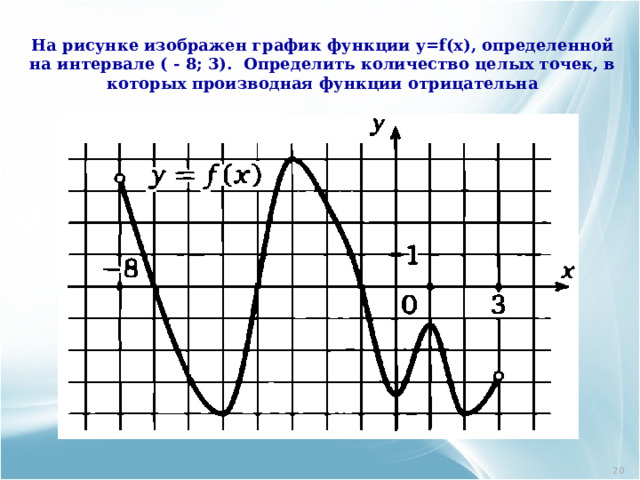
На рисунке изображен график функции y=f(x) , определенной на интервале ( - 8; 3). Определить количество целых точек, в которых производная функции отрицательна

17

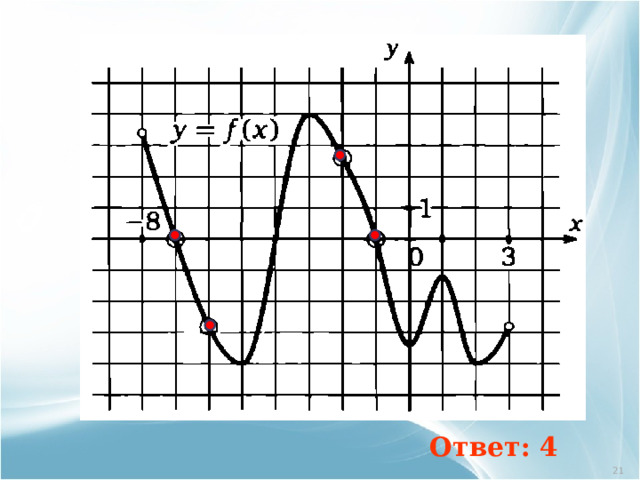
Ответ: 4

17

На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 7; 5). Найти точку экстремума функции на отрезке [ -6 ; 4]

17

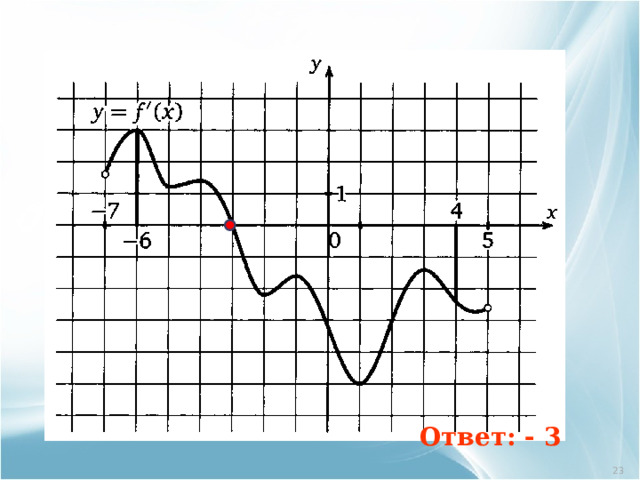
Ответ: - 3

17

На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 3; 8). Найти количество точек максимума функции на отрезке [ - 2 ; 7 ]

17

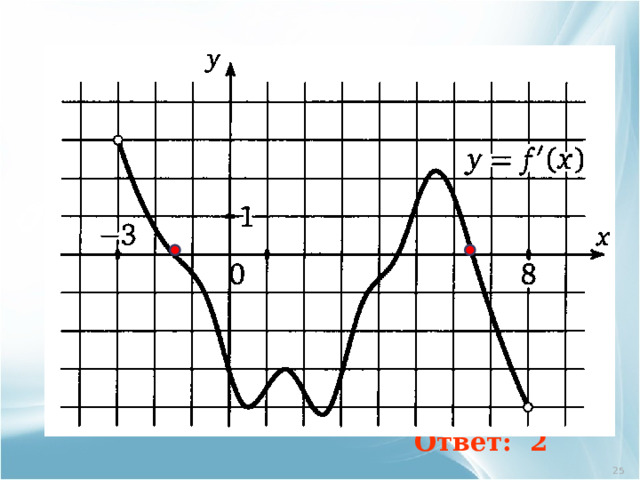
Ответ: 2

17

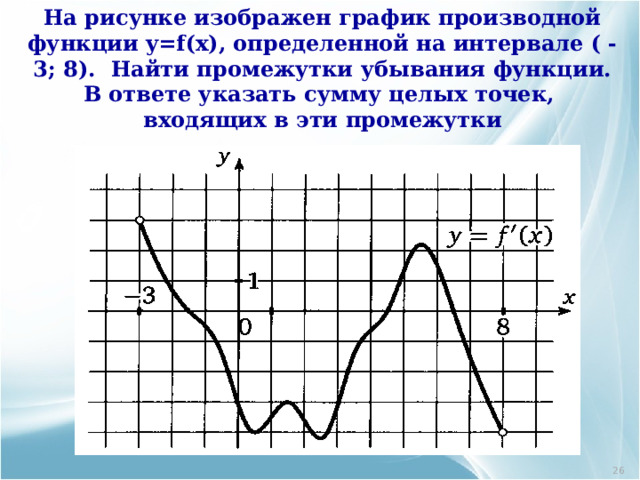
На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 3; 8). Найти промежутки убывания функции. В ответе указать сумму целых точек, входящих в эти промежутки

17

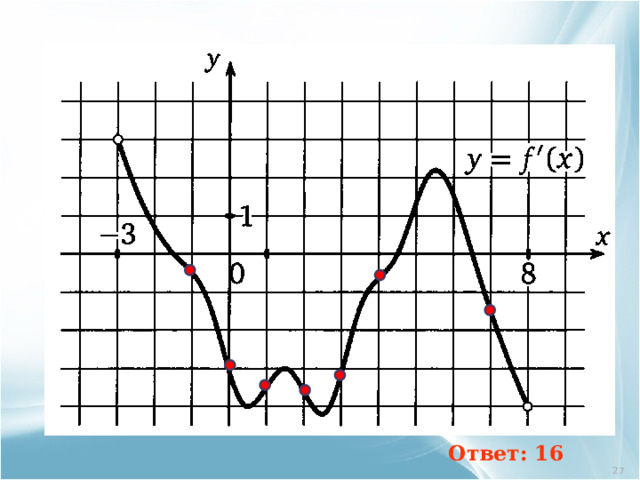
Ответ: 16

17

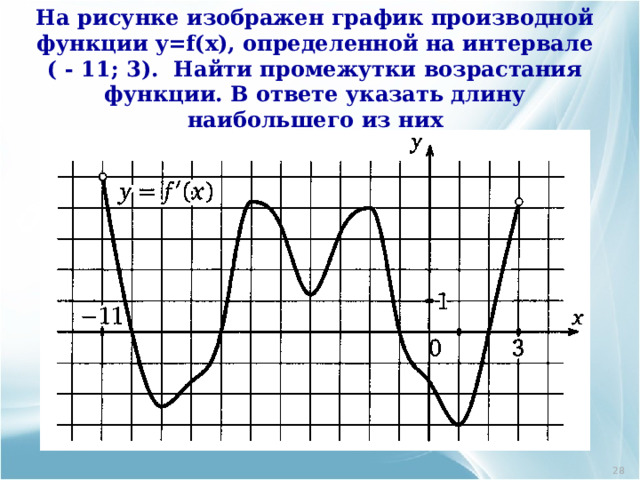
На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 11; 3). Найти промежутки возрастания функции. В ответе указать длину наибольшего из них

17

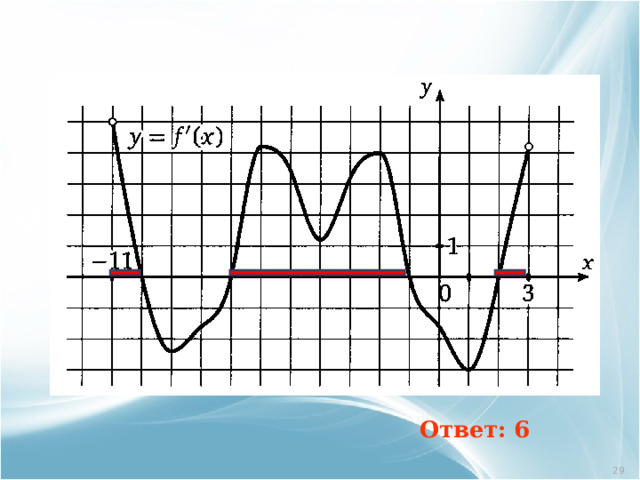
Ответ: 6

17

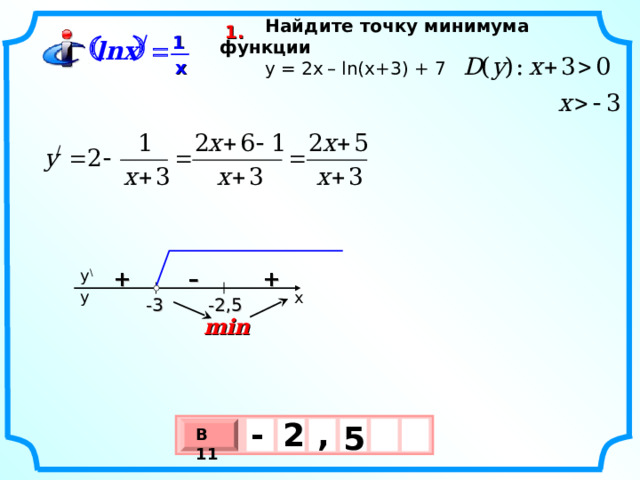
Найдите точку минимума функции

y = 2х – ln ( x +3) + 7

1.





1

/

lnx



x

+

+

y \

–

y

x

-3

-2,5

min

-

,

2

5

В 11

х

3

х

1

0

Найдите точку минимума функции

2.





/



/

/



uv

v

u

uv

–

–

+

y \

y

x

8

2

min

2

В 11

х

3

х

1

0

Найдите точку максимума функции

3.

/





1

1









х

2

х





Запишем функцию в удобном для дифференцирования виде

–

+

+

–

y \

y

x

0

17

-17

max

1

7

В 11

х

3

х

1

0

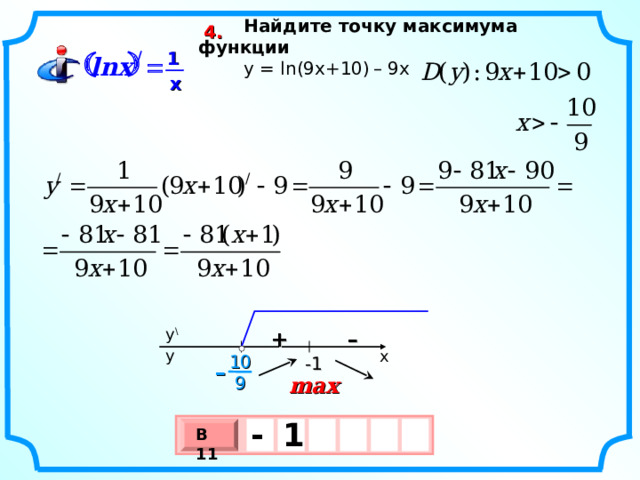
Найдите точку максимума функции

y = ln (9 x +10) – 9х

4.





1

/

lnx



x

y \

–

+

y

x

10

-1

–

9

max

-

1

В 11

х

3

х

1

0