
Тема: Определение числовой функции и способы её задания

Цели :
- Повторение и обобщение основных сведений о функции, полученных в 7-9 кл.
- Развитие навыков работы с графиками функций.
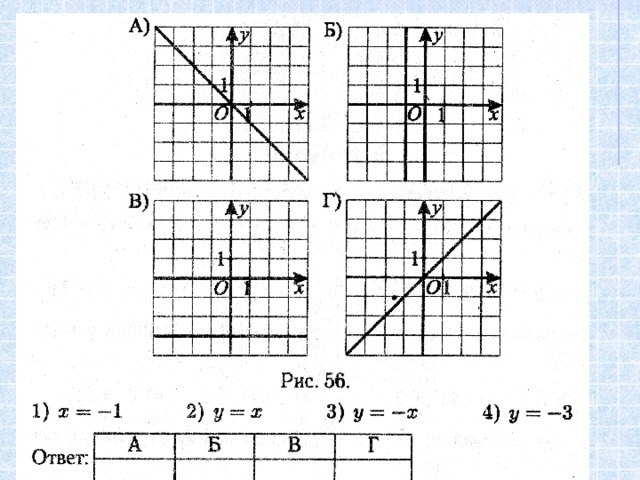
Вычислите:
Упростите:
а) –х+2,5х+у
б)
в)
а) -3,6+1,02
б) -8,19+(-2,01)
в) 0,5-3
г) -0,07∙1,2
д) -0,8:(-0,16)
е) -3,46∙1,3+1,46∙1,3



Определение функции:
Если даны числовое множество Х
и правило f , позволяющее поставить в соответствие
каждому элементу х из множества Х
единственное число у,
то говорят, что задана функция y=f(x)
с областью определения Х
Обозначение функции:
у=f(x), хє Х
у=g(x), хє Х
у=φ(x), хє Х
…
х – независимая переменная
f
у – зависимая переменная
Х
Х
f(x)
у
у1

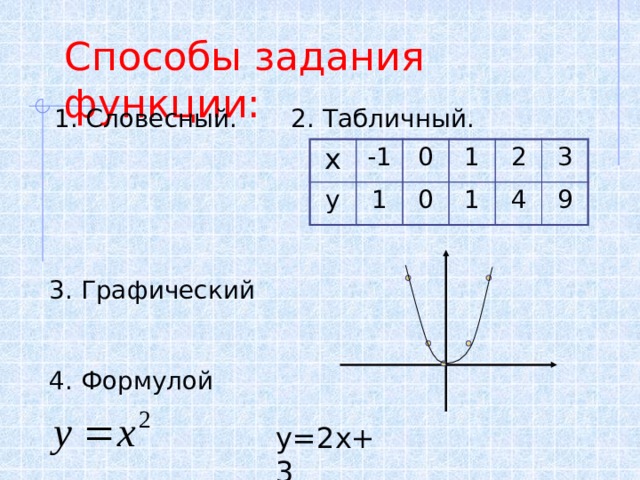
Способы задания функции:
2. Табличный.
1. Словесный.
х
-1
у
1
0
1
0
1
2
3
4
9
3. Графический
4. Формулой
у=2х+3
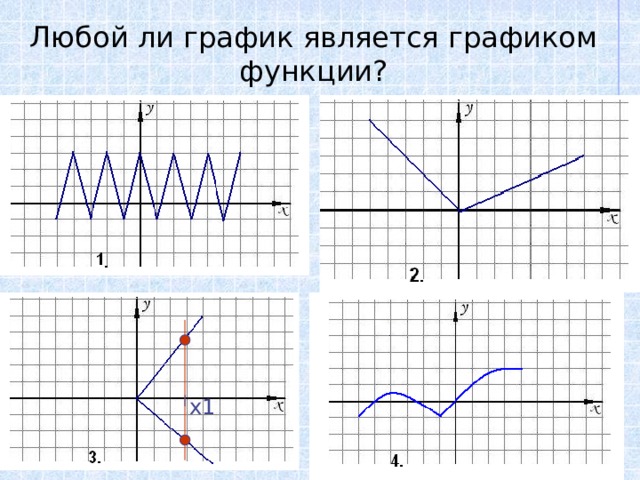
Любая ли формула задает функцию?
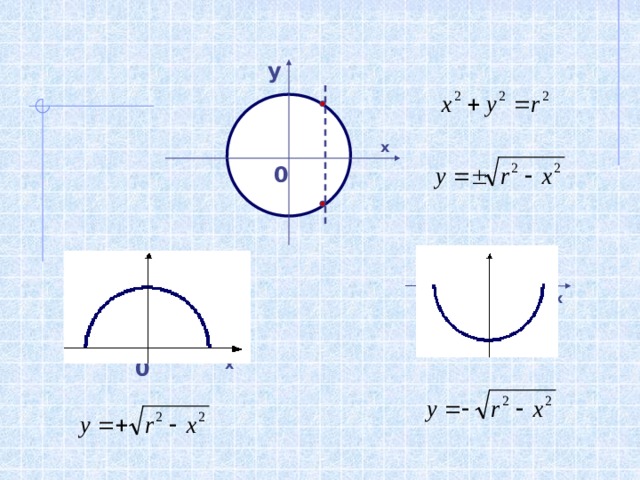
Любой ли график является графиком функции?
х1

у
x
0
у
у
x
0
0
x
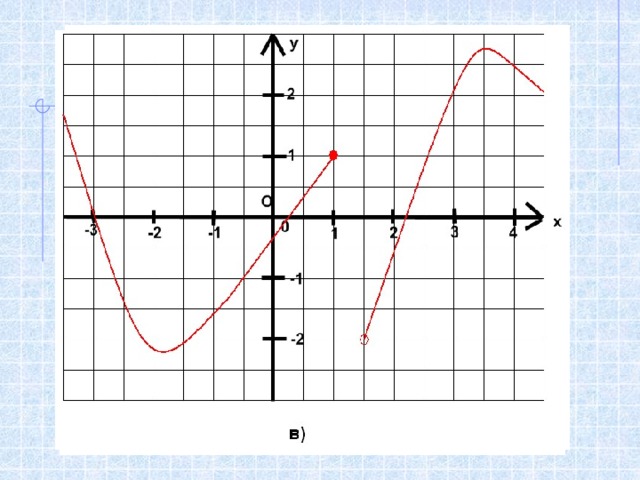
Область определения функции
Областью определения функции называют множество всех значений, которые принимает независимая переменная (х)
D(f)=(-∞;+∞)
Обозначение:
D(f)
Х
D(f)=(-∞;-1)U(-1;+∞)
D(f)=[3;+∞)

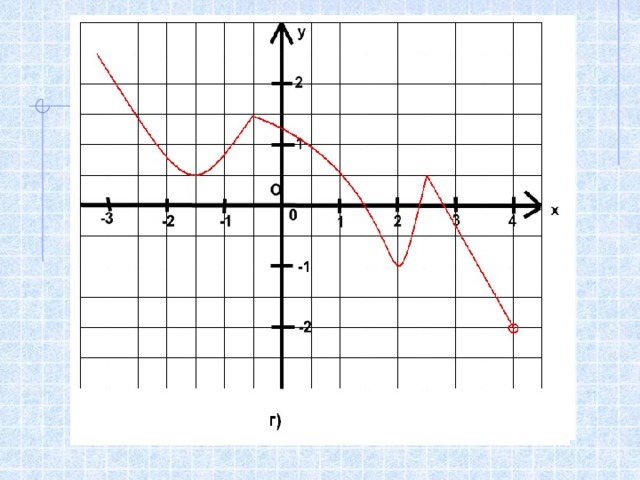
Область значений функции
Областью значений функции называют множество всех значений , которые принимает зависимая переменная (у)
E(f)=[0;+∞)
Обозначение: Е(f)
E(f)=(-∞;0)U(0;+∞)
E(f)=[0;+∞)

Историческая справка
Готфрид Вильгельм Лейбниц.
( 1646—1716 ), немецкий философ, математик, юрист, историк. Сделал первые попытки описания функции. Сам термин «функция» принадлежит Лейбницу и происходит от латинского слова function, что означает
«выполнение», «осуществление».
Историческая справка
Готфрид Вильгельм Лейбниц.
Начиная с 1698 года, Лейбниц
ввел также термины «перемен-
ная» и «константа». В 18 веке
появляется новый взгляд на
функцию как на формулу, свя-
зывающую одну переменную с
другой. Это так называемая ана-
литическая точка зрения на понятие функции.
Подход к такому определению впервые сделал
швейцарский математик Иоганн Бернулли (1667-1748 )





