Практические занятия по электротехнике

Практическое занятие № 1

Расчет величин сопротивления, электроемкости и ЭДС при параллельном, последовательном и смешанном соединении.

Цель:- Закрепить знания по теме;

- сформировать умения и навыки нахождения величин, вывод величин из формул.

Теория:

Сопротивление проводника, Ом,

,

где ρ – удельное сопротивление, Ом·мм²/ м; γ –удельная проводимость, м/( Ом·мм²);l_ длина проводника, м; S- сечение проводника, мм².

Соединение элементов электрической цепи

Соединение сопротивлений

Электрическая цепь может содержать несколько приемников энергии, имеющих различные сопротивления.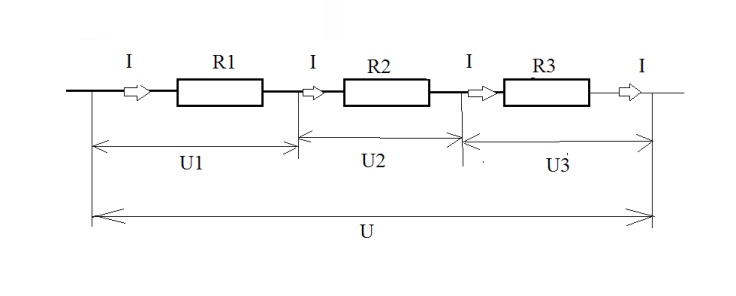 

А) последовательное соединение

I₁ = I₂ = I₃ = ······ = I  

U = U₁ + U₂ + U₃     

Для  n последовательно включённых проводников:

 R = R₁ + R₂ + R₃ +······+ R_n   

Б) Параллельное соединение.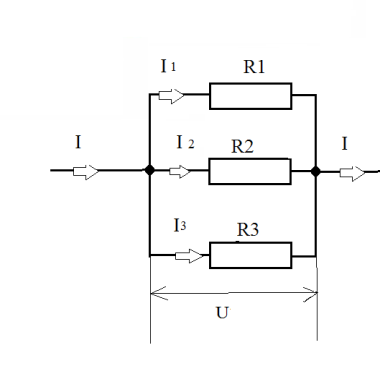

I = I₁ + I₂ + I₃   

U₁ = U₂ = U₃ = U 

 Если имеем  n параллельно соединённых проводников, имеющих одинаковое сопротивление R₁, то общее сопротивление цепи:

Соединение конденсаторов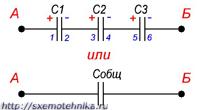

А) последовательное

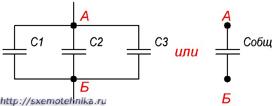
Б) Параллельное соединение конденсаторов.

Соединение источников тока

А) Последовательное соединение источников: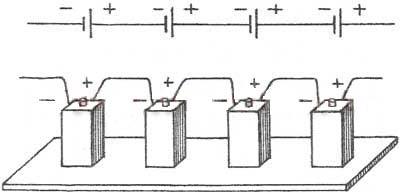  

Е= E n, а r₀= r n . 

Тогда з-н Ома запишется в виде:

I=

Б) параллельное соединение

ЭДС батареи при параллельном соединении равна ЭДС одного аккумулятора: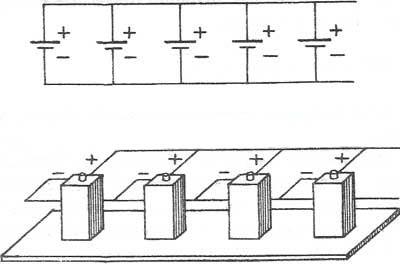

Е_б= Е₁=Е₂=Е₃=….

Ток, отдаваемый батареей в сеть, будет

 

Решить задачи:

3.1 Три проволочных сопротивления соединены последовательно: R1 = 180 Ом, R2 = 20 Ом, R3 = 80 Ом. Определить ток в цепи и падение напряжения на каждом сопротивлении, если к ним присоединен источник тока с напряжением U = 40 В. Внутреннее сопротивление батареи r₀ = 0.

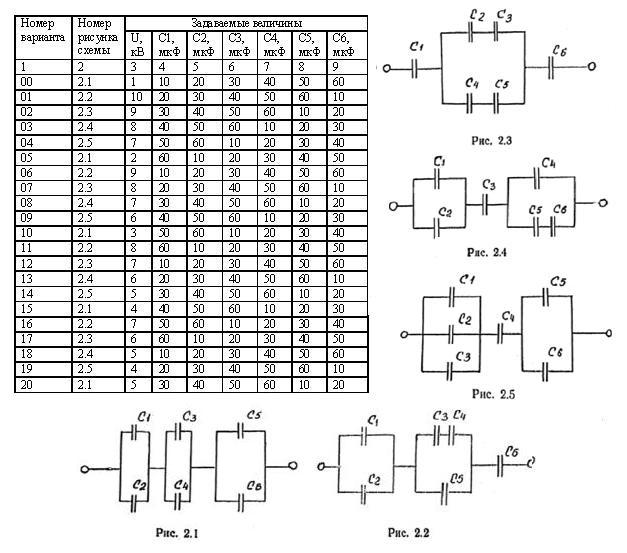
3.2. Определить эквивалентное сопротивление на зажимах АВ схемы рис. 2.2, где R1=0,5 Ом, R2=5 Ом. R3=9 Ом.

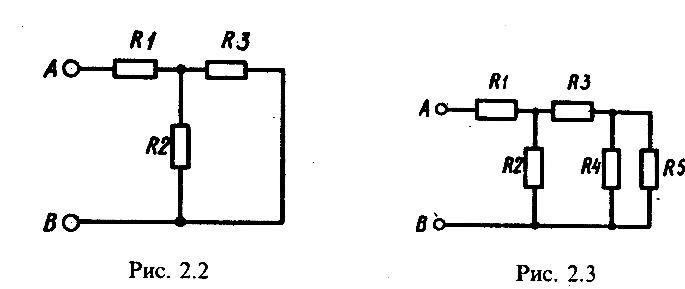
3.3. Определить эквивалентное сопротивление электрической цепи, представленной на рис.2.3, если R1=2,5 Ом, R2=6 Ом, R3=2 Ом, R4=1,5 Ом, R5=3 Ом.

3.4. На рис. 2.4 представлена схема электрической - цепи, где R1= R2 =15 Ом, R3 = R6 = 20 Ом, R4=R5=17,5 Ом, R7=12 Ом. Определить, эквивалентное сопротивление цепи между зажимами.

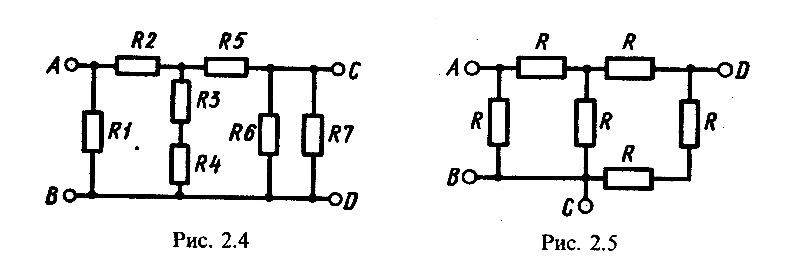
3.5. Определить в общем виде сопротивление электрической цепи, представленной на рис. 2.5, относительно зажимов АВ, ВС, CD.

3.6. В схеме рис.2.6 значения сопротивлений резисторов одинаковы и равны R. Определить в общем виде значения сопротивлении между зажимами АВ, АС, AD, CD, ЕЕ.

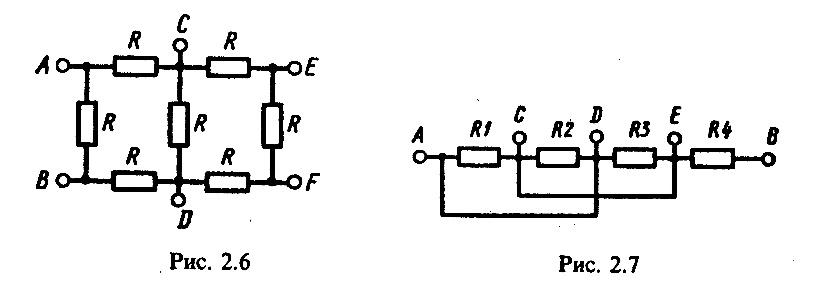
3.7. Для электрической цепи, представленной на рис. 2.7, определить сопротивления на участках цепи AB, DE и AE в общем виде, R1=R2=R3=R4=R.

3.8. При заданных проводимостях четырех параллельных ветвей G₁=0,11 Ом^-1; G₂=0,03 Ом^-1; G₃ = 0,07 Ом^-1; G ₄=0,04 Ом^-1 определить эквивалентную проводимость и эквивалентное сопротивление цепи.

3.9. Для электрической цепи, представленной на рис.2.10, определить общую проводимость цепи, если R1= 25 Ом, R2 = 50 Ом, R3 = 40 Ом и R 4=60 Ом.

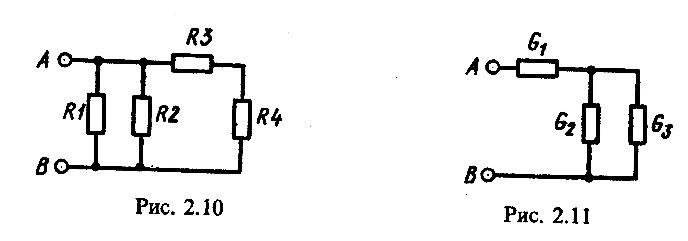
3.10. В схеме электрической цепи, представленной на рис. 2.11, задано значениеэквивалентной проводимости цепи G=0,025 Ом^-1. Определить проводимость G₁, если G₂=0,01 Ом^-1, G₃=0,04 Ом^-1.

3.11. Определить проводимости G ₂ и- G ₃ электрической цепи, представленной на рис.2.12, если G₁=0,05 Ом^-1, G₄=0,2 Ом^-1, G₅=0,1 Ом^-1и G = 0,17 Ом^-1. Проводимости G ₂=G ₃.

Практическая работа №2

Тема: Расчет электрической цепи со смешанным соединением конденсаторов.

Цель: Изучить методы соединения конденсаторов в электрических цепях постоянного тока. Рассчитать эквивалентную емкость, напряжение и заряд батареи конфденсаторов при смешанном соединении конденсаторов.

Ход работы:

1. Изучить свойства конденсаторов, способы соединения, формулы для определения основных величин.

2. Рассчитать эквивалентную емкость, напряжение и заряд батареи конденсаторов при смешанном соединении конденсаторов по заданному варианту.

3. Оформить отчет.

Теоретическая часть:

Сообщение электрического заряда проводнику называется электризацией. Чем больший заряд принял проводник, тем больше его электризация, или, иначе говоря, тем выше его электрический потенциал.

Между количеством электричества и потенциалом данного уединенного проводника существует линейная зависимость: отношение заряда проводника к его потенциалу есть величина постоянная:

Для какого-либо другого проводника отношение заряда к потенциалу есть также величина постоянная, но отличная от этого отношения для первого проводника.

Одной из причин, влияющих на эту разницу, являются размеры самого проводника. Один и тот же заряд, сообщенный различным проводникам, может создать различные потенциалы. Чтобы повысить потенциал какого-либо проводника на одну единицу потенциала, необходим определенный заряд. 

Свойство проводящих тел накапливать и удерживать электрический заряд, измеряемое отношением заряда уединенного проводника к его потенциалу, называется электрической емкостью, или просто емкостью, и обозначается буквой С.

Приведенная формула позволяет установить единицу емкости.

Практически заряд измеряется в кулонах, потенциал в вольтах, а емкость в фарадах:

Емкостью в 1 фараду обладает проводник, которому сообщают заряд в 1 кулон и при этом потенциал проводника увеличивается на 1 вольт.

Единица емкости — фарада (обозначается ф или F) очень велика. Поэтому чаще пользуются более мелкими единицами — микрофарадой (мкф или  ), составляющей миллионную часть фарады:

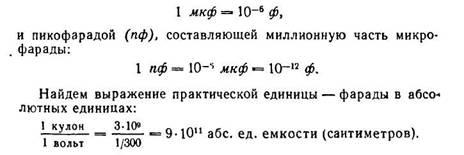
Устройство, предназначенное для накопления электрических зарядов, называется электрическим конденсатором. Конденсатор состоит из двух металлических пластин (обкладок), разделенных между собой слоем диэлектрика. Чтобы зарядить конденсатор, нужно его обкладки соединить с полюсами электрической машины. Разноименные заряды, скопившиеся на обкладках конденсатора, связаны между собой электрическим полем. Близко расположенные пластины конденсатора, влияя одна на другою, позволяют получить на обкладках большой электрический заряд при относительно невысокой разности потенциалов между обкладками. Емкость конденсатора есть отношение заряда конденсатора к разности потенциалов между его обкладками:

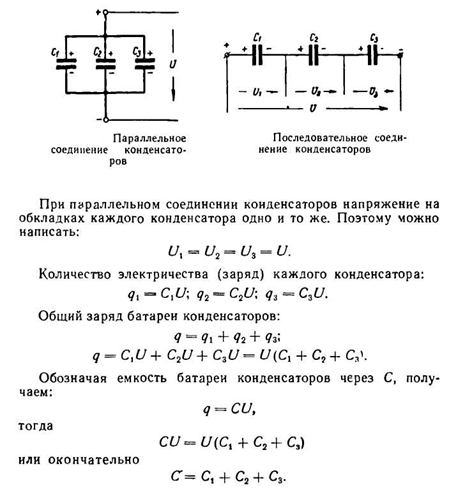
Следовательно, при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. При параллельном соединении каждый конденсатор окажется включенным на полное напряжение сети.

Рассмотрим последовательное соединение конденсаторов:

Практическое задание:

Определить заряд, напряжение, энергию электрического поля каждого конденсатора, эквивалентную емкость цепи.

 

 

Электрические цепи постоянного тока и методы их расчета

Практические занятия проводятся с целью успешного освоения студентами теоретического материала и применения его для решения задач и анализа полученных результатов. На практических занятиях №1 и №2 подробно рассмотрены примеры расчета электрических цепей с помощью различных методов, показано, как надо проверять правильность решения задачи и проанализированы возможные режимы работы всей цепи и отдельных ее элементов.

Практическое занятие №2
Расчет электрических цепей с использованием законов Ома и Кирхгофа

Вопросы для подготовки к занятиям

1. Сформулировать закон Ома для участка и для замкнутого контура.

2. Нарисовать схемы с последовательным и параллельным соединением пассивных элементов, указать основные свойства этих соединений, схему со смешанным соединением пассивных элементов; дать порядок расчета этих схем.

3. Нарисовать схемы соединения пассивных элементов звездой и треугольником и объяснить порядок их расчета.

4. Сформулировать первый и второй законы Кирхгофа, объяснить правила знаков.

5. Сформулировать уравнение баланса мощностей.

6. Как составляется система уравнений для расчета сложных схем при помощи уравнений Кирхгофа?

6.1.2. Расчет цепи с одним источником питания

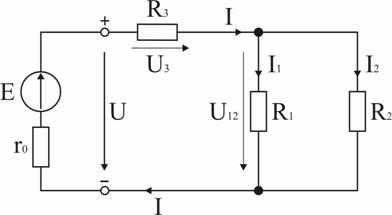
Задача 1. В цепи, схема которой приведена на рис. 1.29, ЭДС аккумуляторной батареи Е = 78 В, ее внутреннее сопротивление r₀ = 0,5 Ом. Сопротивления резисторов R₁ = 10 Ом, R₂ = 5 Ом, R₃ = 4 Ом. Вычислить токи во всех ветвях цепи и напряжения на зажимах батареи и на каждом их резисторов.

Анализ и решение задачи 1

1. Обозначение токов и напряжений на участках цепи.

Резистор R₃ включен последовательно с источником, поэтому ток I для них будет общим, токи в резисторах R₁ и R₂ обозначим соответственно I₁и I₂. Аналогично обозначим напряжения на участках цепи.

2. Определение эквивалентного сопротивления цепи:

R_э = r₀ + R₃ + R₁ R₂ / (R₁ + R₂) = 0,5 + 4 + 5 * 10 / (5 +10) = 7,8 Ом

3. Ток в цепи источника рассчитываем по закону Ома:

I = E / R_э = 78 / 7,8 = 10 А.

4. Определение напряжений на участках цепи:

U₁₂ = R₁₂ I = 3,3 * 10 = 33 В; U₃ = R₃ I = 4 * 10 = 40 В;

U = E - r₀ I = 78 - 0,5 * 10 = 73 В.

5. Определение токов и мощностей всех участков:

I₁ = U₁₂ / R₁ = 33 / 10 = 3,3 А; I₂ = U₁₂ / R₂ = 33 / 5 = 6,6 А;

P₁ = R₁ I₁² = U₁₂ I₁ = 108,9 Вт; P₂ = R₂ I₂² = U₁₂ I₂ = 217,8 Вт;

P₃ = R₃ I² = U₃ I = 400 Вт.

Мощность потерь на внутреннем сопротивлении источника

P = r₀ I² = 50 Вт.

Мощность источника P = E I = 780 Вт.

Дополнительные вопросы к задаче 1

1. Как проверить правильность решения задачи?

Правильность вычисления токов можно проверить, составив уравнение на основании первого закона Кирхгофа: I = I₁ + I₂.

Правильность расчета мощностей проверяют по уравнению баланса мощностей: P = P₁ + P₂ + P₃ + P.

2. Каким будет напряжение на зажимах источника, при обрыве в цепи резистора R₃?

Это будет режим холостого хода источника ЭДС, при котором U = E, т.к. ток I равен 0 и I r₀ = 0.

3. Каким будет ток в цепи источника при коротком замыкании на его зажимах?

В режиме короткого замыкания U = 0 и ток источника ограничивается только его внутренним сопротивлением

I_кз = E / r₀ = 78 / 0,5 = 156 А.

4. Как изменятся токи в схеме при увеличении R₁?

При увеличении R₁ увеличивается сопротивление параллельного участка схемы R₁₂, поэтому увеличивается сопротивление R_экв, что приводит к уменьшению тока I. При уменьшении I уменьшаются падения напряжения I R₃ и I r₀ и, в соответствии со вторым законом Кирхгофа, напряжение на разветвлении U₁₂ = E - I (R₃ + r₀) возрастает, что приводит к увеличению тока в резисторе R₂. Т.к. ток I уменьшается, а ток I₂ возрастает, ток I₁ = I - I₂уменьшается.

Расчет сложных цепей при помощи уравнений Кирхгофа

Задача 2. Рассчитать схему рис. 1.30, составив систему уравнений на основании законов Кирхгофа.

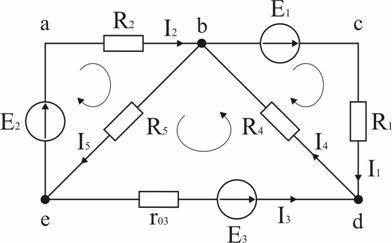
Исходные данные к задаче:

E₁ = 60 В; E₂ = 80 В; E₃ = 70 В;

R₁ = 20 Ом; R₂ = 50 Ом; r₀₃ = 5 Ом; R₄ = 65 Ом; R₅ = 85 Ом.

Анализ и решение задачи 2

1. Определение необходимого числа уравнений.

В схеме рис. 1.30 пять ветвей и для расчета токов в них надо составить пять уравнений. По первому закону Кирхгофа составляются уравнения для всех узлов, кроме одного (уравнение для него будет следствием предыдущих), по второму – для независимых контуров (в каждый последующий контур входит хотя бы одна ветвь, не вошедшая в ранее рассмотренные). Для данной схемы надо составить два уравнения по первому закону и три – по второму.

2. Составление и решение системы уравнений.

Для составления уравнений задаемся произвольно направлениями токов в ветвях и направлениями обхода контуров (рис. 1.30).

Уравнение для узла d: I₁ + I₃ - I₄ = 0.
Уравнение для узла е: - I₂ - I₃ + I₅ = 0.
Уравнение для контура bcd: I₁R₁ + I₄R₄ = E₁.
Уравнение для контура abe: I₂R₂ + I₅R₅ = E₂.
Уравнение для контура bde: I₃r₀₃ + I₄ R₄ + I₅R₅ = E₃.

Подставив в уравнения численные значения величин, получим алгебраическую систему уравнений:

I₁ + I₃ - I₄ = 0;
- I₂ - I₃ + I₅ = 0;
20 I₁ + 65 I₄ = 60;
50 I₂ + 85 I₅ = 80;
5 I₃ + 65 I₄ + 85 I₅ = 70.

Решение системы дает значения токов: I₁ = 1,093 А; I₂ = 0,911 А; I₃ =  –0,506 А; I₄ = 0,587 А; I₅ = 0,405 А.

Дополнительные вопросы к задаче 2

1. Что означает минус перед численным значением тока I₃?

Знак «–» говорит о том, что реальное направление тока в данной ветви противоположно принятому в начале расчета.

2. В каких режимах работают элементы схемы, содержащие источники ЭДС?

В ветвях с E₁ и E₂ токи совпадают по направлению с ЭДС, т.е. данные элементы работают источниками, отдавая энергию в схему; в ветви с ЭДС E₃ ток направлен против ЭДС, т.е. данный элемент работает потребителем (например, машина постоянного тока в режиме двигателя).

3. Как проверить правильность решения задачи?

Для проверки правильности расчета можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы. Независимой проверкой является уравнение баланса мощностей: сумма мощностей источников равна сумме мощностей, расходуемых в резистивных элементах схемы. Т.к. элемент схемы с ЭДС может работать как в режиме источника, так и в режиме потребителя, соответствующее слагаемое в левой части уравнения берется с плюсом, если Е и I совпадают по направлению (источник), и с минусом, если направления противоположны (потребитель).

Мощности элементов схемы с ЭДС:

E₁I₁+ E₂I₂ - E₃I₃ = 60 * 1 * 1,093 + 80 * 0,911 - 70 * 0,506 = 104,04 Вт.

Мощности, расходуемые в резистивных элементах схемы:

I₁²R₁ + I₂²R₂ + I₃²r₀₃ + I₄²R₄+ I₅²R₅ = 1,093² * 20 + 0,911² * 50 + 0,506² * 5 + 0,587² * 65 + 0,405² * 85 = 103,01 Вт

EI = P Баланс мощностей сошелся, следовательно задача решена верно.

Практическое занятие №3.
Методы расчета сложных цепей

Вопросы для подготовки к занятиям

1. Назовите основные режимы работы электрических цепей и укажите на их особенности.

2. Поясните, что такое активный и пассивный двухполюсники?

3. В каком случае источники питания можно представить в виде «источника ЭДС» или «источника тока» ?

4. Чем объясняется наклон внешних характеристик источников ЭДС и тока при работе под нагрузкой?

5. В каком случае целесообразно использовать для расчета метод узлового напряжения и в чем его особенности?

6. Что такое «метод эквивалентного генератора»?

7. Как определить параметры эквивалентного генератора (активного двухполюсника) расчетным и экспериментальным путем?

6.2.2. Расчет цепи методом узлового напряжения

Задача 1. В схеме рис. 1.31 E₁ = 60 В, E₂ = 48 В, E₃ = 6 В, R₁ = 200 Ом, R₂ = 100 Ом, r₀₃ = 0,5 Ом, R₃ = 9,5 Ом. Определить токи в ветвях схемы.

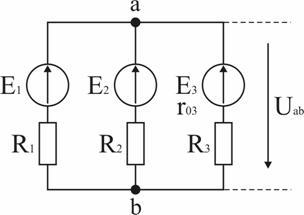
Анализ и решение задачи 1

1. Вычисление узлового напряжения. Для схемы с двумя узлами напряжение между ними можно подсчитать по формуле

,

где Е_i – ЭДС i-й ветви, g_i – ее проводимость  .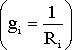

Подставляем числовые значения:

В.

2. Расчет токов в ветвях

Токи определяем на основании закона Ома для ветви с источником: напряжение на зажимах источника равно его ЭДС минус падение напряжения на его внутреннем сопротивлении:

А;

А;

А.

Дополнительные вопросы к задаче 1

1. Как повлияет на порядок расчета изменение полярности ЭДС в одной из ветвей схемы?

В формуле узлового напряжения и при расчете тока в этой ветви данную ЭДС надо брать со знаком «минус».

2. В каких режимах работают источники схемы?

По результатам расчета U_ab 1, U_ab 2, т.е. эти элементы схемы работают источниками; т.к. U_ab  E₃, т.к. в третьей ветви направлен против E₃ и принятого перед началом расчета направления I₃, т.е. этот элемент схемы работает в режиме потребления энергии.

3. В каких режимах будут работать источники, если за счет изменения величины ЭДС E₃ увеличить узловое напряжение U_ab до 48 В?

Увеличением E₃ можно установить U_ab = 48 В = E₂, при этом ток I₂ будет равен нулю (режим холостого хода), источник E₁ вырабатывает энергию, E₃ – потребляет. Ток в схеме и необходимую величину E₃ определим на основании второго закона Кирхгофа:

А;

E₃ = U_ab + I₃ (r₀₃ + R₃) = 48 - 0,06 * 10 = 47,4 В.

Расчет цепей методом эквивалентного генератора

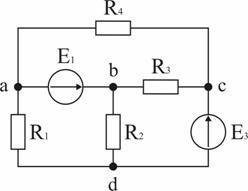
Задача 2. В схеме рис. 1.32 E₁ = 10 В, E₂ = 25 В, R₁ = 20 Ом, R₂ = 40 Ом, R₃ = 5 Ом, R₄ = 6,36 Ом. Определить ток в ветви с резистором R₄.

Анализ и решение задачи 2

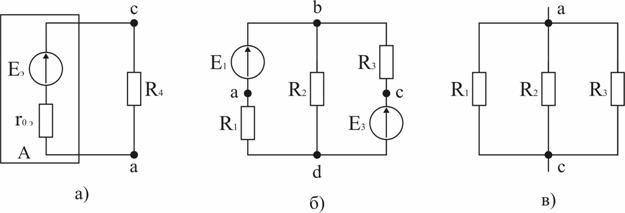
1. Заменим по отношению к ветви с резистором R₄ всю остальную схему эквивалентным генератором (активным двухполюсником) с ЭДС E_э и внутренним сопротивлением r_0э (рис. 1.33, а). ЭДС E_э определяется по результатам расчета режима холостого хода генератора как напряжение между точками «а» и «с» схемы рис. 1.32 при разомкнутой ветви с резистором R₄.

После размыкания ветви с R₄ получается схема с двумя узлами рис. 1.33, б. Узловое напряжение

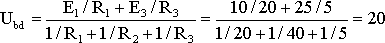В.

Ток в ветви с ЭДС E₃

I₃ = (E₃ - U_bd) / R₃ = (25 -20) / 5 = 1 А.

Для расчета напряжения между точками «а» и «с» в схеме рис. 1.33, б примем потенциал точки «а» равным нулю, тогда

_a = 0;  _b = _a + E₁ = 10 В; _c = _b + I₃R₃ = 15 В; E_r = _c -  _a = 15 В.

2. Для расчета внутреннего сопротивления генератора в схеме рис. 1.33, б закорачиваются все ЭДС (рис. 1.33, в) и определяется сопротивление по отношению к точкам «а» и «с»:

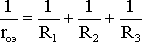; r_оэ = 3,64 Ом

3. Ток в ветви с резистором R₄ (схема рис. 1.33, а)

I₄ = E_э / (r_0э + R₄) = 20 / (3,64 + 6,36) = 2 А.

Дополнительные вопросы к задаче 2

1. Как экспериментально определить параметры эквивалентного генератора?

Исходя из эквивалентности схем рис. 1.32, а и рис. 1.33, а, E_э и r_0э можно рассчитать по результатам двух опытов. Разомкнув ветвь с R₄, измеряем напряжение между точками «с» и «а» U_xx, равное ЭДС E_э, (опыт холостого хода). Для определения r_0э проводится (если это допустимо) опыт короткого замыкания: заданная ветвь замыкается накоротко и измеряется ток в ней (I_к). При этом r_0э = E_э / I_к.

2. Выбрать величину сопротивления резистора R₄ так, чтобы в нем выделялась максимально возможная мощность.

Для схемы рис. 1.33, а 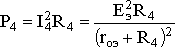 . Максимум мощности Р4 определяется решением уравнения  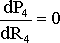: R_{н.экстр} = r_0э, при этом  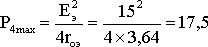Вт. Режим, когда сопротивление нагрузки равно внутреннему сопротивлению источника, называется согласованным, он часто используется в маломощных электронных устройствах, когда КПД установки ( 50 %) не имеет существенного значения, но важно передать в нагрузку максимальную мощность (усилители напряжения, маломощные усилители мощности, линии связи и т.д.). При этом все устройство по отношению к нагрузке представляется в виде эквивалентного генератора, параметры которого определяются по результатам анализа работы и расчета устройства.

Практическое занятие №4
Самостоятельная работа студента

В процессе выполнения самостоятельной работы студент должен решить нижеприведенные задачи, используя результаты первого и второго практических занятий. Отчет о проделанной работе должен быть представлен преподавателю по форме, указанной в методических указаниях. В отчете привести ответы на вопросы, приведенные в первом и втором практических занятиях и решения нижеприведенных задач.

 

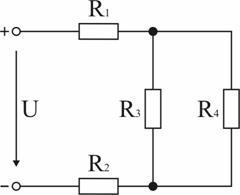
Задача 1. В схеме (рис. 1.34) R₁ = R₃ = 40 Ом, R₂ = 20 Ом, R₄ = 30 Ом, I₃ = 5 А. Вычислить напряжение источника U и ток I₄. Ответ: 900 В; 6,67 А.

Задача 2. В схеме (рис. 1.34) напряжение U = 65 В, напряжение на зажимах резистора R₄ равно 20 В. Определить все токи в схеме, если R₂ = 15 Ом, R₃ = 10 Ом, R₄ = 30 Ом. Ответ: I₁ = I₂ = 2 А; I₃ = 1,5 А; I₄ = 0,5 А.

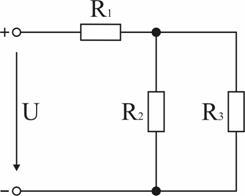
Задача 3. В схеме (рис. 1.35) – R₁ = 10 Ом, R₂ = 5 Ом, R₃ = 10 Ом, I₃ = 2 А. Найти напряжение источника U. Ответ: 80 В.

Задача 4. К схеме (рис. 1.35) приложено напряжение U = 45 В, при этом ток источника I₁ = 1,25 А. Сопротивления ветвей параллельной части схемы равны: R₂ = 40 Ом, R₃ = 10 Ом. Найти R₁ и токи I₂, I₃. Ответ: R₁ = 28 Ом, I₂ = 0,25 А, I₃=1 А.

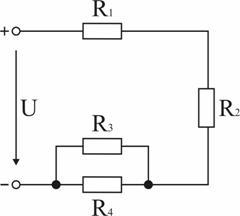
Задача 5. В схеме (рис. 1.36) – R₁ = 50 Ом, ток источника I = 0,6 А, ток в резисторе R₃ равен I₃ = 0,4 А, мощность, расходуемая в резисторе R₄: P₄ = 0,4 Вт; напряжение на резисторе R₂: U₂ = 36 В. Определить напряжение источника U. Ответ: U = 68 В.

Задача 6. Мощности, расходуемые в сопротивлениях схемы (рис. 1.36): P₁ = 15 Вт, P₂ = 20 Вт, P₃ = 10,8 Вт, P₄ = 7,2 Вт. Определить напряжения на участках схемы и токи в ее ветвях, если приложенное к ней напряжение U = 106 Вт. Ответ: I = 0,5 А; I₃ = 0,3 А; I₄ = 0,2 А; U₁ = 30 В; U₂ = 40 В; U = 36 В.

 

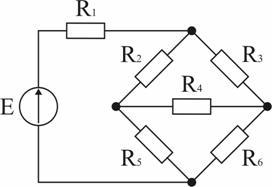
Задача 7. Для схемы (рис. 1.37) дано: R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 10 Ом, R₄ = 60 Ом, R₅ = 22 Ом, R₆ = 5 Ом, E = 12 В. Вычислить ток в диагонали моста R₄, используя преобразование треугольника резисторов R₂, R₃, R₄ в эквивалентную звезду. Ответ: I₄ = 0,077 А.

Задача 8. В схеме (рис. 1.37) определить ток источника, используя преобразование звезды резисторов R₂, R₄, R₅ в эквивалентный треугольник, если R₂ = 6 Ом, R₃ = 42 Ом, R₄ = 12 Ом, R₅ = 24 Ом, R₆ = 28 Ом, I₃ = 0,5 А. Ответ: I =  2,75 А.

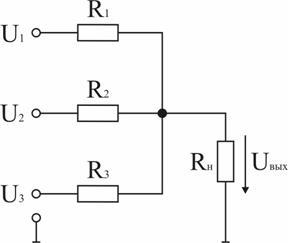
Задача 9. Для схемы (рис. 1.38) входные напряжения: U₁ = +10 В, U₂ = -15 В, U₃ = +20 В, R₁ = R₂ = R₃ = 500 Ом, R_н = 1000 Ом. Методом узлового напряжения определить выходное напряжение U_вых. Ответ: U_вых = 4,3 В.

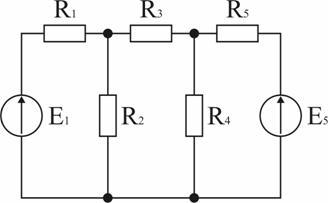
Задача 10. В схеме (рис. 1.39) E₁ = 120 В, E₅ = 140 В, R₁ = 70 Ом, R₂ = 30 Ом, R₃ = 135 Ом, R₄ = 210 Ом, R₅ = 140 Ом. Определить методом эквивалентного генератора величину и направление тока в резисторе R₃. Ответ: I₃ = 0,2 А.