МБОУ «СОШ с.Дачу-Борзой»
УРОК ПО ТЕМЕ:
«ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ»
10 КЛАСС
Составитель:
учитель математики
МБОУ «СОШ с.Дачу-
Борзой »
Бакашева Малика В.
2017 – 2018 уч. год
Проверила 20.11.2017г.
Завуч по УВР
Байбетирова З.В._________
Тема урока: «Показательные уравнения»
Учебник: Колягин Ю. М. Алгебра и начала математического анализа. 10 класс. Москва, «Просвещение», 2014.
Урок проведён в универсальном 10-м классе средней общеобразовательной школы.
Цели урока: изучение способов решения показательных уравнений, тренировка в применении полученных знаний при решении заданий по теме, развивать творческую и мыслительную деятельность учащихся, формировать умения чётко и ясно излагать свои мысли, формировать познавательные интересы и мотивы самосовершенствования, воспитывать умение работать с имеющейся информацией и культуру труда.
Структура урока.
Организационный этап. Постановка темы и цели урока.
- Прочитайте тему сегодняшнего урока.
- « Показательные уравнения».
- Нам это уже известно или это новый вид уравнений?
- Это новый вид уравнений.
- Попробуйте сформулировать цели урока.
- Мы узнаем, какие уравнения называются показательными, изучим способы их решения и будем учиться применять новое знание при решении задач по теме.
Учитель корректирует ответы учащихся.
Актуализация знаний. Устная работа.
Подберите корень уравнения 2х = 32; 3х = 27; 10х = 10000
Решите уравнение х2 = 36; х2 + х = 0; х2 + 2х + 1 = 0
Найдите область значений функции у = πх; у = (0,5)х; у = (0,5)|х|
Сравните, используя свойства функций, с единицей 2- 5; (0,5)- 3; (0,5)0,5
Изучение новогоматериала (лекция).
Уравнение, в котором неизвестное содержится в показателе степени, считается показательным. Рассмотрим основные виды показательных уравнений.
Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида ах = ав, где а 0, а ≠ 1. При этом используется свойство степени, которое мы изучали (повторить следствие 2 на стр. 160 учебника). Рассмотрим примеры решения таких уравнений(Можно заранее подготовить на слайдах).
Пример 1. ( 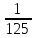 )0,2 х + 1 = 25;
)0,2 х + 1 = 25;
5 – 3 (0,2 х + 1) = 52;
- 0,6 х – 3 = 2;
- 0,6 х = 5;
х = - 8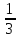 .
.
Ответ:- 8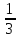 .
.
Пример 2. 36 · 6х = 1;
62 + х = 60;
2 + х = 0;
х = - 2.
Ответ: - 2.
Пример 3. 27х · 23х = 36;
32х · 23х = 62;
63х = 62;
3х = 2;
х = 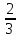 .
.
Ответ: 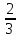 .
.
Пример 4. 2х – 3 = 3х – 3;
х – 3 = 0;
х == 3.
Ответ: 3.
Вынесение общего множителя за скобки.Рассмотрим примеры решения таких уравнений (Можно заранее подготовить на слайдах).
Пример 1. 2 · 3х + 1 – 6 · 3х – 1 – 3х = 9;
3х(2 · 3 – 6 · 3- 1 – 1) = 9;
3х · 3 = 9;
3х = 3;
х = 3.
Ответ: 3.
Пример 2. 52х – 7х - 52х · 17 + 7х · 17 = 0;
52х - 52х · 17 = 7х - 7х · 17;
52х(1 – 17) = 7х(1 – 17);
- 16· 52х = - 16 · 7х;
52х = 7х;
25х = 7х;
х= 0.
Ответ: 0.
Сведение к квадратному уравнению.Рассмотрим примеры решения таких уравнений (Можно заранее подготовить на слайдах).
Пример. 3 · 81х – 8 · 9х = 3;
3 · 81х – 8 · 9х – 3 = 0;
Замена 9х = t, t 0;
3 t2 - 8t – 3 = 0;
D = 64 +36 = 100;
t 1 = 3,
t2 = - 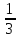 – не удовлетворяет условию t 0;
– не удовлетворяет условию t 0;
9х = 3;
32х = 3;
2х = 1;
х= 0,5.
Ответ: 0,5.
Закрепление изученного материала.
- Продолжаем учиться решать показательные уравнения. (Решение всех последующих уравнений записывается на доске с объяснениями, следует вызвать ученика по желанию). Разберём №680(2), 681(1), 682(3), 684(1), 693(2).
№680(2)
400х = 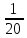 ;
;
202х = 20- 1;
2х = - 1;
х = - 0,5.
Ответ: - 0,5.
№681(1)
3 · 9х = 81;
31 + 2х = 34;
1 + 2х = 4;
х = 1,5.
Ответ: 0,5.
№682(3)
2х + 1 + 2х – 1 + 2х = 28;
2х(2 + 2- 1 + 1) = 28;
2х · 3,5 = 28;
2х = 8;
х = 3.
Ответ: 3.
№684(1)
9х – 4 · 3х + 3 = 0;
32х – 4 · 3х + 3 = 0;
Замена 3х = t, t 0;
t2 - 4t + 3 = 0;
D = 16 - 12 = 4;
t 1 = 3, t2 = 1;
3х = 3; х = 1;
3х = 1; 3х = 30; х = 0;
Ответ: 1; 0.
№693(2)
3х + 4 + 5х + 3 · 3 = 5х + 4 + 3х + 3;
3х + 4 - 3х + 3 = 5х + 4 - 5х + 3 · 3;
3х(34 – 33) = 5х(54 - 53 · 3);
3х · 54 = 5х · 250;
(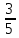 )х =
)х = 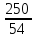 ;
;
(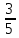 )х =
)х = 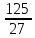 ;
;
(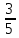 )х =(
)х =(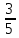 )- 3;
)- 3;
х = - 3.
Ответ: - 3.
Подведение итога урока. Рефлексия.
- Итак, подведём итоги проделанной работы. Что нового вы узнали?
- С какими видами показательных уравнений мы познакомились?
Домашнее задание.
Стр. 226 – 228, № 679, № 684(3), № 690(1).





