Урок математики в 5 классе
в технологии деятельностного метода
«Сложение и вычитание дробей
с разными знаменателями»
(урок открытия новых знаний).
Технологическая карта к уроку.
Урок математики в 5 классе ФГОС ООО
Тема урока: «Сложение и вычитание дробей с разными знаменателями».
Тип урока: урок открытия новых знаний
Класс: 5
Автор УМК: Линия учебно-методических комплексов «СФЕРЫ». Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений/ Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова и др., «Просвещение» 2013 г.
Цели по содержанию:
Обучающие: формировать навыки сложения и вычитания дробей с разными знаменателями, тренировать способность к его практическому использованию
развивающие: развитие умения анализировать, сравнивать, обобщать, проводить аналогию, делать выводы, развивать внимание.
воспитывающие: воспитание культуры устной и письменной речи, внимательности, аккуратности, культуры общения, воспитание профессионального интереса.
Планируемые результаты учебного занятия:
Предметные: построить алгоритм сложения и вычитания дробей с разными знаменателями, тренировать способность к его практическому применению, объяснять содержательный смысл сложения и вычитания дробей с разными знаменателями.
Метапредметные:
регулятивные: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения
коммуникативные: воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
познавательные: формировать навыки сложения и вычитания дробей с разными знаменателями; научить правильно, читать и записывать выражения, содержащие обыкновенные дроби;
Личностные: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний
Используемая технология: технология деятельностного метода
Демонстрационный материал:
Слайд 2. Медальный зачет. XXII олимпийские зимние игры в Сочи.




Слайд 3. Фотографии паралимпийцев.






Плакат на стене.
«Без знания дробей никто не может признаваться знающим математику». Цицерон.
Слайд 4-10 (Устная работа).
правило сложения и вычитания дробей с одинаковыми знаменателями в общем виде:


алгоритм сложения и вычитания дробей с одинаковыми знаменателями:
Алгоритм сложения и вычитания дробей с одинаковыми знаменателями Чтобы сложить или вычесть дроби с одинаковыми знаменателями нужно: Знаменатель оставить без изменения. Сложить (или вычесть) числители. Если в результате получилась дробь: сократимая, то ее обязательно сократить; неправильная, то из нее обязательно выделить целую и дробную части.
алгоритм сложения и вычитания дробей с разными знаменателями:
Алгоритм сложения и вычитания дробей с разными знаменателями Чтобы сложить или вычесть дроби с разными знаменателями нужно: Найти дополнительные множители для каждой дроби, разделив для этого наименьший общий знаменатель на знаменатель каждой дроби. Умножить числитель и знаменатель каждой дроби на её дополнительный множитель, записать сумму (разность) получившихся дробей. Знаменатель оставить без изменения. Сложить (или вычесть) числители. Если в результате получилась дробь: 1) сократимая, то ее обязательно сократить; 2) неправильная, то из нее обязательно выделить целую и дробную части.
Найти наименьший общий знаменатель дробей (найти наименьшее общее кратное знаменателей этих дробей).
образец выполнения задания в парах:
Образец

плакат (пьедестал с I,II, III местами)

Раздаточный материал:
Карточка с задание №1
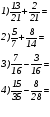
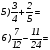
самостоятельная работа для работы в парах:
Карточка №2

самостоятельная работа с самопроверкой по эталону:
Вариант 2 Вариант 1






Карточка №3 (включение в систему знаний и повторение)



эталон для самопроверки:
Вариант 1
1) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (3; 4) = 12 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу сумму получившихся дробей. Применяю алгоритм сложения дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители складываю. Получилась неправильная дробь. Выделяю целую часть. 2) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (5; 10) = 10 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу разность получившихся дробей. Применяю алгоритм вычитания дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители вычитаю. Получилась сократимая дробь. Сокращаю дробь.










Эталон для самопроверки:
Вариант 1
3) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (9; 6) = 18 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу сумму получившихся дробей. Применяю алгоритм сложения дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители складываю.




Эталон для самопроверки:
Вариант 2
1) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (5; 7) = 35 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу сумму получившихся дробей. Применяю алгоритм сложения дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители складываю. Получилась неправильная дробь. Выделяю целую часть. 2) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (9; 18) = 18 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу разность получившихся дробей. Применяю алгоритм вычитания дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители вычитаю. Получилась сократимая дробь. Сокращаю дробь.









Эталон для самопроверки:
Вариант 2
3) Приведу дроби к наименьшему общему знаменателю, для этого найду наименьшее общее кратное знаменателей этих дробей. НОК (6; 8) = 24 Найду дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель разделю на знаменатель каждой дроби и запишу дополнительные множители над каждой дробью. Числитель и знаменатель каждой дроби умножу на ее дополнительные множители, запишу сумму получившихся дробей. Применяю алгоритм сложения дробей с одинаковыми знаменателями, знаменатель оставляю без изменения, числители складываю.
Ход урока:
1. Мотивация к учебной деятельности.
- Здравствуйте, дети! Я рада приветствовать вас на уроке математики.
- Скажите, вам нравится добиваться побед?
- А что для этого необходимо? (Дети перечисляют: сила воли, упорство, смекалка; нужно трудиться; учение и труд все перетрут.)
- Многократные тренировки, трудолюбие, воля, настойчивость, желание победить, вера в свои силы позволило нашим спортсменам занять первое место среди стран участниц в 22-х олимпийских зимних играх в Сочи. И мы ими гордимся.
- Посмотрите на экран. (Слайд 2. Медальный зачет. XXII олимпийские зимние игры в Сочи.)
Итак, каково общее количество медалей, завоеванных Россией? (33 медали)
- Сколько золотых? (13 медалей)
- Сколько серебряных? (11 медалей)
- Сколько бронзовых? (9 медалей)
- А какую серьезную тему мы изучаем? (Мы изучаем тему «Обыкновенные дроби».)
- Какую часть всех медалей составляют золотые медали?
- Что можете сказать о данной дроби? (Правильная, несократимая.)
- Какую часть всех медалей составляют серебряные медали? Верно ли, что серебряные медали составляют треть всех медалей? Почему? Какая это дробь? (Правильная, сократимая)
- А какая еще проходила олимпиада? (Паралимпийские игры 2014.)
- Что означает паралимпиада? (Международные спортивные соревнования для людей с ограниченными возможностями.)
- У этих спортсменов огромная сила воли, огромное мужество, что позволяет сборной России в медальном зачете уверенно лидировать. (Слайд 3. Фотографии паралимпийцев.)
|
|
- Сегодня в копилке общекомандного медального зачета российских паралимпийцев 80 медалей. Из них 30 золотых, 28 серебряных, 22 бронзовых.
Плакат на стене.
- Марк Туллий Цицерон - древнеримский политик и философ, блестящий оратор однажды сказал:
«Без знания дробей никто не может признаваться знающим математику». Цицерон.
- Сегодня на уроке вы покажите, какие еще знания уже имеете по теме «Обыкновенные дроби».
- И надеюсь благодаря трудолюбию, смекалке, умению применять полученные знания в новой ситуации, позволит вам самостоятельно открыть новые знания.
2. Актуализация знаний и фиксация затруднения в пробном действии.
- А начнём мы как всегда с устной работы, потому, что чтобы узнать что-то новое необходимо повторить уже изученный материал.
1) Актуализация знаний о сокращении дробей, выделении целой части из неправильной дроби, приведении дробей к наименьшему общему знаменателю, сравнении дробей с разными знаменателями.
Устная работа: Слайды 4-10 (Вспоминают и выполняют задания.)
Верно, ли выполнено задание?
Приведите дроби к наименьшему общему знаменателю.
и
Найдите ошибку:
Сравните дроби:
; б)
; в)
г) и
ч.
4. Назовите наименьший общий знаменатель дробей:
Выдели целую часть из неправильной дроби
- Молодцы! Вы хорошо поработали устно. Теоретические знания нам очень будут необходимы.
2) Актуализация знаний алгоритма сложения и вычитания дробей с одинаковыми знаменателями.
- Какие еще операции с дробями вы умеете выполнять? (Складывать и вычитать дроби с одинаковыми знаменателями.)
- Найдите сумму и разность дробей в первых четырех заданиях на карточке №1.
Если потребуется, сократите и выделите целую часть.
Первые два задания выполняет один ученик с комментарием у доски, два следующих задания выполняет другой, остальные учащиеся работают в тетрадях.
- А каким правилом сложения и вычитания дробей вы воспользовались? Запишите его в общем виде для дробей . Т.е. алгоритмом сложения и вычитания. (Дети, обсудив в парах, записывают в тетради.)
- Проверьте себя. Карточка с правилом в общем виде вывешивается на доску.
| |
- Давайте восстановим алгоритм сложения и вычитания дробей с одинаковыми знаменателями: (дети проговаривают алгоритм)
Алгоритм на слайде № 11.
- Хорошо.
- Предлагаю выполнить 5) и 6) задание на карточке №1.
Карточка с задание №1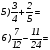 ?
?
- Чем отличается предыдущее задание, с которым вы все хорошо справились от этого? Что нового? (В предыдущих заданиях дроби были с одинаковыми знаменателями. А в последних заданиях у дробей разные знаменатели.)
- Чему будет посвящен урок?
- Найдите сумму и разность дробей.
Учащиеся выполняют решение в тетрадях. Два ученика за доской.
- Проверим результаты.
- У кого нет результата?
- Что вы не смогли сделать?
- Назовите, какие результаты получили.
Дети называют получившиеся результаты. Если среди них есть неправильные результаты, то учитель указывает на это.
- Что вы не смогли сделать? (Мы не смогли правильно выполнить задание.)
- Каким правилом пользовались те, кто получил правильный ответ? (Мы не можем указать правило.)
3. Выявление места и причины затруднения.
- Почему у вас получились такие разные ответы? Как выяснить? - Что необходимо сделать? (Остановиться и подумать, почему получились такие результаты.)
- Какое задание выполняли? (Складывали и вычитали дроби с разными знаменателями.)
- Как пробовали выполнять задание? (…)
- Где возникло затруднение? (В оформлении решения и не хватило время.)
- Почему не смогли выполнить задание? (У нас нет способа нахождения суммы и разности дробей с разными знаменателями.)
4. Построение проекта выхода из затруднения.
Сформулируйте цель сегодняшнего урока. (Построить алгоритм сложения и вычитания дробей с разными знаменателями, научиться выполнять действия по построенному алгоритму.)
- Сформулируйте тему урока. (Сложение и вычитание дробей с разными знаменателями.)
Учитель открывает на слайде № 12 тему урока.
- Запишите тему урока.
- Каким, известным способом, можете найти значения выражений? (Алгоритм сложения и вычитания дробей с одинаковыми знаменателями.)
- Как вы будете действовать? (Используем алгоритм сложения и вычитания дробей с одинаковыми знаменателями, изменим алгоритм, сформулируем алгоритм сложения и вычитания дробей с разными знаменателями.)
5. Реализация построенного проекта.
Задание парам:
- Дополнить известный алгоритм сложения и вычитания дробей с одинаковыми знаменателями шагом или шагами, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателями.
Учащиеся работают в парах 5 минут, обсуждаются итоги работы пар. Учащиеся пытаются сформулировать алгоритм сложения и вычитания дробей с разными знаменателями. Учитель может организовать подводящий диалог.
- Вернемся к нашим выражениям и найдем их значения, используя полученный алгоритм.
- Будьте внимательны при оформлении задания!
Кто-то из детей проговаривает и записывает у доски (учитель помогает правильно оформить задание).
| 5)
|
- С чего начнете сложение дробей с разными знаменателями?
(Приведём дроби к наименьшему общему знаменателю, для этого найдём наименьшее общее кратное знаменателей этих дробей, т.е. 5 и 4.)
НОК (5; 4) = 20
(Затем найдем дополнительные множители для каждой дроби, для этого наименьший общий знаменатель разделим на знаменатель каждой дроби и запишем дополнительные множители над каждой дробью.)
Дополнительный множитель первой дроби 5, второй дроби 4.
(Затем числитель и знаменатель каждой дроби умножим на ее дополнительные множители, запишем сумму получившихся дробей.)
Запись дробей будет иметь вид:
;
(Применим алгоритм сложения дробей с одинаковыми знаменателями, знаменатель оставляем без изменения, числители складываем.)
- Какая дробь получилась? (Дробь неправильная.)
- Какой завершающий шаг? (Выделим из неё целую и дробную части.)
Получаем:
- Обратите внимание, при сложении дробей с разными знаменателями запись в тетради можно оформить так:
|
6)
|
Проводим аналогичные рассуждения.
- На слайде № 13 появляется алгоритм сложения и вычитания дробей с разными знаменателями.
- Сравните полученный алгоритм с правилом в учебнике на стр. 157. Обратите внимание на оформление решения в учебнике.
Дети читают правило про себя, затем один ученик вслух.
- Справились с затруднением? – Молодцы!
- Какие задания вы теперь можете выполнять? (Мы теперь можем складывать и вычитать дроби с разными знаменателями.)
6. Первичное закрепление с проговариванием во внешней речи.
- А теперь что необходимо в дальнейшей работе на уроке? (Тренировка.)
- Найдите значения выражений записанных на доске, проговаривая свои действия по алгоритму. (По одному ученику комментируют решение по алгоритму.)
Задания на доске.
Вычислите: Решение учащихся:
– Предлагаю теперь поработать в парах.
Найдите значения выражений на карточке №2, проговаривая друг другу действия по алгоритму.
Самостоятельная работа на закрепление
Карточка №2

Работа проверяется по образцу.
- Повторите еще раз алгоритм сложения и вычитания дробей с разными знаменателями.
7. Самоконтроль с самопроверкой по эталону.
- Выполните задание самостоятельно.
Дети выполняют задание, после чего учитель открывает на доске или раздаёт эталон для самопроверки.
- Проверьте работу по эталону.
- Кто действовал так же и получил тот же результат – поставьте «+». – Молодцы!
- У кого получился другой ответ – поставьте «!», найдите по шагам место, где допущена ошибка, обведите её. – Обратите внимание на это место. – Молодцы в том, что сумели найти место, в котором допущена ошибка. – Поставьте рядом «+».
Самостоятельная работа с самопроверкой по эталону:
Вариант 2 Вариант 1






8. Включение в систему знаний и повторение.
- Новое знание вам пригодится не только при решении примеров. Где ещё вы можете встретиться со сложением и вычитанием дробей с разными знаменателями? (При нахождении значения выражения, сравнении выражений, решении задач, уравнений…)
- Предлагаю вам применить свои новые знания при решении уравнений.
- Выберите то уравнение, при решении которого нужно будет использовать новое знание.
Учащимся даётся несколько минут, для того чтобы выбрать уравнение. Затем по одному ученику на закрытой части доски решают выбранное ими уравнение, остальные у себя в тетрадях.
Далее проводится обсуждение решённых уравнений и проверка. Дети, которые произвели правильный выбор и решение ставят в тетрадях «+», «+».
9. Рефлексия учебной деятельности на уроке.
- Что нового узнали на уроке?
- Были удачи на уроке? Какие? (Справились с затруднением, научились складывать и вычитать дроби с разными знаменателями.)
- Что нам помогло справиться с затруднением?
- Достигли цели урока? (..)
- Сегодня вы ещё на один шаг продвинулись в своём обучении.
- Как бы вы отметили работу всего класса? (Выслушиваются 1-2 ученика.)
- Оцените лично свою работу на уроке. (На доске изображён пьедестал с I,II, III местами).
- Дети, вы очень много работали на сегодняшнем уроке, и, несомненно, добились побед, больших и маленьких. Выходите к доске и прикрепите стикеры на пьедестал на уровни, которых, по вашему мнению, достигли на сегодняшнем уроке. Вперед, к новым победам!
- Как вы думаете, на следующем уроке пригодятся новые знания?
Далее учитель предлагает учащимся записать домашнее задание.
Постановка домашнего задания с комментарием.
Домашнее задание: Правило стр. 157 учебник, алгоритм учить (раздать каждому), У: № 546 (б, в,), № 547 (а, б), № 549(а, б), № 556
Технологическая карта урока
Предмет: Математика
Класс: 5
Автор УМК: Линия учебно-методических комплексов «СФЕРЫ». Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений/ Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова и др., «Просвещение» 2013 г.
Тема урока: «Сложение и вычитание дробей с разными знаменателями».
Тип урока: урок открытия новых знаний
Цель урока: Формировать навыки сложения и вычитания дробей с разными знаменателями.
Задачи урока:
Образовательные: формировать навыки сложения и вычитания дробей с разными знаменателями, тренировать способность к его практическому использованию
Развивающие: развитие умения анализировать, сравнивать, обобщать, проводить аналогию, делать выводы; развивать внимание, память, умение рассуждать и аргументировать свои действия через решение проблемной задачи.
Воспитывающие: воспитание культуры устной и письменной речи, внимательности, аккуратности, культуры общения, воспитание интереса к предмету.
Планируемые результаты учебного занятия:
Предметные: построить алгоритм сложения и вычитания дробей с разными знаменателями, тренировать способность к его практическому применению, объяснять содержательный смысл сложения и вычитания дробей с разными знаменателями.
Метапредметные:
Регулятивные: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения
Коммуникативные: воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления; участвовать в диалоге, в общей беседе, выполняя принятые правила речевого поведения; задавать вопросы, отвечать на вопросы других; под руководством учителя участвовать в организации и осуществлении парной работы: распределять роли, сотрудничать, оказывать взаимопомощь, взаимоконтроль, проявлять доброжелательное отношение к партнёрам.
Познавательные: формировать навыки сложения и вычитания дробей с разными знаменателями; научить правильно, читать и записывать выражения, содержащие обыкновенные дроби;
Личностные: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний
Используемая технология: технология деятельностного метода
Оснащение урока: ноутбук, проектор, экран, презентация к уроку; карточки для работы в парах.
| Этап урока | Деятельность учителя | Деятельность учащегося | |||||||||
|
|
| Познавательная | Коммуникативная | Регулятивная | Личностная | ||||||
|
| Осуществляемые действия
| Осуществляемые действия
| Формируемые способы деятельности
| Осуществляемые действия
| Формируемые способы деятельности
| Осуществляемые действия
| Формируемые способы деятельности
|
| |||
| 1.Мотивация к учебной деятельности.
| Организует мотивирование к учебной деятельности. Приветствует учащихся, проверяет их готовность к уроку. - Скажите, вам нравится добиваться побед? - А что для этого необходимо? (Дети перечисляют: сила воли, упорство, смекалка; нужно трудиться; учение и труд все перетрут.) - Многократные тренировки, трудолюбие, воля, настойчивость, желание победить, вера в свои силы позволило нашим спортсменам занять первое место среди стран участниц в 22-х олимпийских зимних играх в Сочи. И мы ими гордимся. - Посмотрите на экран. (Слайд 2. Медальный зачет. XXII олимпийские зимние игры в Сочи.) Итак, каково общее количество медалей, завоеванных Россией? (33 медали) - Сколько золотых? (13 медалей) - Сколько серебряных? (11 медалей) - Сколько бронзовых? (9 медалей) - А какую тему мы изучаем? (Мы изучаем тему «Обыкновенные дроби».) - Какую часть всех медалей составляют золотые медали? - Что можете сказать о данной дроби? (Правильная, несократимая.) - Какую часть всех медалей составляют серебряные медали? Верно ли, что серебряные медали составляют треть всех медалей? Почему? Какая это дробь? (Правильная, сократимая)
Плакат на стене. - Марк Туллий Цицерон - древнеримский политик и философ, блестящий оратор однажды сказал: «Без знания дробей никто не может признаваться знающим математику». /Цицерон./ - Сегодня на уроке вы покажите, какие еще знания уже имеете по теме «Обыкновенные дроби». - И надеюсь благодаря трудолюбию, смекалке, умению применять полученные знания в новой ситуации, позволит вам самостоятельно открыть новые знания. - А начнём мы как всегда с устной работы, потому, что чтобы узнать что-то новое необходимо повторить уже изученный материал. |
|
| Концентрируют внимание. Слушают, вступают в диалог. | Планирование учебного сотрудничества с учителем и одноклассниками. | Получают позитивный заряд. | Настраиваются на успешную деятельность | Готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию. Выражать положительное отношение к процессу познания, проявлять желание узнать новое. | |||
| 2.Актуализа-ция знаний и фиксация затруднения в пробном действии. | 1) Организует повторение теоретических знаний и практических навыков учащихся в процессе выполнения устных заданий по слайдам презентации. (Слайды 4-10) - Молодцы! Вы хорошо поработали устно. Теоретические знания нам очень будут необходимы. 2) Организует повторение алгоритма сложения и вычитания дробей с одинаковыми знаменателями. - Какие еще операции с дробями вы умеете выполнять? (Складывать и вычитать дроби с одинаковыми знаменателями.) Предлагает найти сумму и разность дробей в первых четырех заданиях на карточке №1 (выполняют по одному ученику с комментарием у доски, остальные учащиеся работают в тетрадях). - Если потребуется, сократите и выделите целую часть. - А каким правилом сложения и вычитания дробей вы воспользовались? Предлагает вспомнить алгоритм сложения и вычитания дробей с одинаковыми знаменателями и записать его в общем виде для дробей - Проверьте себя. Карточка с правилом в общем виде вывешивается на доску. - Давайте восстановим алгоритм сложения и вычитания дробей с одинаковыми знаменателями: (дети проговаривают алгоритм) Алгоритм на Слайде № 11. - Хорошо. 3) Мотивирует учащихся к пробному учебному действию, организует его самостоятельное выполнение и фиксацию индивидуальных затруднений. - Предлагаю выполнить 5) и 6) задание на карточке №1.
- Чем отличается предыдущее задание, с которым вы все хорошо справились от этого? Что нового? (В предыдущих заданиях дроби были с одинаковыми знаменателям, а в последних заданиях у дробей разные знаменатели.) - Чему будет посвящен урок? - Найдите сумму и разность дробей. Учащиеся выполняют решение в тетрадях. Два ученика за доской. - Проверим результаты. - У кого нет результата? - Что вы не смогли сделать? - Назовите, какие результаты получили. Дети называют получившиеся результаты. Если среди них есть неправильные результаты, то учитель указывает на это. - Что вы не смогли сделать? (Мы не смогли правильно выполнить задание.) - Каким правилом пользовались те, кто получил правильный ответ? (Мы не можем указать правило.) | Повторяют знания о сокращении дробей, выделении целой части из неправильной дроби, приведении дробей к наименьшему общему знаменателю, сравнении дробей с разными знаменателями. Обсудив в парах алгоритм сложения и вычитания дробей с одинаковыми знаменателями в общем виде для дробей , записывают в тетради.
| Анализируя и сравнивая предлагаемые задания, извлекают необходимую информацию для построения математического высказывания. Формулирование проблемы.
| Выполняют задания. Отвечают на поставленные вопросы. Оформляют свои мысли в письменной и устной форме. Проговаривают алгоритм в ходе совместного выполнения типовых заданий. Выполняя пробное действие выходят на необходимость формулирования правила сложения и вычитания дробей с разными знаменателями. | Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. | Работают по алгоритму сложения и вычитания дробей с одинаковыми знаменателями. Проверяют себя.
| Оценка, выделение и осознание учащимися того, что уже усвоено и того, что еще нужно усвоить. | Смыслообразование.
| |||
| 3. Выявление места и причины затруднения. | Организует выявление и фиксирование во внешней речи причины затруднения. - Почему у вас получились такие разные ответы? Как выяснить? - Что необходимо сделать? (Остановиться и подумать, почему получились такие результаты.) - Какое задание выполняли? (Складывали и вычитали дроби с разными знаменателями.) - Как пробовали выполнять задание? (…) - Где возникло затруднение? (В оформлении решения и не хватило время.) - Почему не смогли выполнить задание? (У нас нет способа нахождения суммы и разности дробей с разными знаменателями.) | Восстанавливают выполненные операции и фиксируют (вербально и знаково) место – шаг, операцию, где возникло затруднение; соотносят свои действия с используемым способом действий (алгоритмом, понятием и т.д.), и на этой основе выявляют и фиксируют во внешней речи причину затруднения – те конкретные знания, умения или способности, которых недостает для решения исходной задачи. | Анализ, синтез, сравнение, обобщение, аналогия; подведение под понятие; использование знаково-символических средств; постановка и формулирование проблемы. | Отвечают на поставленные вопросы, высказывают свое мнение. | Учет разных мнений, координирование в сотрудничестве разных позиций |
| Волевая саморегуляция | Учебно-познавательный интерес, смыслообразование, эмпатия | |||
| 4. Построение проекта выхода из затруднения. | Организует в коммуникативной форме построение учащимися проекта будущих учебных действий: 1. уточнение цели проекта; 3. определение средств; 4. построение плана достижения цели. Сформулируйте цель сегодняшнего урока. (Построить алгоритм сложения и вычитания дробей с разными знаменателями, научиться выполнять действия по построенному алгоритму.) - Сформулируйте тему урока. (Сложение и вычитание дробей с разными знаменателями.) Учитель открывает на слайде № 12 тему урока. - Запишите тему урока. - Каким, известным способом, можете найти значения выражений? (Алгоритм сложения и вычитания дробей с одинаковыми знаменателями.) - Как вы будете действовать? (Используем алгоритм сложения и вычитания дробей с одинаковыми знаменателями, изменим алгоритм, сформулируем алгоритм сложения и вычитания дробей с разными знаменателями.) | В коммуникативной форме обдумывают план будущих учебных действий. | Построение логической цепи рассуждений, использование знаково-символических средств, построение речевых высказываний, выбор наиболее эффективных способов решения задач, определение основной и второстепенной информации. | Отвечают на поставленные вопросы, сотрудничают в ходе построения проекта выхода из затруднения. | Планирование учебного сотрудничества, формулирование и аргументация своего мнения и позиции в коммуникации | Ставят цель, согласовывают тему урока, строят план достижения цели, определяют средства (алгоритм).
| Познавательная инициатива, | Самоопределение, нравственно-этическое оценивание усваиваемого содержания.
| |||
| 5. Реализация построенного проекта. | Побуждает учащихся к теоретическому объяснению фактов. Стимулирует активное участие всех детей в поисковой деятельности. Формулирует обобщенные вопросы. Задание парам: - Дополнить известный алгоритм сложения и вычитания дробей с одинаковыми знаменателями шагом или шагами, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателями. Учащиеся работают в парах 5 минут, обсуждаются итоги работы пар. Учащиеся пытаются сформулировать алгоритм сложения и вычитания дробей с разными знаменателями. Учитель может организовать подводящий диалог. - Вернемся к нашим выражениям и найдем их значения, используя полученный алгоритм.
- Будьте внимательны при оформлении задания! Сильный ученик проговаривает и записывает у доски (учитель помогает правильно оформить задание). Демонстрирует коллективно составленный алгоритм. - На слайде № 13 появляется алгоритм сложения и вычитания дробей с разными знаменателями. - Сравните полученный алгоритм с правилом в учебнике на стр. 157. Дети читают правило про себя, затем один ученик вслух. - Справились с затруднением? – Молодцы! - Какие задания вы теперь можете выполнять? (Мы теперь можем складывать и вычитать дроби с разными знаменателями.) | Обосновывают выбор общего решения или несогласия с мнением других. Составляют алгоритм. Делают выводы о полноте и правильности, сравнивая с правилом в учебнике. Вносят изменения в индивидуальные алгоритмы. | Анализ, синтез, сравнение, обобщение, аналогия; выдвижение гипотез и их обоснование; использование знаково-символических средств; самостоятельное создание алгоритма деятельности. | Обсуждают в парах варианты решения учебной задачи. Сообщают о результатах поисковой работы, отвечают на вопросы учеников других пар. Фиксируют на бумаге, доске свое «открытие» | Учет разных мнений, координирование в сотрудничестве разных позиций; формулирование и аргументация своего мнения и позиции в коммуникации; достижение договоренностей и согласование общего решения. | Оценивают правильность своих выводов, решений. Осуществляют самопроверку, самооценку полученных результатов.
| Познавательная инициатива; волевая саморегуляция . | Нравственно-этическое оценивание усваиваемого содержания; осознание ответственности за общее дело;
| |||
| 6. Первичное закрепление с проговарива-нием во внешней речи. | Организует фиксирование нового знания в речи и знаках. Предлагает задания на «новое» знание, побуждает учеников к определению и выбору видов работы по достижению целей урока, помогает комментировать учебные действия «ведущему» (сильному ученику), поддерживает интерес и познавательную активность учащихся. Создает условия для сотрудничества – работы в парах. Создание ситуации успеха для каждого. - А теперь что необходимо в дальнейшей работе на уроке? (Тренировка.) 1) - Найдите значения выражений записанных на доске, проговаривая свои действия по алгоритму. (По одному ученику комментируют решение по алгоритму.) Задания на доске. Вычислите:
2) – Предлагаю теперь поработать в парах. Найдите значения выражений на карточке №2, проговаривая друг другу действия по алгоритму. | Отрабатывают действия, соответствующие мыслительным операциям анализа, синтеза, сравнения, обобщения. Решают типовые задания на сложение и вычитание дробей с разными знаменателями (фронтально, а затем в парах), с проговариванием алгоритма решения вслух. Проверяют по образцу. | Использование общих приемов решения задач; | Оформляют свои мысли в письменной и устной форме. Слушают и понимают партнера. | Планирование учебного сотрудничества, управление поведением партнера, умение выражать свои мысли, использование критериев для обоснования своего суждения, достижение договоренностей и согласование общего решения | Работают по алгоритму. | Контроль, | Осознание ответственности за общее дело, освоение новых социальных ролей и правил | |||
| 7.Самоконт-роль с самопровер-кой по эталону. | Организует выполнение учащимися самостоятельной работы на новое знание (Карточка по вариантам), с последующей самопроверкой по эталону. Организует выявление места и причины затруднений, работу над ошибками. -Выполните задание самостоятельно. Дети выполняют задание, после чего учитель открывает на доске или раздаёт эталон для самопроверки. - Проверьте работу по эталону. - Кто действовал так же и получил тот же результат – поставьте «+». – Молодцы! - У кого получился другой ответ – поставьте «!», найдите по шагам место, где допущена ошибка, обведите её. – Обратите внимание на это место. – Молодцы в том, что сумели найти место, в котором допущена ошибка. – Поставьте рядом «+». | Самостоятельно выполняют задания нового типа и осуществляют их проверку, пошагово сравнивая с эталоном. Называют место своего затруднения, причину. Исправляют ошибки. | Анализ, сравнение, использование знаково-символических средств, использование общих приемов решения задач, рефлексия способов и условий действия. |
|
| Работают по алгоритму. | Работа по алгоритму; самостоятельный учет выделенных ориентиров действия в новом учебном материале; саморегуляция; осуществление самоконтроля по результату и по способу действия; | Развитие этических чувств и регуляторов морального поведения. | |||
| 8. Включение в систему знаний и повторение. | Организует выполнение задания, в которых новый способ действий предусматривается как промежуточный шаг. Создает условий для включения “открытия” в систему знаний, повторение и закрепление ранее изученного. - Новое знание вам пригодится не только при решении примеров. Где ещё вы можете встретиться со сложением и вычитанием дробей с разными знаменателями? (При нахождении значения выражения, сравнении выражений, решении задач, уравнений…) - Предлагаю вам применить свои новые знания при решении уравнений. - Выберите то уравнение, при решении которого нужно будет использовать новое знание. Карточка №3. | Выбирают уравнение. Затем по одному ученику на закрытой части доски решают выбранное ими уравнение, остальные у себя в тетрадях.
Отрабатывают сложение и вычитание дробей с разными знаменателями при решении уравнений; повторяют нахождение неизвестных компонентов уравнений. | Анализ, синтез, сравнение; | Проводят обсуждение решённых уравнений. | Формулирование и аргументация своего мнения и позиции в коммуникации; | Дети, которые произвели правильный выбор и решение ставят в тетрадях «+», «+».
| Прогнозирование. | Нравственно-этическое оценивание усваиваемого содержания. | |||
| 9. Рефлексия учебной деятельности на уроке. | Организует фиксирование нового содержания, рефлексию, самооценку учебной деятельности. Предлагает вспомнить тему урока и задачи урока, определить достигнуты ли цели урока и оценить меру своего личного продвижения к цели и успехи класса в целом. -Что нового узнали на уроке? - Были удачи на уроке? Какие? (Справились с затруднением, научились складывать и вычитать дроби с разными знаменателями.) - Что нам помогло справиться с затруднением? - Достигли цели урока? (..) - Сегодня вы ещё на один шаг продвинулись в своём обучении. - Как бы вы отметили работу всего класса? (Выслушиваются 1-2 ученика.) - Оцените лично свою работу на уроке. (На доске или слайде изображён пьедестал с I,II, III местами). - Дети, вы очень много работали на сегодняшнем уроке, и, несомненно, добились побед, больших и маленьких. Выходите к доске и прикрепите стикеры на пьедестал на уровни, которых, по вашему мнению, достигли на сегодняшнем уроке. Вперед, к новым победам! - Как вы думаете, на следующем уроке пригодятся новые знания? (…) | Определяют степень своего продвижения к цели. Отмечают успешные ответы, интересные вопросы одноклассников. | Умение структурировать знания, рефлексия способов и условий действия, оценка процесса и результатов деятельности | Называют тему и задачи урока, отмечают моменты, вызвавшие затруднение, наиболее понравившиеся эпизоды урока, высказывают оценочные суждения. | Формулирование и аргументация своего мнения, учет разных мнений, планирование учебного сотрудничества |
| Волевая саморегуляция, оценка – выделение и осознание того, что уже усвоено и что еще подлежит усвоению, прогнозирование. | Умение осуществлять самооценку на основе критерия успешности учебной деятельности, внутренняя позиция школьника, адекватное понимание причин успеха / неуспеха в учебной деятельности. | |||
| 10.Постанов-ка домашнего задания.
| Предлагает учащимся записать домашнее задание. Постановка домашнего задания с комментарием. Правило стр. 157 учебник, алгоритм учить (раздать каждому), У: № 546 (б, в,), № 547 (а, б), № 549(а, б), № 556 |
|
|
|
|
|
|
| |||
14