
Мастер класс «Удивительные люди».
Составила учитель математики Клопотова Наталья николаевна МОУСОШ №1 г.Буденновска

Цель мастер-класса:
показать использование устного приема счета в обучении математике через методические приемы.
Задачи мастер-класса:
• знакомство педагогов с приемами;
• создание условий для профессионального общения и стимулирование роста творческого потенциала педагогов;
• совместная отработка новых приемов.

1.прием: умножение двузначного числа на одиннадцать
Алгоритм вычисления:
1) Взять множитель, отличный от одиннадцати;
2) раздвинуть десятки от единиц;
3) найти сумму десятков и единиц;
4) записать эту сумму между десятками и единицами;
5) получаем ответ.
Рассмотрим пример: 45∙11
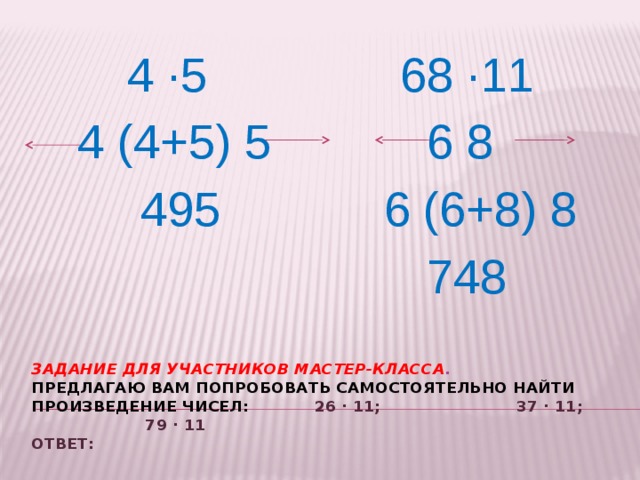
4 ∙5
68 ∙11
4 (4+5) 5
6 8
495
6 (6+8) 8
748
Задание для участников мастер-класса . Предлагаю Вам попробовать самостоятельно найти произведение чисел: 26 ∙ 11; 37 ∙ 11; 79 ∙ 11 Ответ:

2 прием: Нахождение квадрата числа, оканчивающегося пятеркой
Алгоритм вычисления:
1) умножаем первый десяток на второй десяток, но предварительно увеличив его на один;
2) записываем первое произведение;
3) умножаем единицы;
4) записываем второе произведение после первого произведения;
5) читаем ответ.

85∙85 =
35 ∙ 35=
8 ∙ 9=72
3 ∙ 4 =12
5 ∙ 5=25
5 ∙ 5=25
7225
1225
Задание для участников мастер-класса.
Предлагаю Вам попробовать самостоятельно найти произведение чисел:
65 ∙ 65; 95 ∙ 95

3 прием: умножение двух чисел, близких к ста. Алгоритм вычисления : Если умножаем двузначные числа, то ответ должен быть четырехзначным, если трехзначные числа, то ответ - шестизначный, и т. д. 1)представим каждый множитель в виде х= 100 - а; у=100 - в, где а - недостаток первого числа до сотни, а в - недостаток второго числа до сотни; 2) найти разность второго множителя и первого недостатка; 3) найти разность первого множителя и второго недостатка (причем оба ответа должны быть одинаковы); 4) записать результат первым; 5) найти произведение обоих недостатков и результат записать после первого результата; 6) читаем ответ Рассмотрим пример : 99*83 =

3 прием: умножение двух чисел, близких к ста.
Алгоритм вычисления:
Если умножаем двузначные числа, то ответ должен быть четырехзначным, если трехзначные числа, то ответ - шестизначный, и т. д.
1)представим каждый множитель в виде х= 100 - а; у=100 - в, где а - недостаток первого числа до сотни, а в - недостаток второго числа до сотни;
2) найти разность второго множителя и первого недостатка;
3) найти разность первого множителя и второго недостатка (причем оба ответа должны быть одинаковы);
4) записать результат первым;
5) найти произведение обоих недостатков и результат записать после первого результата;
6) читаем ответ
Рассмотрим пример :
99*83 =

Рассмотрим пример : 99 ∙ 83= 8217 (100 – 1) ∙ (100 – 17) 1)83-1=82 2)99-17=82 3)1 ∙ 17=17
Задание для участников мастер-класса.
Предлагаю Вам попробовать самостоятельно найти произведение чисел:
98 ∙ 86; 97 ∙ 94

4 прием: умножение двух чисел, близких к 10000.
Алгоритм вычисления:
Результат умножения будет восьмизначным числом, поставим 8 точек.
1)представим каждый множитель в виде х= 10000 - а; у=1000 0- в, где а - недостаток первого числа до десяти тысячи, а в - недостаток второго числа до десяти тысячи;
2) найти разность второго множителя и первого недостатка;
3) найти разность первого множителя и второго недостатка (причем оба ответа должны быть одинаковы);
4) записать результат с первой точки первым;
5) найти произведение обоих недостатков и результат записать на месте последних точек;
6) заполняем оставшиеся точки нулями;
7) читаем ответ

Рассмотрим пример:
а)9984 ∙ 9999= 99830016
(10000 – 16) ∙ (10000 -1)
1) 9999-16=9983
2)9984-1=9983
3)16 ∙ 1=16
б) 999973-999990=999963000270
(1000000 -27)*(1000000 -10)
1)999973-10=999963
2) 999990-27=999963
3)27 ∙ 10=270
Задание для участников мастер-класса.
Предлагаю Вам попробовать самостоятельно найти произведение чисел: а)9987 ∙ 9994; б) 999981 ∙ 999985

5 прием: Метод решетки Аль – Хорезми ( умножение двузначных чисел на трехзначные).
Аль-Хорезми – это математик, который является прородителем науки алгебры. Мы встречаем его имя, когда произносим слово алгоритм.
Алгоритм вычисления:
1)составить таблицу, в которой в 1 и 2 столбце записать первый множитель, а в 1 и 2 строке записать второй множитель;
2) провести диагонали в каждой клетке;
3) находим произведение 1 столбца и 1 строки;
4) находим произведение 2 столбца и 1 строки;
5) находим произведение 1 столбца и 2 строки;
6) находим произведение 2 столбца и 2 строки;
7) складываем все цифры по диагоналям, если ответ в диагонали получается двузначным, то десяток перебрасываем на следующий разряд.
8) читаем ответ.

Рассмотрим пример:
75 ∙ 86 312 ∙ 45
Задание для участников мастер-класса.
Предлагаю Вам попробовать самостоятельно найти произведение чисел:
54 ∙ 78; 221 ∙ 34

6 прием : Умножение с помощью линий ( линии чертить под углом 45 градусов)
Алгоритм вычисления:
1)десятки множителей представляем в виде линий (сверху - вниз);
2) единицы множителей – линий (снизу- вверх);
3)отметить точки пересечения линий;
4) разделить чертеж на три части: левая, центральная, правая;
5)посчитать точки в каждой части;
6) прочитать ответ.
Рассмотрим пример: 21 ∙ 13=273

6 прием: Русский «Крестьянский» способ .
Данный способ исторически возник на Руси. Этот способ применяли деловые люди, которые занимались торговлей и им нужно было посчитать свою прибыль.
Алгоритм:
1) Записать первый множитель в первом столбце, а второй – во втором;
2)Число, стоящее в первом столбце надо делить на 2, до тех пор пока не получим единицу (если получается остаток, то его надо отбросить);
3)Число, стоящее в правом столбце умножать на 2;
Причем это делаем одновременно;
4)Вычеркнуть те строки слева , в которых получилось четное число;
5)Оставшиеся числа в правом столбце складываем – это и есть ответ.

56 ∙ 82=
Рассмотрим пример: 4735
Задание для участников мастер-класса. Предлагаю Вам попробовать самим найти произведение чисел: 64 ∙ 25; 38 ∙ 45

Детям я говорю: «Легких расчетов вам на экзамене!»
А Вам хочу пожелать здоровья и творческих находок!
Выбор за Вами!
«Это невозможно!» - сказала Причина.
«Это безрассудство!» - заметил Опыт.
«Это бесполезно!» - отрезала Гордость.
«Попробуй…» - шепнула Мечта.
Большое всем спасибо за участие и работу!





