Урок 2 Геометрия-9
Тема: ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ
Цели: ввести понятие вектора, его длины, коллинеарных и равных векторов; научить учащихся изображать и обозначать векторы.
План урока
1. Организационный момент (5 мин.)
2. Объяснение новой темы (20 мин )
3. Решение задач и примеров на закрепление темы ( 10 мин.)
4. Подведение итогов урока ( 3мин.)
5. Домашнее задание ( 2 мин. )
Ход урока
I. . Проверить количество учащихся на уроке, отметить отсуствующих, проверить наличие учебников и тетрадей и учебных принадлежностей.
II. Изучение нового материала (лекция).
Материал пунктов 76 и 77 рекомендуется изложить в виде небольшой лекции с применением разнообразных иллюстративных средств (графопроектор, плакаты, таблицы, рисунки).
1. Понятие векторных величин (или коротко векторов).
2. Примеры векторных величин, известных учащимся из курса физики: сила, перемещение материальной точки, скорость и другие (рис. 240 учебника).
3. Определение вектора (рис. 241, 242).
4. Обозначение вектора - двумя заглавными латинскими буквами со стрелкой над ними, например, АВ, или часто обозначают одной строчной латинской буквой со стрелкой над ней: а, b, с (рис. 243, а, б).
5. Понятие нулевого вектора: любая точка плоскости также является вектором; в этом случае вектор называется нулевым; обозначают:
0=ММ = АА (рис. 243, а).
6. Определение длины или модуля ненулевого вектора АВ.
Обозначение:
АВ (|a|). Длина нулевого вектора а= 0.
7. Найти длины векторов, изображенных на рисунках 243, а и 243, б.
8. Выполнить практические задания № 738, 739.
9. Рассмотреть пример движения тела, при котором все его точки движутся с одной и той же скоростью и в одном и том же направлении (из пп. 77 учебника), рис. 244.
10. Ввести понятие коллинеарных векторов (рис. 245).
11. Определение понятий сонаправленных векторов и противоположно направленных векторов, их обозначение (рис. 246).
12. Нулевой вектор сонаправлен с любым вектором.
13. Определение равных векторов: если aТТв и |a| = |b|, то а = в.
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 740(а) на доске и в тетрадях.
2. Устно решить задачу № 744.
3. Решить задачу № 742.
4. Решить задачу № 745 (выборочно).
5. Устно по заготовленному чертежу решить задачу № 746.
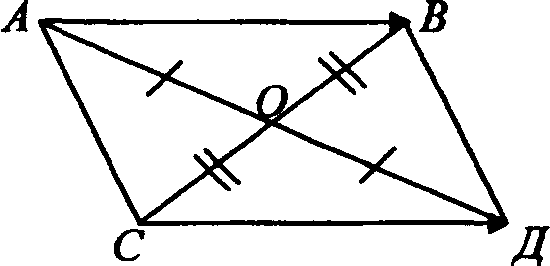
6. Доказать прямое утверждение в задаче № 750:
Доказательство
По условию АВ = СД, то АВ \\ СД, значит, по признаку параллелограмма АВДС - параллелограмм, а диагонали параллелограмма
точкой пересечения делятся пополам, значит, середины отрезков АД и ВС совпадают.
IV. Итоги урока.
V Задание на дом: изучить материал пунктов 76 и 77; ответить на вопросы 1-5, с. 204 учебника; решить задачи № 740(6), 749, 750 (обратное утверждение).





