ГАПОУ ПО ПКИПТ (ИТ - колледж)
Конкурс-игра "Великолепная пятёрка"
Методическая разработка
Пенза
2019
Введение
Инновационная образовательная программа (ИПО), реализуема колледжем, нацелена на развитие продуктивных, творческих способностей студентов для освоения инновационных (общих и профессиональных) компетенций.
Для эффективной реализации обучения в рамках образовательных стандартов нового поколения, основанных на компетенциях, перед преподавателями стоят следующие методические задачи:
 применять активные методы обучения;
применять активные методы обучения;
 создавать условия для самоуправляемого обучения с опорой на практическое приобретение нового опыта.
создавать условия для самоуправляемого обучения с опорой на практическое приобретение нового опыта.
Основной принцип методики активного обучения:
 предоставить возможность учиться поиску, обработке к использованию информации. Методическая разработка конкурса-игры по математике является помощью преподавателям колледжа для эффективной реализации обучения в рамках образовательных стандартов нового поколения, основанных на компетенциях.
предоставить возможность учиться поиску, обработке к использованию информации. Методическая разработка конкурса-игры по математике является помощью преподавателям колледжа для эффективной реализации обучения в рамках образовательных стандартов нового поколения, основанных на компетенциях.
По характеру педагогического процесса конкурс - игра относится к контрольно-обобщающим, по характеру игровой методики - к предметным играм с готовыми правилами, но включает в себя элементы ролевой игры. Игровая среда предполагает использование компьютерной техники и предметов, необходимых для проведения конкурсных заданий. Конкурс-игра рассчитана на обучающихся первого курса. Может проводиться внутри группы, между командами групп.
Конкурс – игра как форма использования игровой технологии во внеурочной предметной деятельности по математике базируется на следующих принципах:
познавательность - способствует расширению кругозора, развитию познавательных умений и навыков, активизации учебной деятельности студентов;
креативность - стимулирует и развивает творческие способности студентов;
развлекательность - вносит в образовательный процесс элемент игры и способствует повышению интереса к предмету;
состязательность - проводится между группами первого курса, создавая здоровую конкуренцию в среде студентов;
общедоступность - в игре принимают участие все студенты группы;
преемственность - проводится с определенной цикличностью в течение нескольких лет.
Конкурс-игра "Великолепная пятёрка" может использоваться в качестве формы внеклассной работы по математике. Требует тщательной подготовки, но даёт значительный положительный результат, к которому стремится каждый педагог. Конкурс-игра может проводиться эпизодически, как разовое состязание для активизации учебной деятельности учащихся, и системно, как вариант обобщения и закрепления знаний по крупной предметной теме, разделу.
Тема конкурса-игры «Великолепная пятёрка»
Цель:
Организовать деятельность студентов по формированию прочных знаний по темам школьного курса математики.
Задачи конкурса-игры:
закрепить и расширить знания по темам школьного курса математики;
развивать внимание, память, речь, мышление;
развивать умение сравнивать, находить аналогии;
развивать воображение, фантазию, творческие способности, эмпатию, рефлексию;
развивать умение пользоваться дополнительными источниками информации;
научиться работать в группе при решении познавательных задач, соотносить свои действия с действиями участников группы, распределять роли в совместной групповой деятельности;
развивать способности действовать в нестандартной ситуации;
подчинять свою деятельность установленным правилам, нормам;
формировать толерантное отношение к соперникам;
развивать умение выступать публично, вести себя на сцене.
Содержание и правила игры
Для игры была разработана символика – эмблемы-медальки, формирующие определённый позитивный стереотип.
Игра осуществляется как состязание команд-пятёрок, но также предполагает активное участие болельщиков, которые по ходу игры отвечают на вопросы, возникающие в процессе развития сценария, и участвуют в конкурсах для болельщиков. От успешной работы болельщиков во многом зависит успешность команды. Поддержка групп может принести дополнительные жетоны команде. В игре участвуют три команды разных групп первого курса.
Проведение игры возлагается на ведущих студентов, оценивание поручается жюри из трёх человек – студентам, не участвующим в игре.
Игра состоит из трёх туров. Первый тур – отборочный (играют три команды), второй тур – близ тур (играют две команды, набравшие большее количество жетонов), третий тур - «Самый сообразительный» - играет одна команда, набравшая большее количество жетонов. Выигрывает студент, набравший большее количество жетонов. Конкурсы каждого тура предполагают вопросы и задания разного уровня сложности, от репродуктивных до творческих, что позволяет дифференцировано подходить к группам разного уровня подготовки и не исключает возможности успеха для всех команд и групп-участников.
Система оценивания исходит из сложности заданий и вопросов и колеблется от 1 до 3-х жетонов за правильный ответ.
Этапы реализации игры
Конкурс - игра "Великолепная пятёрка" предполагает три этапа в ходе её реализации в учебно-воспитательном процессе.
| Этапы | Содержание |
| I. Предварительная подготовка | Подготовка осуществляется на двух уровнях: группами и организаторами |
| II. Проведение игры | Игра проводится с условием, что студенты уже ознакомлены с правилами |
| III. Анализ и рефлексия | Осуществляется на двух уровнях: в группах и организаторами игры |
I. Предварительная подготовка игры.
- Из студентов каждой группы формируются команды по 5 человек. При организации команд необходимо учитывать уровень подготовки студентов (выбираются наиболее успешные в предмете) и добровольное желание студентов принять участие в игре.
- Командам и группе даются заблаговременно задания творческого характера. Организаторы игры готовят рекомендации по их выполнению и оказывают консультативную помощь.
- Организаторы готовят задания и вопросы для игры по конкретной теме и их техническое представление.
- Составляется сценарий проведения игры с включением в него творческих заданий студентов и конкурсов, составленных организаторами, развлекательных пауз.
- Разрабатывается система оценивания участия в игре.
- Готовится система поощрения команд-участниц и групп.
- Студенты информируются о сроках и месте проведения игры.
II. Проведение игры.
- Игра проводится в назначенный срок и длится не более 1,5 часа.
- Судейство осуществляется независимым жюри.
- Результаты игры объявляются сразу после завершения каждого тура.
III. Анализ и рефлексия.
- Анализ игры с изучением мнения студентов проводится не позднее трёхдневного срока со времени её проведения.
- Рефлексия студентов проводится по каждой группе в отдельности.
- С учётом мнения студентов готовятся рекомендации по проведению следующей игры.
Условия проведения игры
- Игровая среда использует большое помещение – актовый зал.
- Помещение оформлено символикой игры, ТСО, необходимым освещением, компьютерной техникой, позволяющей проецировать на экран игровой визуальный ряд.
- Игра проводится с приглашением студентов групп первого курса.
- Оценивание игры осуществляется независимым жюри из трёх человек (система оценок и критерии готовятся заранее).
- Игру проводит, корректирует при необходимости ход игры, осуществляет контроль за соблюдением правил ведущий.
- После двух туров награждается победившая команда - «Великолепная пятёрка», после третьего тура награждается студент - «Самый сообразительный».
Сценарий конкурса - игры "Великолепная пятёрка"
На сцене три стола и стулья для команд. Звучит музыка. На экране заставка "Великолепная пятёрка". Выходят ведущие.
Ведущий 1: Добрый день, дорогие друзья! Приветствую вас на конкурсе - игре "Великолепная пятёрка"! Как вы знаете, значение математики непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенную роль. Она стала не заменимым орудием во всех науках о природе, в технике. В нашу современную жизнь вторгается математика с её особым стилем мышления становящимся сейчас обязательным для всех профессий.
Ведущий 2: Читает стихотворение «Баллада о математике».
Ведущий 1: И вот сейчас мы имеем возможность проверить, насколько каждая команда и участники сегодняшнего конкурса сильны в математике.
.На сцену выходят команды-участники игры под музыкальное сопровождение, занимают игровые места. Участники выносят свою символику.
Ведущий 2: Каждая команда представит себя сама. Оценивать успехи игры мы будем жетонами? Начинается наш первый конкурс отборочного тура "Визитка" (представление команд).
Жюри подводит итог конкурса.
Ведущий 1: Конкурс «Великие математики». Изучая математику, нельзя забывать тех великих людей, которые способствовали её развитию, заложили её основы. Конкурс заключается в том, что каждая команда по описанию какого-либо учёного – математика должна назвать его и пополнить, что знает из биографии. За каждый правильный ответ 1 жетон. Команды дают ответы, руководствуясь правилом «кто первый».
Ведущий 2: Первый шаг сделан. Каковы его результаты, уважаемые жюри?
Слово жюри - подведение итогов конкурса "Великие математики".
Ведущий 1: Конкурс «Головные уборы». Надо сделать любой головной убор, имеющий форму какого-либо геометрического тела и продемонстрировать, дополняя своими комментариями.
Ведущий 2: Конкурс « Парад цифр». Команда выбирает две цифры и через одну минуту показывает эти цифры в живых картинках. За лучшее представление два жетона.
Ведущий 1: Конкурс певцов. За две минуты придумать или вспомнить как можно больше частушек, куплетов из песен, в которых есть числа, и исполнить их. За большее количество, названных куплетов из песен и частушек три жетона.
Ведущий 2: Пришло время проверить основное домашнее задание, которое заключалось в следующем: каждая команда должна инсценировать сказку-задачу, решив её правильно. Посмотрим, как они справились с ней. За лучшую инсценировку три жетона.
Ведущий 1: Вопросы (кто быстрее). (Допускается помощь болельщиков.) За каждый правильный ответ 1 жетон.
1.Отрезок, соединяющий точку окружности с её центром. (Радиус.)
2. Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. (Медиана.)
3.Четырёхугольник, у которого противолежащие стороны параллельны. (Параллелограмм.)
4. Параллелограмм, у которого все стороны равны. (Ромб.)
5.График квадратичной функции. (Парабола.)
6. Прямоугольник, у которого все стороны равны. (Квадрат.)
7. Отношение противолежащего катета к гипотенузе. (Синус.)
8. Мера веса драгоценных камней. (Карат.)
9. Угол, меньший прямого. (Острый.)
10.Параллелограмм, у которого все углы прямые. (Прямоугольник.)
Жюри подводит итог 1 отборочного тура, объявляет результат первого тура. Команда, набравшая меньшее количество жетонов, выходит из игры. В следующем туре, остаются две команды, набравшие большее количество жетонов.
Музыкальная пауза. Песня о математике на мотив песни «Зайка моя» исполняют студенты.
Ведущий 2: Близ – тур. Тур двух пятёрок.
«Математическая эстафета»
Командам по очереди задают по одному вопросу. Время на обдумывание- 30 секунд.
(за каждый правильный ответ – 1жетон.)
Вопросы для первой команды.
1.Результат сложения? (Сумма.)
2. Сколько цифр вы знаете? (Десять.)
3. Наименьшее трёхзначное число? (Сто.)
4. Сотая часть числа. (Процент.)
5. Прибор для измерения углов. (Транспортир.)
6. Сколько сантиметров в метре? (Сто.)
7. Сколько секунд в минуте? (Шестьдесят.)
8. Сколько лет в одном веке? (Сто.)
9. Результат деления? (Частное.)
10. Когда произведение равно нулю? (Когда хотя бы один из множителей равен 0.)
11. График прямой пропорциональности? (Прямая, проходящая через начало координат.)
12. Ордината точки единичной окружности. (Синус.)
13. Величина, обратная косинусу. (секанс.)
14. Что меньше 2\5 или 0,5? (2\5.)
15.Отношение прилежащего катета к противолежащему катету? (Тангенс острого угла.)
16. Корень уравнения 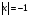 . (Не существует.)
. (Не существует.)
17. Какую часть минуты составляет 15 с? (1\4.)
18. Сколько сантиметров составляет 1% метра? (1см.)
Вопросы для второй команды
Радиус окружности 6см. Диаметр? (12см.)
Какую часть часа составляет 20 мин? (1\3.)
Результат вычитания. (Разность.)
На какое число нельзя делить? (На 0.)
Отношение прилежащего катета к гипотенузе. (Косинус угла.)
Величина, обратная к косинусу. (Косеканс.)
Наибольшее двузначное число? (99.)
Площадь квадрата со стороной а? (а в квадрате.)
Сколько граммов в килограмме?. (1000.)
Сколько минут в часе? (Шестьдесят.)
Результат умножения? (Произведение.)
Сколько часов в сутки? (Двадцать четыре.)
Наименьшее натуральное число? (1.)
График обратной пропорциональности? (Гипербола.)
Что больше: 2м или 201 см? (201см.)
Найдите 10% от тонны ( 100кг.)
Сколько значений имеет угол α,
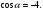 (Ни одного.)
(Ни одного.)Прибор для построения окружности? (Циркуль.)
Жюри подводит итог близ – тура.
Ведущий 2: Краткость и точность математического языка является его отличительной и в то же время красивой чертой. ( За правильно выполненное задание 2 жетона.)
1. В треугольнике АВС, АВ=ВС. Назовите пять терминов, характеризующих отрезок ВД.
2.Употребляя соответствующие математические термины, упростить следующие фразы:
а) многоугольник с наименьшим числом сторон. (Треугольник.)
б) хорда, которая проходит через центр окружности. (Диаметр.)
в) в равнобедренном треугольнике, основание которого равно боковой стороне. (Равносторонний.)
Задание 1: “Сосчитайте фигуры”.
Ведущий 1: У каждой команды лист бумаги, ножницы.
Задание 2: Квадратный лист бумаги разрезать на две равные части, а затем составить из них треугольник. Как это сделать?
Жюри подводит итог 2 отборочного тура, объявляет результат второго тура. Команда, набравшая меньшее количество жетонов, выходит из игры. В следующем туре: «Самый сообразительный» играет одна команда выведенная в финал.
Музыкальная пауза.
Ведущий 1: III тур. «Самый сообразительный»
У каждого участника лист бумаги, ручка для решения задач.
На одну чашку весов положили кусок мыла, а на другую чашку 3\4 такого же мыла и ещё 200г. Весы в равновесии. Какова масса куска мыла. (200г-1/4;200:
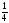 =800г.)
=800г.)Радиус круга 5м. Если считать, что
 =3, то почему S
=3, то почему S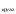 равна 75.
равна 75.Какие числа при перевёртывании увеличиваются в полтора раза? (6,66,666.)
Быстро сосчитайте:1000
+ 30
+1000
+ 40
+1000
+20
+1000
+10 (4100.)
Чему равна площадь закрашенного квадрата?
Как при помощи двух нитей столяр может проверить, лежат ли концы четырех ножек стола в одной плоскости?
Назвать фигуры, между которыми следующий диалог:
- Любую площадь я измерить рад,
Ведь у меня четыре стороны,
И все они равны.
Углы они мне делят пополам,
Ими на части разные разбит я. (Квадрат)
-И у меня равны диагонали! (Прямоугольник)
-Мои хотя и не равны,
Но под прямым углом пересекаются,
Совсем как у квадрата. (Ромб)
-Хоть стороны мои
Попарно и равны, и параллельны.
Всё же я в печали, что не равны мои диагонали,
И углы они не делят пополам. (Параллелограмм)
Ведущий 2:
Вот закончилась игра,
Результат узнать пора.
Кто же лучше всех трудился
И в игре отличился?
Слово жюри. Награждение победителей.
Приложение 1
Стихотворение «Баллада о математике…»
Как воздух, математика нужна,
Самой отваги офицеру мало.
Расчёты! Залп! И цель поражена
Могучими ударами металла.
И воину припомнилось на миг,
Как школьником мечтал в часы ученья;
О подвиге, о шквалах огневых,
О яростном порыве наступленья.
Но строг учитель был,
И каждый раз он обрывал мальчишку грубовато:
-Мечтать довольно, повтори рассказ…
О свойствах круга и углах квадрата.
И воинам любовь сохранена
К учителю далёкому, седому.
Как воздух, математика нужна
Сегодня офицеру молодому.
Эмблемы-медальки


Конкурс «Великие математики».
По описанию какого-либо учёного – математика назвать его и пополнить его биографию.
1.
Самый великий математик и физик античных времён жил в III веке до нашей эры, примерно в 287-211г. Он написал ряд произведений по геометрии и физике. Определил приблизительное значение числа «
 ». Вычислил собственным методом поверхности многих плоских фигур и объёмов тел. Основатель гидростатики. И сегодня известна спираль, закон, аксиома его имени. На могиле этого великого математика был установлен памятник с изображением шара и описанного около него цилиндра. Спустя 200 лет по этому памятнику нашли его могилу. (Архимед).
». Вычислил собственным методом поверхности многих плоских фигур и объёмов тел. Основатель гидростатики. И сегодня известна спираль, закон, аксиома его имени. На могиле этого великого математика был установлен памятник с изображением шара и описанного около него цилиндра. Спустя 200 лет по этому памятнику нашли его могилу. (Архимед).
2. Жил в шестом веке до нашей эры (около 580 - 500 до н. э.) древнегреческий математик и философ - идеалист. Родился на острове Самос. Имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Прозвище философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (…- убеждающий речью".) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали его законы и правила. Самое большее, что известно сейчас народонаселению об этом уважаемом древнем греке, укладывается в одну фразу: … (Пифагор Самосский).

3. Французский математик - будущий преобразователь алгебры появился на свет в маленьком французском городке недалеко от крепости Ла-Рошель. Жизнь его проходила на фоне кровавых событий войны, которую вели две мощные религиозные группировки католиков и гугенотов. Жил в 16 веке (1540-1603г), внёс огромный вклад в развитие алгебраической символики: в его работах имеется вывод формулы корней квадратного уравнения и их свойств, сформулирована теорема косинусов. группировки католиков и гугенотов. Сейчас нам трудно представить математику без его формул и уравнений. (Франсуа Виет )

4.
. Жил в 1643-1727г.г. Наружность его была невзрачной. Одевался он всегда просто. Никогда не носил очков и до самой смерти (он умер в 85 лет) имел густые волосы, скрытые под париком. В последние годы потерял один зуб. В Вестминстерском аббатстве надпись на его надгробии заканчивалась словами «Пусть смертные радуются, что существовало такое украшение рода человеческого…». (Исаак Ньютон).
5.
И с другом, и с врагом ты должен быть хорош! Кто по натуре добр, в том злобы не найдёшь. Обидишь друга- наживёшь врага ты Врага обнимешь- друга обретёшь. Будь мудр и жалкий путь глупца себе не выбирай. Коль щедр друг, в друзья скупца себе не выбирай. Сердца людей открыты тем, кто помыслами чист. Дари всем благо, но льстеца себе не выбирай. Не смотри, что иной выше всех по уму. А смотри верен слову ли он своему. Если он своих слов не бросает на ветер - Нет цены, как ты сам понимаешь ему. Изначальней всего остального – любовь, В песне юности первое слово – любовь. ( Омар Хайям).
Конкурс инсценированных сказок-задач.
1. «Делёж верблюдов».
Старик, имевший трех сыновей, распорядился, чтобы они после его смерти поделили принадлежащее ему стадо верблюдов так, чтобы старший взял половину всех верблюдов, средний – треть и младший девятую часть всех верблюдов. Старик умер и оставил 17 верблюдов. Сыновья начали делёж, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. В недоумении, как им быть, братья обратились к мудрецу. Тот приехал к ним на собственном верблюде и разделил по завещанию. Как он это сделал?
Решение
Мудрец пустился на уловку. Он прибавил к стаду на время своего верблюда, тогда их стало 18. Разделив это число, как сказано в завещании (старший брат получил 9 верблюдов, средний – 6 верблюдов, младший – 2 верблюда), мудрец взял своего верблюда обратно (9 + 6 + 2 +1 = 18).
2. Два пастуха.
Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: « Отдайка ты мне одну овцу, тогда у меня будет ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: « Нет лучше ты мне отдай одну овцу, тогда у нас будет овец
поровну!». Сколько же было у каждого овец?
Ответ: У Ивана было 7 овец, у Петра — 5.
3. Возраст дедушки.
Внук и дедушка
Внук. Сколько тебе лет?
Дедушка. Если я проживу еще половину того, что я прожил, да еще 1 год, то мне будет 100 лет. Вот и считай!
Внук. Да! Ну и задачку ты мне задал! Попробую решить.
Ответ: Возраст дедушки 66 лет.
При решении задачи поможет схема.
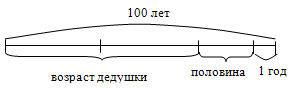
100 – 1 = 99 (лет).
Годы дедушки и их половина вместе составляют 99 лет. А это 3 части. Значит 1 часть составляет 99 : 3 = 33 года.
33 года – половина того, что прожил дедушка.
33 · 2 = 66 лет – возраст дедушки.
Песня о математике на мотив песни «Зайка моя».
Плюсик ты мой, я - твой минус,
Косинус ты, я - твой синус,
Ты аксиома, я - теорема,
Следствие ты, а я - лемма.
Ма-те-ма-ти-ка моя...
Припев:
Я ночами плохо сплю,
Математику я так люблю.
Математику я так давно, давно люблю,
Я и днем теперь не сплю,
Я и вечером не сплю,
Все учу, учу, учу, учу, учу.
2. Знание ты, я - шпаргалка.
Если ты нуль, то я - палка.
Ты ордината, то я - абсцисса,
Ты уголок, я - биссектриса.
Ма-те-ма-ти-ка моя...
3. Частное ты, я - делитель.
Ты знаменатель, я - числитель.
Ты мой кружок, я - твой сектор,
Ты модуль мой, я - твой вектор.
Ма-те-ма-ти-ка моя...
4. Сумма моя, а я - разность,
Дольная ты, а я — кратность,
Гипотенуза ты, я - твой катет,
Терминов нам с тобой хватит.
Ма-те-ма-ти-ка моя...
Приложение II
Краткость и точность математического языка является его отличительной и в то же время красивой чертой.
 1. В треугольнике АВС, АВ=ВС. Назовите пять терминов, характеризующих отрезок ВД. В
1. В треугольнике АВС, АВ=ВС. Назовите пять терминов, характеризующих отрезок ВД. В
А С
Д
Задание 1: “Сосчитайте фигуры”.
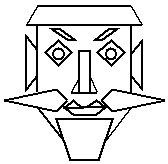
1 2  Задание 2: Задание: Квадратный лист бумаги разрезать на две равные части, а затем составить из них треугольник. Как это сделать?
Задание 2: Задание: Квадратный лист бумаги разрезать на две равные части, а затем составить из них треугольник. Как это сделать?
Частушки о математике
Мы с подружкою вдвоём
Вам частушки пропоём.
Раз, два, три, четыре, пять,
Так с чего же нам начать?
Математика – наука
Замечательная штука.
Будем, будем изучать
Математику на 5!
Скорость лошадей узнали
И в ответе написали:
«Мчится лошадь без кареты
В тысячу раз быстрей ракеты».
Мы таблицы умноженья
Взяли и попрятали.
Дайте нам для ускоренья
Микрокалькуляторы.
Геометрию люблю.
Видиков не надо,
В теореме Пифагора,
Вся моя отрада.
Уравнение, уравнения
До чего вы довели
Иксы, минусы, деление-
Вы меня с ума свели
Уравнение решать-
Дело непростое.
Плюс на минус поменять-
Правило такое.
Извлекали мы квадрат
Из числа обычного,
Только вышел результат
Весьма неприличный.
Мы частушки вам пропели
хорошо ли, плохо ли,
А теперь мы вас попросим,
Чтоб вы нам похлопали.
Приложение III
Чему равна площадь закрашенного квадрата?
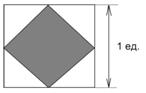
Заключение.
Конкурс-игра "Великолепная пятёрка" может использоваться в качестве формы внеаудиторной работы по математике. Игра требует тщательной подготовки, но даёт значительный положительный результат, к которому стремится каждый педагог. Игра может проводиться эпизодически, как разовое состязание для активизации учебной деятельности студентов, и системно, как вариант обобщения и закрепления знаний по крупной предметной теме, разделу.
Рекомендуется проводить игру "Великолепная пятёрка" в ходе предметных недель в школе. Это позволяет привлечь для организации и проведения игры нескольких преподавателей - предметников, а также сделает предметную неделю интересной, насыщенной и запоминающейся для студента.
При достаточно хорошей организации и подготовке игра может проводиться как элемент диагностики уровня подготовленности студентов, выявления и создания условий для развития и реализации творческих способностей одарённых студентов.
Литература:
1. Балх М.Б., Балх Г.Д. “Математика после уроков”
2. Шустеф Ф.М. “Материал для внеклассной работы по математике”
3. Мартин Гартнер “Математические досуги”
4. Игнатьев Е.А. “В царстве смекалки”
5. Мазаник А.А. “Реши сам”
6. Вульфов Б. З., Поташник М. М. «Организатор внеклассной и внешкольной воспитательной работы», М. «Просвещение», 1983.
7. Василевский А. Б. «Задания для внеклассной работы по математике», Минск: 1988.
8. Литцман В. «Веселое и занимательное о числах и фигурах», М.: 1963.
9. Журнал "Математика в школе ".
10. Гейлер Г. И. История математики в школе / Москва, Изд-во “Просвещение”, 1964

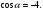 (Ни одного.)
(Ни одного.)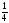 =800г.)
=800г.)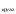 равна 75.
равна 75.



