
Взаимное расположение прямых в пространстве. Угол между двумя прямыми.

Скрещивающиеся прямые
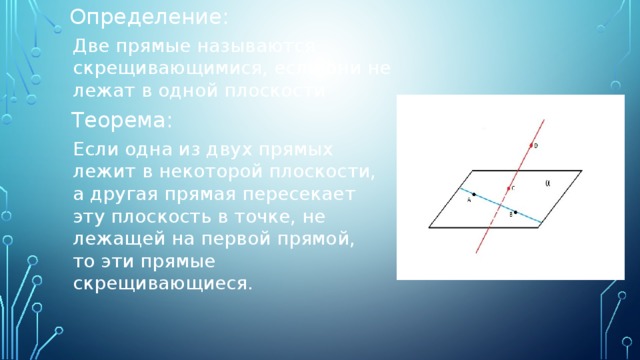
Определение:
Две прямые называются скрещивающимися, если они не лежат в одной плоскости
Теорема:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
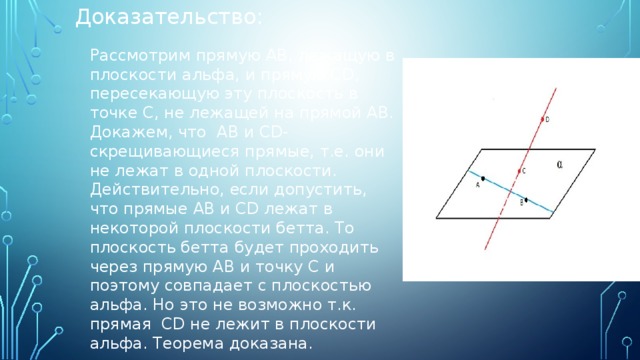
Доказательство:
Рассмотрим прямую AB, лежащую в плоскости альфа, и прямую CD, пересекающую эту плоскость в точке С, не лежащей на прямой AB. Докажем, что AB и CD-скрещивающиеся прямые, т.е. они не лежат в одной плоскости. Действительно, если допустить, что прямые AB и CD лежат в некоторой плоскости бетта. То плоскость бетта будет проходить через прямую AB и точку С и поэтому совпадает с плоскостью альфа. Но это не возможно т.к. прямая CD не лежит в плоскости альфа. Теорема доказана.
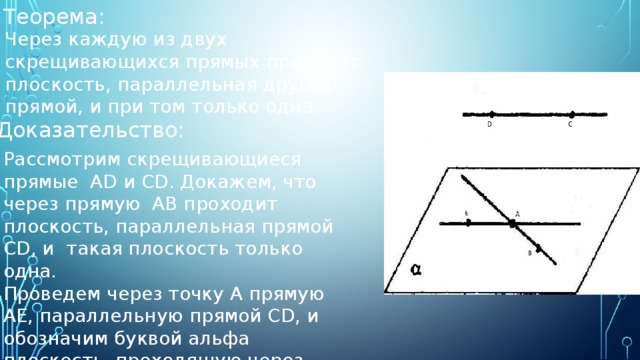
Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и при том только одна.
Доказательство:
Рассмотрим скрещивающиеся прямые AD и СD. Докажем, что через прямую AB проходит плоскость, параллельная прямой CD, и такая плоскость только одна.
Проведем через точку А прямую АЕ, параллельную прямой CD, и обозначим буквой альфа плоскость, проходящую через прямые AB и AE.
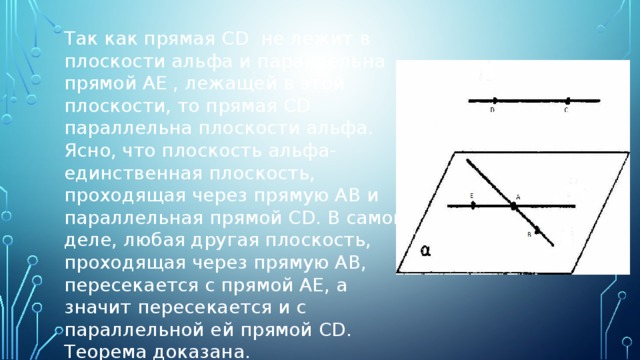
Так как прямая CD не лежит в плоскости альфа и параллельна прямой АЕ , лежащей в этой плоскости, то прямая CD параллельна плоскости альфа.
Ясно, что плоскость альфа-единственная плоскость, проходящая через прямую AB и параллельная прямой CD. В самом деле, любая другая плоскость, проходящая через прямую AB, пересекается с прямой AE, а значит пересекается и с параллельной ей прямой CD. Теорема доказана.

Углы с сонаправленными сторонами
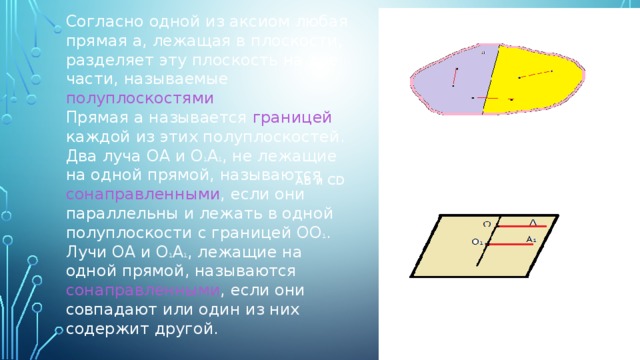
Согласно одной из аксиом любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями
Прямая а называется границей каждой из этих полуплоскостей.
Два луча ОА и О 1 А 1 , не лежащие на одной прямой, называются сонаправленными , если они параллельны и лежать в одной полуплоскости с границей ОО 1 .
Лучи ОА и О 1 А 1 , лежащие на одной прямой, называются сонаправленными , если они совпадают или один из них содержит другой.
AB и CD

Теорема:
Если стороны двух углов соответственно сонаправлены, то такие углы равны.
Доказательство:
Рассмотрим углы О и О 1 с соответственно сонаправленными сторонами и докажем, что угол О=углу О 1 .
Отметим на сторонах угла О точки А и В и отложим на соответственных сторонах угла О 1 отрезки О 1 А 1 =ОА и О 1 В 1 =ОВ.
Четырехугольник ОО 1 А 1 А-параллелограмм, т.к. противоположные стороны ОА и О 1 А 1 параллельны и равны. Отсюда следует , что АА 1 ||ОО 1 и АА 1 ||ОО 1 . Аналогично четырехугольник ОО 1 В 1 В-параллелограмм, поэтому ВВ 1 ||ОО 1 и ВВ 1 =ОО 1 . Т.к. АА 1 ||ОО 1 и ВВ 1 ||OO 1 , то по теореме о трех параллельных прямых АА 1 ||ВВ 1 . кроме того, АА 1 =ОО 1 =ВВ 1 . таким образом, в четырехугольнике АВВ 1 А 1 противоположные стороны АА 1 и ВВ 1 параллельны и равны. Следовательно, этот четырехугольник-параллелограмм, и значит, стороны А 1 В 1 и АВ равны. Сравним теперь треугольники АОВ и А 1 О 1 В 1 . Они равны по трем сторонам, и поэтому угол О=углу О 1 . Ч.Т.Д.





