тЕма урока: «Прямая и обратная пропорциональные зависимости»
Цель урока:
ввести понятие прямой пропорциональной зависимости и научить решать задачи, используя прямо пропорциональную зависимость величин;
закрепить навыки решения уравнений с помощью пропорции, формирование чувства ответственности, воспитание самостоятельности учащихся, увеличение степени дисциплинированности, организованности, стимулирование «я – концепции», развитие общественно – активной личности, внедрение ситуации «успеха» в образовательный процесс, развитие индивидуальных особенностей учащихся.
развитие умений применять математические знания для решения практических задач, формирование необходимости изучения математики для любой категории обучающихся.
Ход урока:
| №, п/п | Этапы урока | Содержание урока | Деятельность учителя | Деятельность ученика |
| 1. | Организационный момент |
| Приветствие учащихся, проверка готовности к уроку. |
|
| 2. | Проверка домашней работы |
|
| |
| 3. | Устная работа | 1. Решить устно № 795 (а; в; д). 2. Какие величины называют прямо пропорциональными? Можно ли считать прямо пропорциональными величины: а) время движения и путь, пройденный теплоходом, идущим со скоростью 18 км/ч; б) объем бензина и его массу; в) количество метров материи и ее стоимость при одной и той же цене; г) приведите пример прямо пропорциональных величин. 3. Решить задачи, составив пропорцию: а) Четыре гнома посадили для Белоснежки 8 кустов роз. Сколько кустов роз посадят за то же время три гнома? Ответ: 6 кустов. б) Велосипедист за 3 ч проезжает 75 км. За сколько времени проедет велосипедист 125 км с той же скоростью? Ответ: 5 ч.
|
| Учащиеся отвечают на вопросы |
| 3. | Изучение новой темы | 1. Разобрать по учебнику решение задачи на с. 128 (2-я часть): Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч… 2. Ввести понятие обратно пропорциональных величин. Привести свои примеры. 3. Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Это свойство обратно пропорциональных величин используется при решении задач. 4. Разобрать решение задачи 2 на с. 129 учебника. 5. Решить задачу (объясняет учитель): Два каменщика могут сложить стену за 15 дней. За сколько дней могут сложить эту стену 5 каменщиков при той же производительности труда? Решение.
Ответ: 6 дней.
|
|
|
| 4. | Физкульминутка |
|
|
|
| 5. | Закрепление | 1. Решить № 782 (д; е) устно. 2. Решить № 782 (ж; з; в) устно. 3. Решить задачу № 786 на доске и в тетрадях. Решение.
Зависимость между количеством машин и их грузоподъемностью обратно пропорциональная.
Ответ: 40 машин. 5. Решить задачу № 785 (с комментированием). Решение.
Ответ: 150 мин. 6. Решить задачи самостоятельно (с помощью пропорции). а) Мотоциклист проехал 3 ч со скоростью 60 км/ч. За сколько часов он проедет то же расстояние со скоростью 45 км/ч? Ответ: 4 ч. б) Три ученика пропололи грядку за 4 часа. За сколько часов выполнят работу два ученика? Ответ: 6 ч. 7. Упростите выражение
| Не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, рост ребенка увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, так как при удвоении возраста рост ребенка не удваивается. |
|
| 6. | Домашнее задание | № 812, 808 (а), |
|
|
| 7. | Итог урока | 1. Вопросы к пункту 22 на с. 130 учебника. 2. Можно ли считать обратно пропорциональными величинами: а) время и количество голов скота, которое можно прокормить запасенным количеством корма; б) цену товара и количество товара, которое можно купить на определенную сумму денег?
|
|
|
.
.
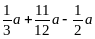и найдите его значение при а = 1,6.
