
Сфера и шар
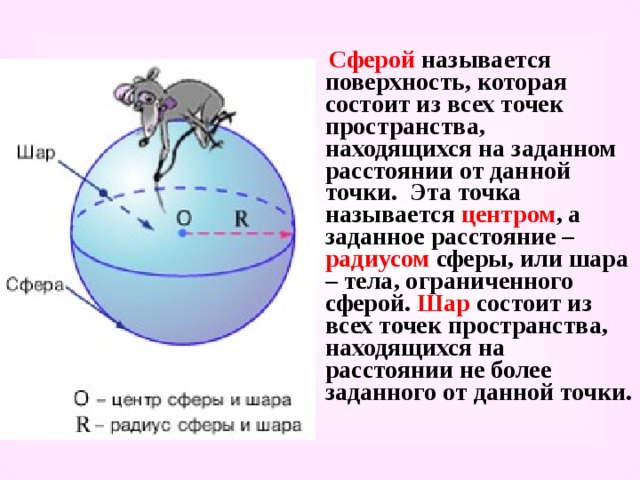
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром , а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
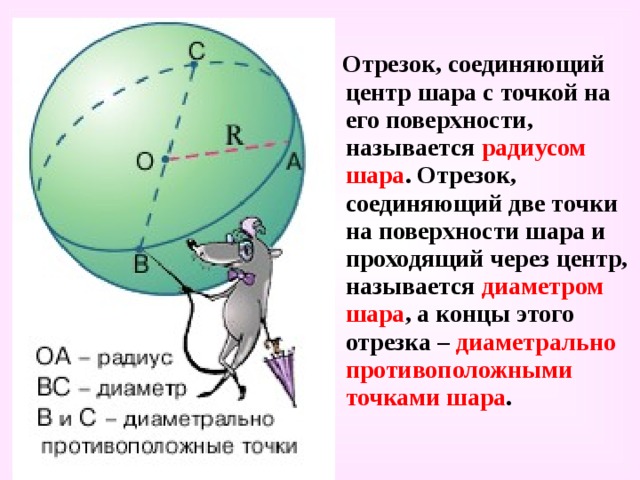
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара . Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара , а концы этого отрезка – диаметрально противоположными точками шара .
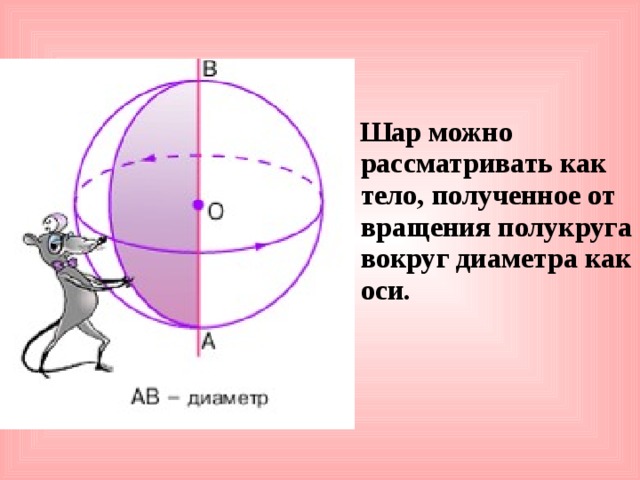
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.
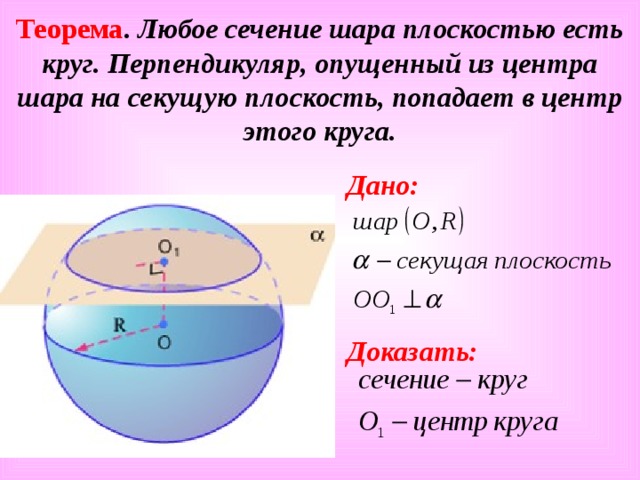
Теорема . Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.
Дано:
Доказать:
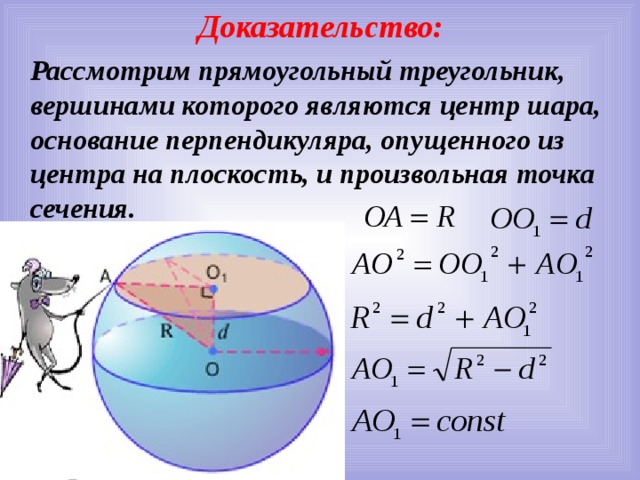
Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.

Следствие . Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.





