
ПРИЗМА

Оглавление
- Определение
- Элементы призмы
- Свойства призмы
- Виды призм
- Призмы в сооружениях
Определение
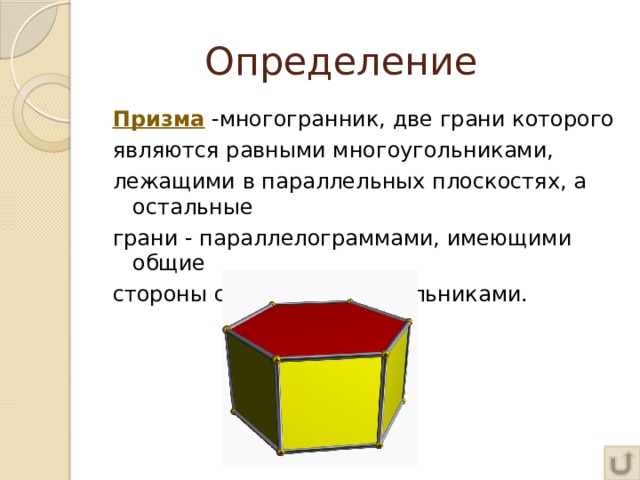
Призма -многогранник, две грани которого
являются равными многоугольниками,
лежащими в параллельных плоскостях, а остальные
грани - параллелограммами, имеющими общие
стороны с этими многоугольниками.

Элементы призмы
- Основания - две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях ( ABCDE, KLMNP).
- Боковые грани - все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом ( ABLK, BCML, CDNM, DEPN, EAKP ).
- Боковая поверхность - объединение боковых граней.
- Полная поверхность - объединение оснований и боковой поверхности.
- Боковые ребра - общие стороны боковых граней ( AK, BL, CM, DN, EP).
- Высота - отрезок, соединяющий основания призмы и перпендикулярный им ( KR) .
- Диагональ - отрезок, соединяющий две вершины призмы, не принадлежащие одной грани ( BP) .
- Диагональная плоскость - плоскость, проходящая через боковое ребро призмы и диагональ основания.
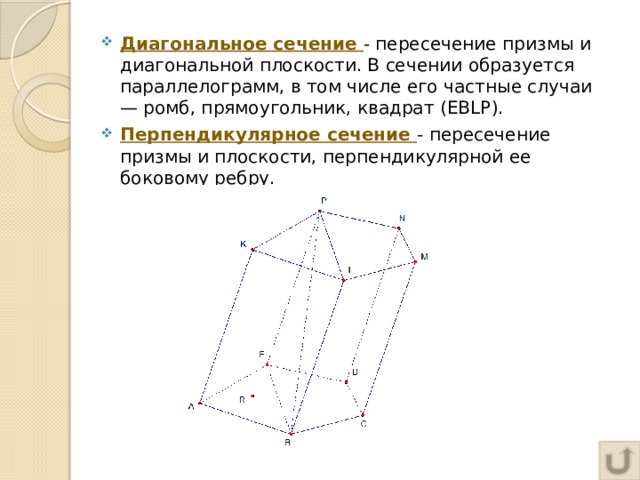
- Диагональное сечение - пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат ( EBLP) .
- Перпендикулярное сечение - пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства призмы
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
V = S ∙ h
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
- Площадь боковой поверхности произвольной призмы S = P ∙ l , где P - периметр перпендикулярного сечения, l - длина бокового ребра.
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Виды призм
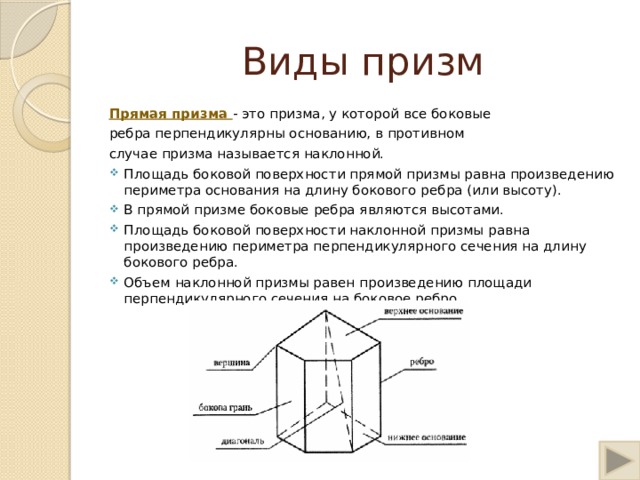
Прямая призма - это призма, у которой все боковые
ребра перпендикулярны основанию, в противном
случае призма называется наклонной.
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или высоту).
- В прямой призме боковые ребра являются высотами.
- Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
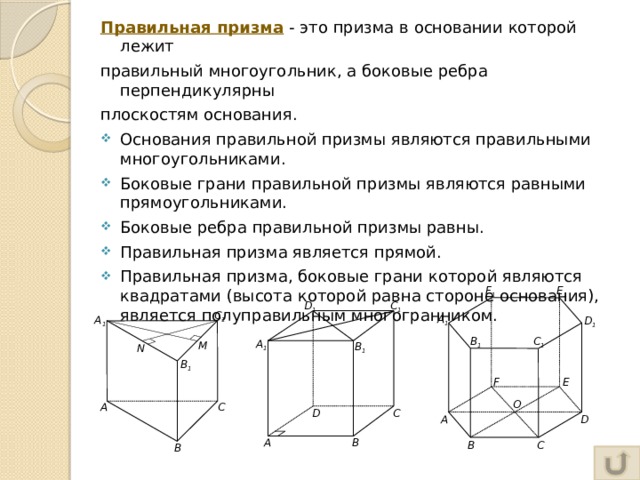
Правильная призма - это призма в основании которой лежит
правильный многоугольник, а боковые ребра перпендикулярны
плоскостям основания.
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны.
- Правильная призма является прямой.
- Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
F 1
E 1
C 1
D 1
C 1
A 1
A 1
D 1
C 1
B 1
A 1
M
B 1
N
B 1
F
E
O
C
A
C
D
A
D
B
A
C
B
B






