
8 класс
18.11.18г

«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать»
Г. Галилей

Истинно или ложно?
- Радиус окружности перпендикулярен прямой, которая является касательной.
- Прямая является секущей по отношению к окружности, если она пересекает окружность в двух точках.
- Прямая проходящая через конец радиуса лежащий на окружности, является касательной к этой окружности.

Теория:
- Теорема о свойстве касательной.
- Теорема о свойстве отрезков касательных к окружности, проведённых из одной точки.
- Теорема - признак касательной.
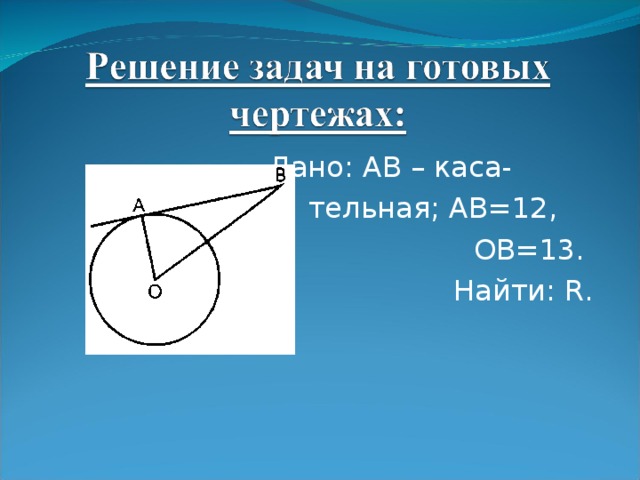
Дано: AB – каса-
тельная; AB=12,
OB=13.
Найти: R.
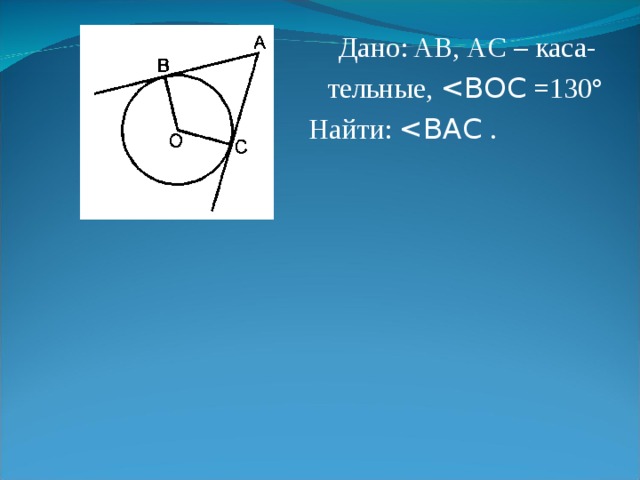
Дано: AB, АC – каса-
тельные,
Найти:
Решение задач
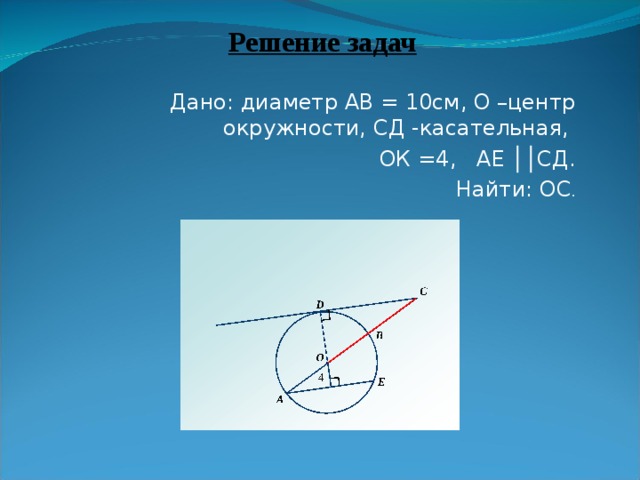
Дано: диаметр АВ = 10см, О –центр окружности, СД -касательная,
ОК =4, АЕ ││СД.
Найти: ОС .
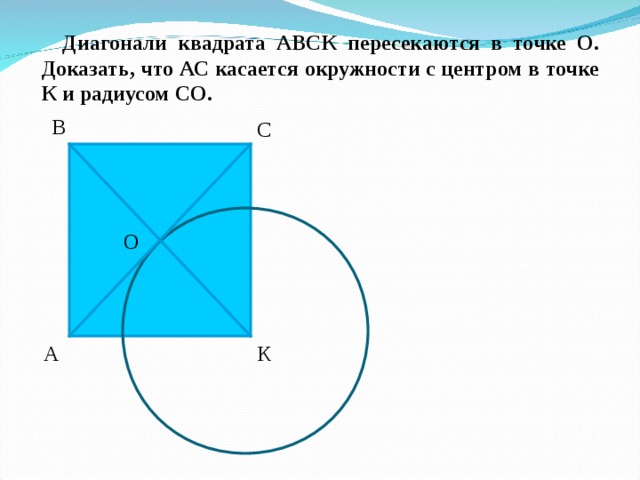
Диагонали квадрата АВСК пересекаются в точке О. Доказать, что АС касается окружности с центром в точке К и радиусом СО.
В
С
О
А
К

Самостоятельная работа
Вариант 1
1. Прямая КЕ касается окружности с центром в точке О, К – точка касания. Найдите ОЕ, если КЕ =8 см, а радиус окружности равен 6 см.
2. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, если ОАВ=30 0 , АВ=5 см.
Вариант 2
1.Найдите N О. Если М N касается окружности с центром в точке О, М точка касания, радиус окружности равен 5 см, М NO = 3 0 0 .
2. Дано: M, N, K – точки касания. Найти: Р треугольника
АВС

Ответы
Вариант2
1) NO = 10 см
2) МВ = В N =4, NC=KC=8 ,
АМ= АК=5. АВ=9,
ВС = 12, АС=13.
Р = 9+ 12 + 13 = 34.
Вариант1
1) ОЕ = 10 см
2) ОАВ = ОАС =30°,
АВ=АС, значит АВС –равнобедренный,
АВС = АСВ =(180°-60°):2 =60°. Значит АВ=АС=ВС. ВС=5.

Домашнее задание:
п. 68 – 69(теория), № 646(а),
№ 645,
№ 648.

Применение касательной
Машиностроение
Применение касательной
Баллистика
Применение касательной
Архитектура
Применение касательной
Медицина
Применение касательной
Физика





