
Симметрия в пространстве

Симметрия, как бы широко или узко мы ни понимали это слово, есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.
Герман Вейль.

Симметрия – свойство формы или расположения фигур. Происходит от греческого «Symmetria» - соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра

История симметрии
Однако как люди дошли до такой сложной и одновременно такой простой вещи, как симметрия?
Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин который сейчас перешёл в русское слово «симметрия»
А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией . Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
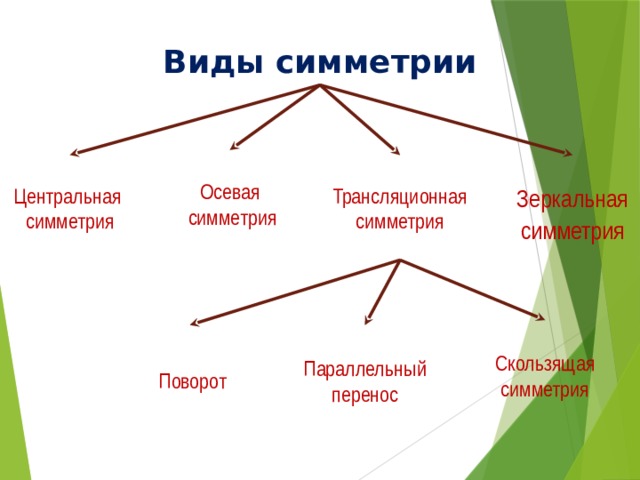
Виды симметрии
Трансляционная
Центральная
Зеркальная симметрия
симметрия
симметрия
Осевая
симметрия
Скользящая симметрия
Параллельный перенос
Поворот
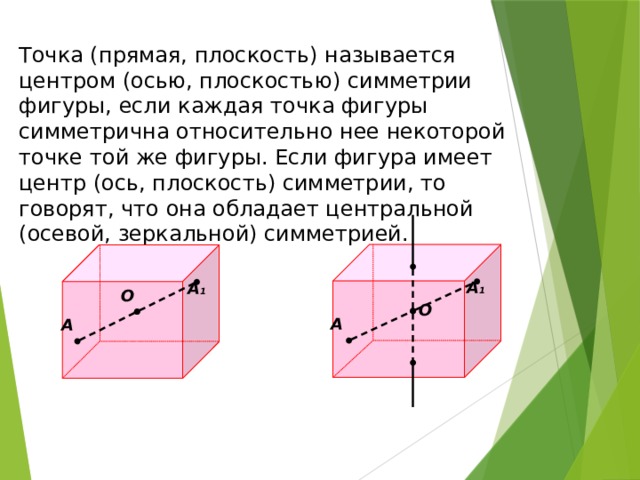
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
А 1
А 1
О
О
А
А
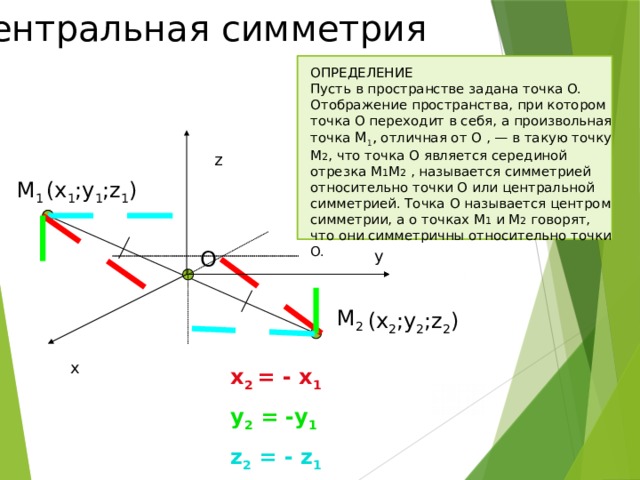
Центральная симметрия
ОПРЕДЕЛЕНИЕ
Пусть в пространстве задана точка О. Отображение пространства, при котором точка О переходит в себя, а произвольная точка М 1 , отличная от О , — в такую точку M 2 , что точка О является серединой отрезка M 1 M 2 , называется симметрией относительно точки O или центральной симметрией. Точка O называется центром симметрии, а о точках M 1 и M 2 говорят, что они симметричны относительно точки O.
z
(х 1 ;y 1 ;z 1 )
М 1
y
О
М 2
(х 2 ;y 2 ;z 2 )
x
x 2 = - x 1
y 2 = -y 1
z 2 = - z 1
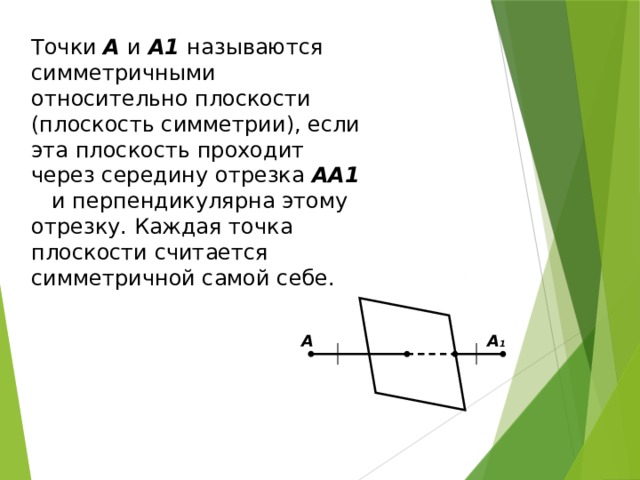
Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.
А
А 1
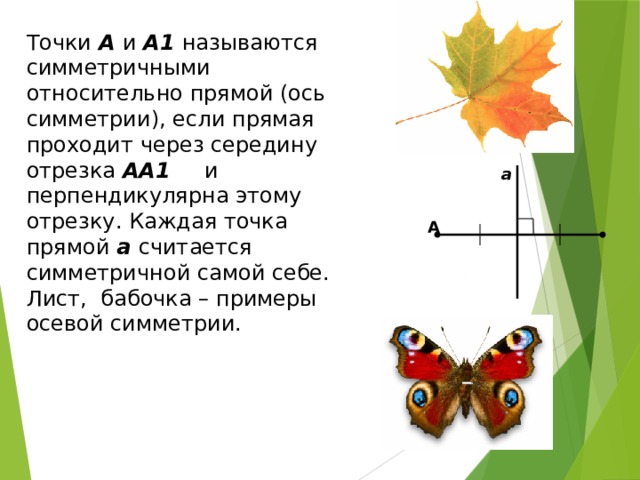
Точки А и А1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе. Лист, бабочка – примеры осевой симметрии.
а
А

Осевая симметрия
ОПРЕДЕЛЕНИЕ
Точка M 1 , не лежащая на прямой l , называется симметричной точке M 2 относительно прямой l , если прямая l является серединным перпендикуляром к отрезку M 1 M 2 .
Если точка лежит на прямой l, то говорят, что точка M 1 симметрична самой себе относительно прямой l .
Прямая l называется осью симметрии .
l
z
(х 1 ;y 1 ;z 1 )
М 1
y
x 2 = - x 1
y 2 = - y 1
z 2 = z 1
(х 2 ;y 2 ;z 2 )
М 2
x
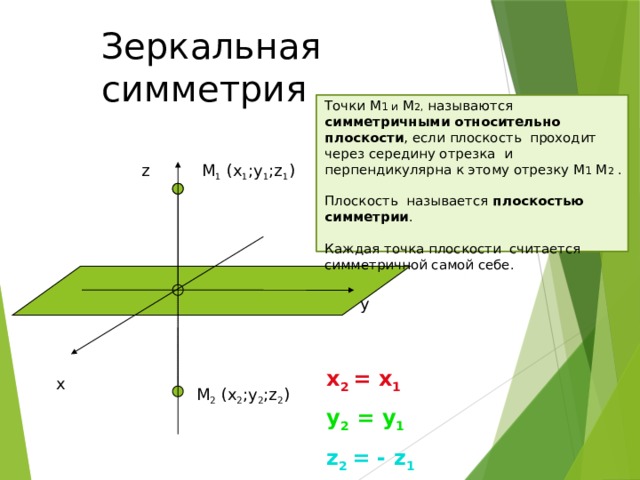
Зеркальная симметрия
Точки M 1 и M 2, называются симметричными относительно плоскости , если плоскость проходит через середину отрезка и перпендикулярна к этому отрезку M 1 M 2 .
Плоскость называется плоскостью симметрии .
Каждая точка плоскости считается симметричной самой себе.
z
M 1 (x 1 ;y 1 ;z 1 )
у
x 2 = x 1
y 2 = y 1
z 2 = - z 1
х
M 2 (x 2 ;y 2 ;z 2 )
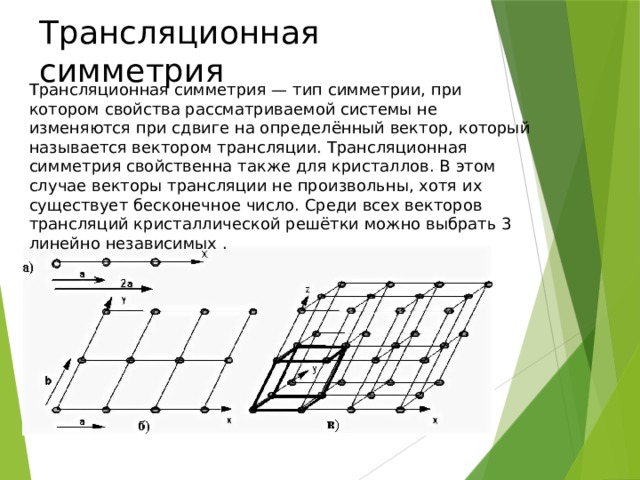
Трансляционная симметрия
Трансляционная симметрия — тип симметрии, при котором свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 линейно независимых .
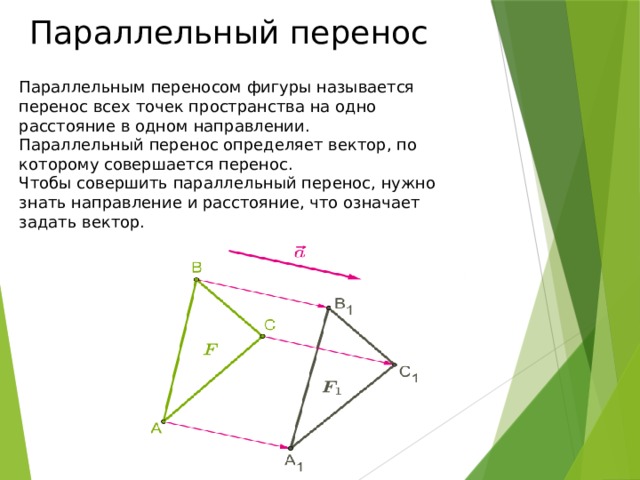
Параллельный перенос
Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.
Параллельный перенос определяет вектор, по которому совершается перенос.
Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.
Поворот
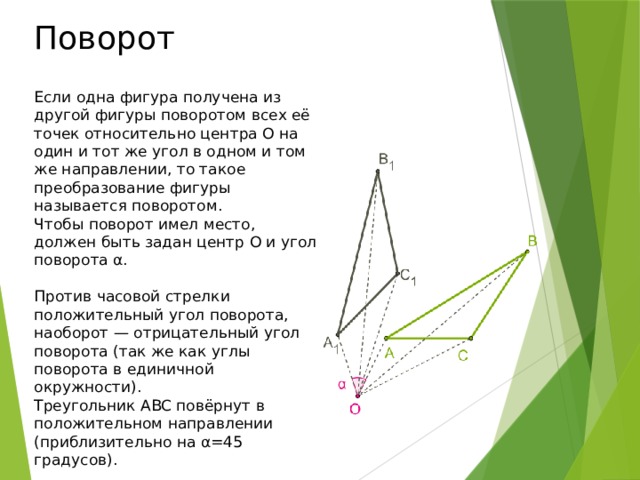
Если одна фигура получена из другой фигуры поворотом всех её точек относительно центра O на один и тот же угол в одном и том же направлении, то такое преобразование фигуры называется поворотом.
Чтобы поворот имел место, должен быть задан центр O и угол поворота α.
Против часовой стрелки положительный угол поворота, наоборот — отрицательный угол поворота (так же как углы поворота в единичной окружности).
Треугольник ABC повёрнут в положительном направлении (приблизительно на α=45 градусов).

Скользящей симметрией
Скользящей симметрией называют композицию симметрии относительно некоторой прямой и переноса на вектор (возможно, нулевой), параллельный этой прямой.
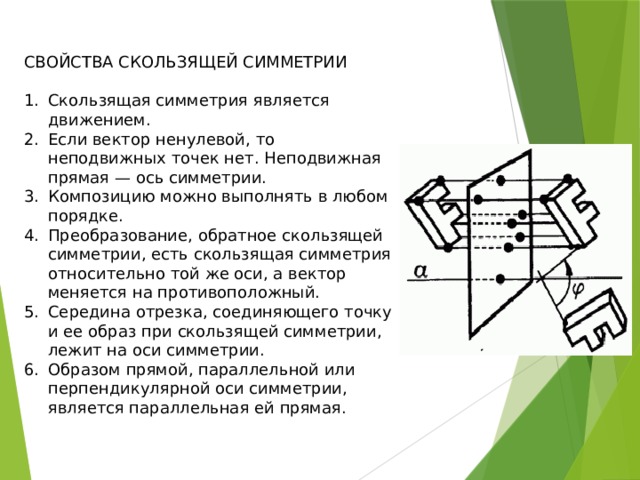
СВОЙСТВА СКОЛЬЗЯЩЕЙ СИММЕТРИИ
- Скользящая симметрия является движением.
- Если вектор ненулевой, то неподвижных точек нет. Неподвижная прямая — ось симметрии.
- Композицию можно выполнять в любом порядке.
- Преобразование, обратное скользящей симметрии, есть скользящая симметрия относительно той же оси, а вектор меняется на противоположный.
- Середина отрезка, соединяющего точку и ее образ при скользящей симметрии, лежит на оси симметрии.
- Образом прямой, параллельной или перпендикулярной оси симметрии, является параллельная ей прямая.





