[8]; б) 
[6].
[2]; б) 
[1].
[0]
; 6) 
; 7)12,05; 8)
; 9)
; 0) ?.
; Х= 160 (км)
(ч) 
Дистанционная олимпиада по математике 2 класс
Рекомендуемое время выполнения заданий ̶ 40 мин.
1. Термометр за окном показывает 9 градусов мороза.
А сколько градусов покажут 2 таких термометра?
А) 9 Б)18 В) 15 Г) 0
2
. В вазе лежали 12 мандаринов. Все, кроме десяти съели. Сколько мандаринов осталось в вазе?
А) 9 Б) 2 В) 10 Г) 12
3. К новогоднему концерту второклассники подготовили 4 номера – танцы и песни. Причем песен было больше, чем танцев. Сколько песен споют второклассники?
А) 4 Б) 3 В) 5 Г) 6
4
. Дедушка Мороз укладывал в коробки подарки для 10 зайчат. В каждую коробку входило не более трёх подарков. Какое наименьшее количество коробок понадобится Дедушке Морозу, чтобы положить в них все подарки?
А) 4 Б) 3 В) 5 Г) 6
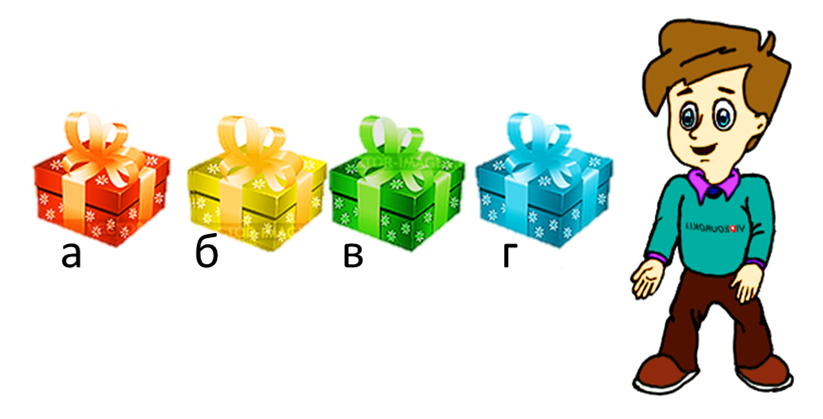5. К празднику Дед Мороз принес подарки всем членам семьи. Андрюше он принёс новый конструктор.
В какой коробке лежит конструктор, если известно, что он лежит не в зелёной коробочке, а красная коробка находится возле коробки с конструктором слева от нее.
А) а Б) б В) в Г) г
6
. Похитил Кощей Бессмертный Снегурочку и спрятал в своём замке. Но дети пошли освобождать Снегурочку. Пришли в замок Кощея, увидели ледяной ключ и три двери. На каждой двери надпись. Дети знали, что хитрый Кощей специально сделал ложные надписи на дверях. Ключом можно открыть только одну из них, а потом ключ растает. Какую дверь должны открыть ребята, чтобы освободить Снегурочку?
А) а Б) б В) в
7
. В зрительном зале в каждом ряду по 17 стульев. Номера на стульях стёрлись. У девочки 10 место, но она зашла в зал с той стороны, где последнее место. На какой по счёту стул она должна сесть, чтобы оказаться на своём месте?
А) 5 Б) 6 В) 7 Г) 8
8
. В коробке лежит 9 ёлочных шаров – 4 красных и 5 золотых. Какое наименьшее количество шаров можно взять из коробки, не глядя в неё, чтобы среди них обязательно был хотя бы 1 золотой шар?
А) 1 Б) 2 В) 4 Г) 5
9
. Оля, Света, Костя и Юра вырезали снежинки. Всего вырезали 10 снежинок, причём каждый из них вырезал разное количество снежинок. Оля вырезала больше всех, а Света меньше всех. Выбери правильное утверждение.
А) девочки вместе вырезали больше, чем мальчики
Б) девочки вместе вырезали столько же, сколько и мальчики
В) мальчики вместе вырезали больше, чем девочки
1
0. На двух тарелках лежало по 15 конфет. С первой тарелки Петя взял 6 конфет, а со второй Наташа взяла столько, сколько осталось на первой тарелке. Сколько всего конфет осталось на обеих тарелках вместе?
А) 15 Б) 10 В) 12 Г) 6
2
