
ГАПОУ КО «Калужский колледж экономики и технологий»
Презентация по математике
на тему:
Выполнила студентка группы Д-21
Малороева Хава
Руководитель: Лавриеня
Елена Анатольевна
Калуга, 2019

Цилиндром (точнее, круговым цилиндром) называется тело, которое состоит из двух кругов , не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков , соединяющих соответствующие точки этих кругов.
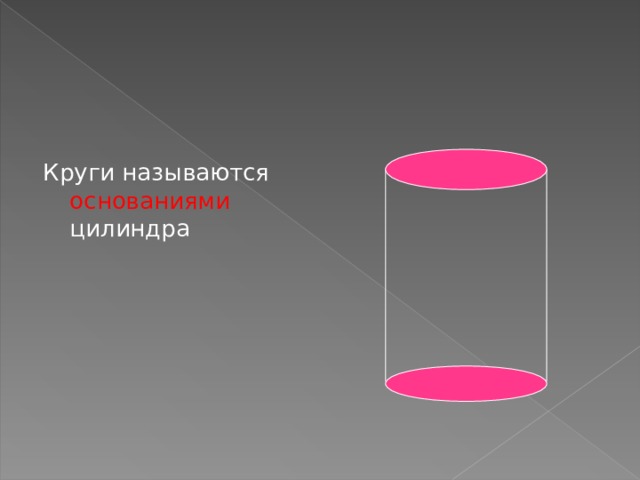
Круги называются основаниями цилиндра
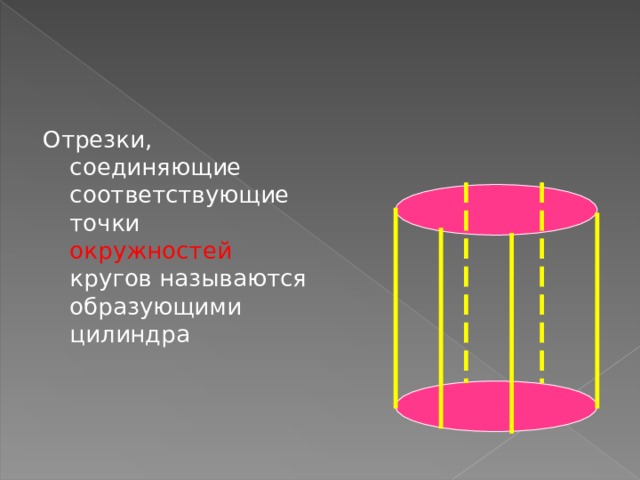
Отрезки, соединяющие соответствующие точки окружностей кругов называются образующими цилиндра

Цилиндр называется прямым , если его образующие перпендикулярны плоскостям оснований.

- Поверхность цилиндра
- Высота цилиндра
- Ось цилиндра
- Радиус цилиндра

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
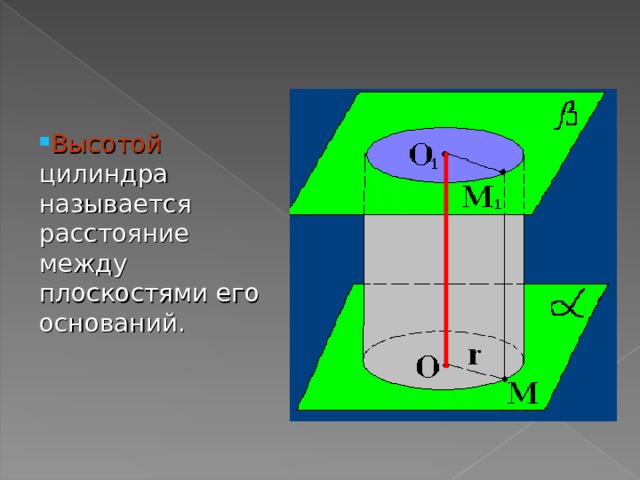
- Высотой цилиндра называется расстояние между плоскостями его оснований.
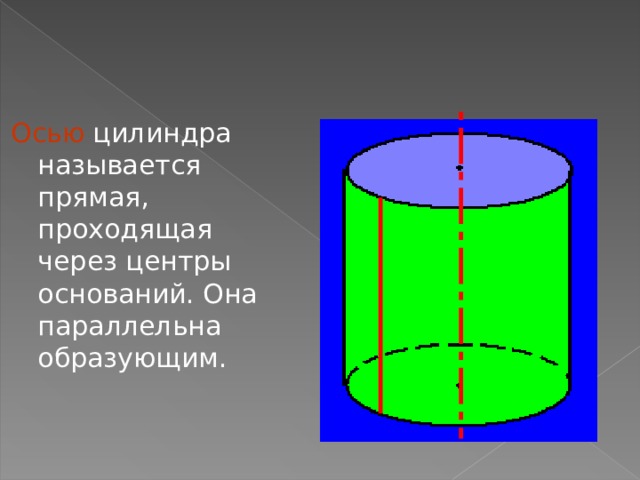
Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
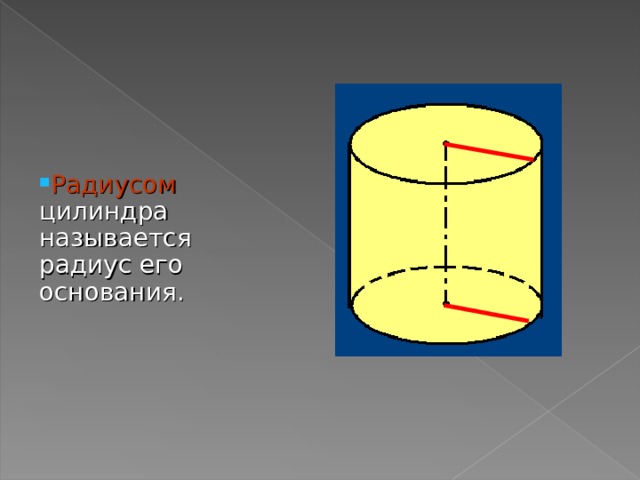
- Радиусом цилиндра называется радиус его основания.

Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
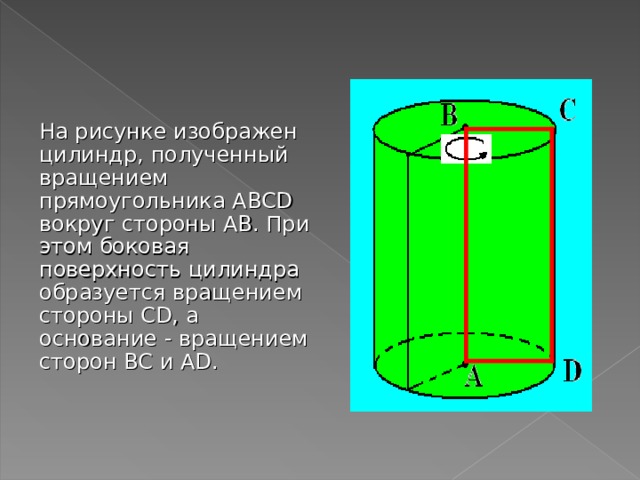
На рисунке изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB . При этом боковая поверхность цилиндра образуется вращением стороны CD , а основание - вращением сторон BC и AD .

- Основания цилиндра равны.
- Основания цилиндра лежат в параллельных плоскостях.
- Образующие цилиндра параллельны и равны
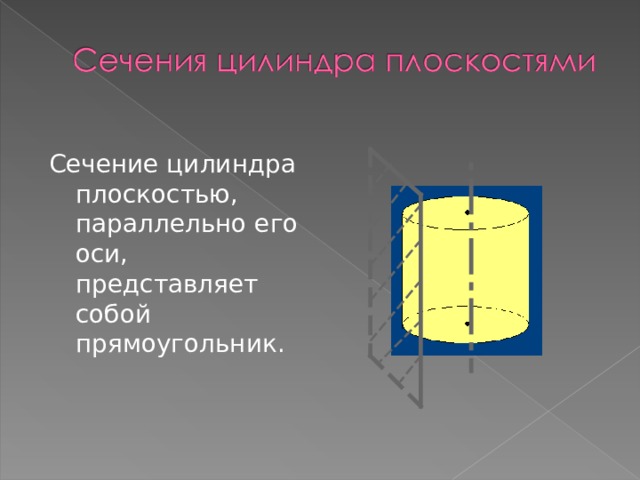
Сечение цилиндра плоскостью, параллельно его оси, представляет собой прямоугольник.
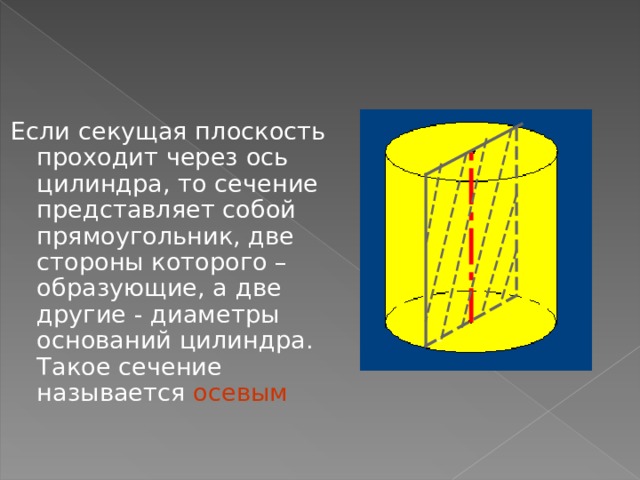
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого –образующие, а две другие - диаметры оснований цилиндра. Такое сечение называется осевым
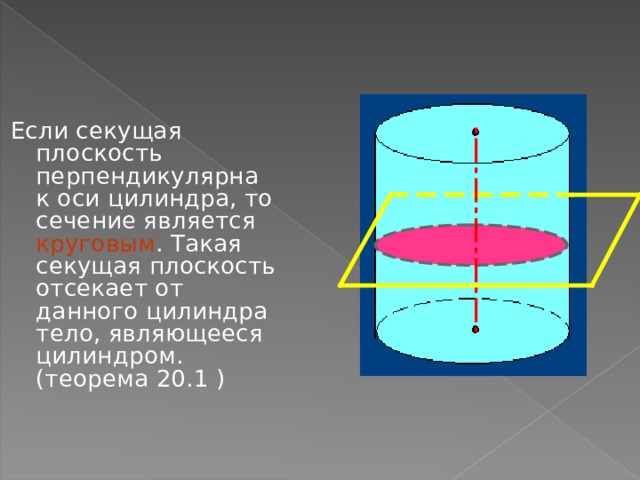
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является круговым . Такая секущая плоскость отсекает от данного цилиндра тело, являющееся цилиндром. (теорема 20.1 )
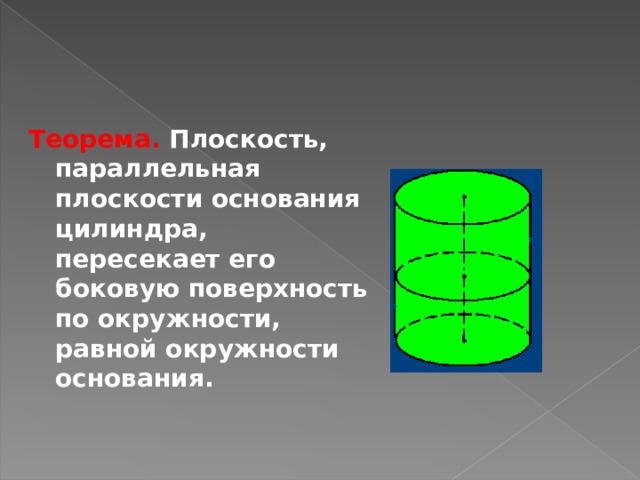
Теорема. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
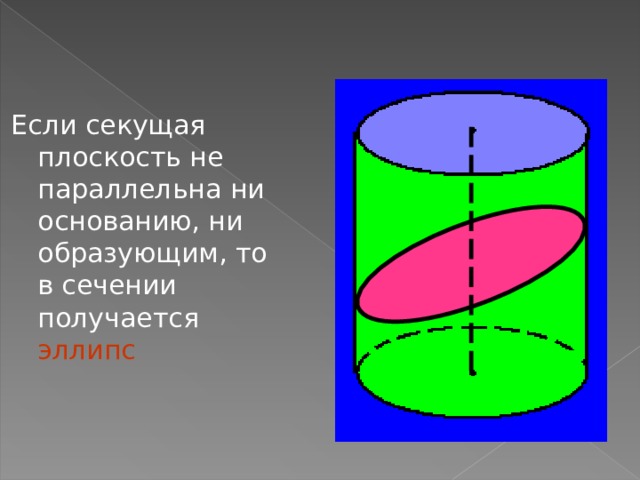
Если секущая плоскость не параллельна ни основанию, ни образующим, то в сечении получается эллипс
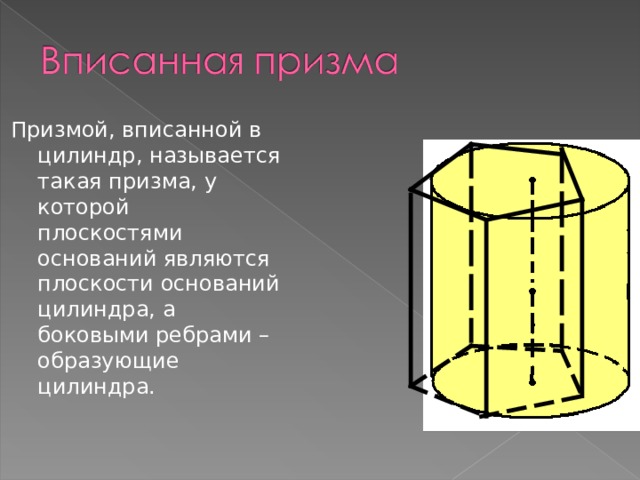
Призмой, вписанной в цилиндр, называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.
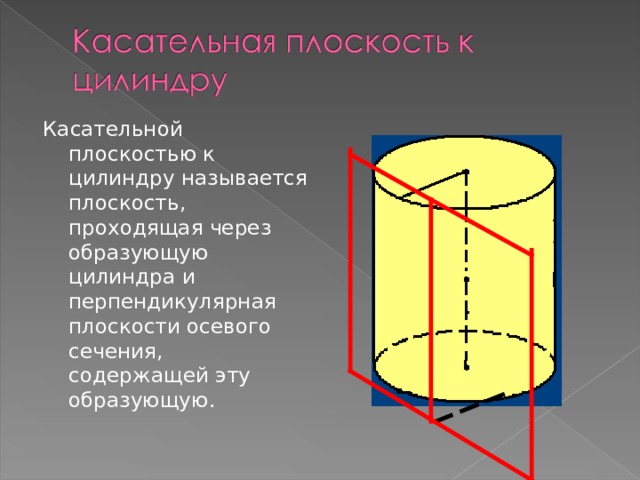
Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
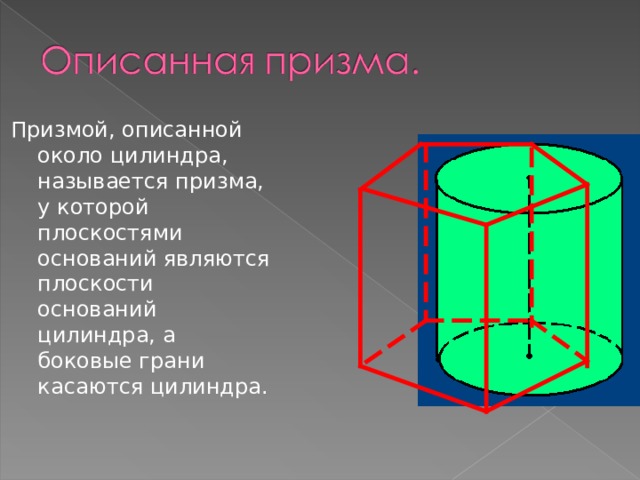
Призмой, описанной около цилиндра, называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.

Площадь боковой поверхности
+
Две площади основания
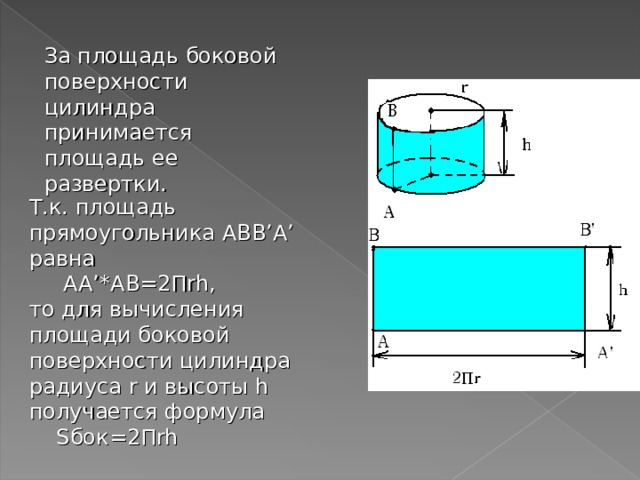
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Т.к. площадь прямоугольника ABB’A’ равна
AA’*AB=2 П rh ,
то для вычисления площади боковой поверхности цилиндра радиуса r и высоты h получается формула
S бок =2 П rh

Площадь каждого основания равна

Площадь полной поверхности цилиндра вычисляется по формуле





